RodriguezGoldstein · August 8, 2025 15:39
diff --git a/pi-estimation.ipynb b/pi-estimation.ipynb
 {
  "nbformat": 4,
  "nbformat_minor": 0,
  "metadata": {
    "anaconda-cloud": {},
    "hide_input": false,
    "kernelspec": {
      "display_name": "Python 3",
      "language": "python",
      "name": "python3"
    },
    "language_info": {
      "codemirror_mode": {
        "name": "ipython",
        "version": 3
      },
      "file_extension": ".py",
      "mimetype": "text/x-python",
      "name": "python",
      "nbconvert_exporter": "python",
      "pygments_lexer": "ipython3",
      "version": "3.7.4"
    },
    "toc": {
      "nav_menu": {},
      "number_sections": false,
      "sideBar": true,
      "skip_h1_title": false,
      "toc_cell": false,
      "toc_position": {
        "height": "887.699px",
        "left": "0px",
        "right": "1533.47px",
        "top": "110.284px",
        "width": "211.989px"
      },
      "toc_section_display": "none",
      "toc_window_display": false
    },
    "colab": {
      "name": "pi-estimation.ipynb",
      "provenance": [],
      "collapsed_sections": [],
      "include_colab_link": true
    }
  },
  "cells": [
    {
      "cell_type": "markdown",
      "metadata": {
        "id": "view-in-github",
        "colab_type": "text"
      },
      "source": [
        "<a href=\"https://colab.research.google.com/gist/RodriguezGoldstein/b6bed79c28e537e89d9071a098dd8f37/pi-estimation.ipynb\" target=\"_parent\"><img src=\"https://colab.research.google.com/assets/colab-badge.svg\" alt=\"Open In Colab\"/></a>"
      ]
    },
    {
      "cell_type": "markdown",
      "metadata": {
        "id": "qNv3hdtkxK2g",
        "colab_type": "text"
      },
      "source": [
        "# Introduction to Montecarlo Simulations\n",
        "Jose Luis Rodriguez Goldstein\n",
        "\n",
        "* linkedin.com/in/RodriguezGoldstein\n",
        "* github.com/RodriguezGoldstein"
      ]
    },
    {
      "cell_type": "markdown",
      "metadata": {
        "id": "45Qtvj4lxK2j",
        "colab_type": "text"
      },
      "source": [
        "## Computing $\\pi$ (Pi)"
      ]
    },
    {
      "cell_type": "markdown",
      "metadata": {
        "id": "aLADm5AAxK2l",
        "colab_type": "text"
      },
      "source": [
        "### Monte Carlo Method\n",
        "\n",
        "https://en.wikipedia.org/wiki/Monte_Carlo_method\n",
        "\n",
        "Monte Carlo methods (or Monte Carlo experiments) are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. \n",
        "\n",
        "Their essential idea is using randomness to solve problems that might be deterministic in principle. They are often used in physical and mathematical problems and are most useful when it is difficult or impossible to use other approaches. \n",
        "\n",
        "Monte Carlo methods are mainly used in three distinct problem classes: optimization, numerical integration, and generating draws from a probability distribution."
      ]
    },
    {
      "cell_type": "markdown",
      "metadata": {
        "id": "MpLOeVwqxK2m",
        "colab_type": "text"
      },
      "source": [
        "### Unit Circle\n",
        "\n",
        "https://en.wikipedia.org/wiki/Unit_circle\n",
        "\n",
        "\n",
        "![Unit-Circle](https://upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Unit_circle_angles_color.svg/420px-Unit_circle_angles_color.svg.png)\n",
        "\n"
      ]
    },
    {
      "cell_type": "markdown",
      "metadata": {
        "id": "ypmX07sYxK2n",
        "colab_type": "text"
      },
      "source": [
        "### Uniform Distribution\n",
        "\n",
        "https://docs.scipy.org/doc/numpy-1.12.0/reference/generated/numpy.random.uniform.html\n",
        "\n",
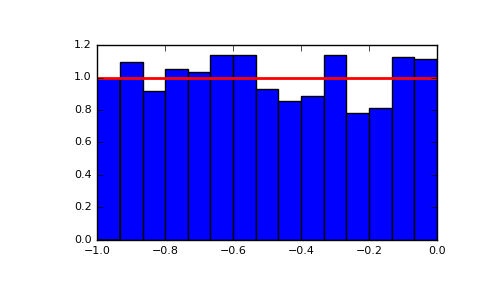        "![uniform-distribution](https://docs.scipy.org/doc/numpy-1.12.0/_images/numpy-random-uniform-1.png)"
      ]
    },
    {
      "cell_type": "markdown",
      "metadata": {
        "id": "6c9My5NTxK2o",
        "colab_type": "text"
      },
      "source": [
        "## Background\n",
        "\n",
        "Monte Carlo methods vary, but tend to follow a particular pattern:\n",
        "\n",
        "1. Define a domain of possible inputs\n",
        "2. Generate inputs randomly from a probability distribution over the domain\n",
        "3. Perform a deterministic computation on the inputs\n",
        "4. Aggregate the results\n",
        "\n",
        "For example, consider a quadrant inscribed in a unit square. Given that the ratio of their areas is $\\pi/4$ , the value of $\\pi$ can be approximated using a Monte Carlo method:\n",
        "\n",
        "1. Draw a square, then inscribe a quadrant within it\n",
        "2. Uniformly scatter a given number of points over the square\n",
        "3. Count the number of points inside the quadrant, i.e. having a distance from the origin of less than 1\n",
        "4. The ratio of the inside-count and the total-sample-count is an estimate of the ratio of the two areas, $\\pi/4$. Multiply the result by 4 to estimate $\\pi$.\n",
        "\n",
        "In this procedure the domain of inputs is the square that circumscribes the quadrant. We generate random inputs by scattering grains over the square then perform a computation on each input (test whether it falls within the quadrant). Aggregating the results yields our final result, the approximation of $\\pi$.\n",
        "\n",
        "There are two important points:\n",
        "\n",
        "1. If the points are not uniformly distributed, then the approximation will be poor.\n",
        "2. There are a large number of points. The approximation is generally poor if only a few points are randomly placed in the whole square. On average, the approximation improves as more points are placed.\n",
        "\n",
        "Uses of Monte Carlo methods require large amounts of random numbers, and it was their use that spurred the development of pseudorandom number generators, which were far quicker to use than the tables of random numbers that had been previously used for statistical sampling."
      ]
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "IlRSe5w-xK2p",
        "colab_type": "code",
        "colab": {}
      },
      "source": [
        "import time\n",
        "import numpy as np\n",
        "import multiprocessing as mp\n",
        "import matplotlib.pyplot as plt\n",
        "from collections import Counter\n",
        "import matplotlib"
      ],
      "execution_count": 0,
      "outputs": []
    },
    {
      "cell_type": "markdown",
      "metadata": {
        "id": "l3HSKP1UxK2y",
        "colab_type": "text"
      },
      "source": [
        "## For Loop Approach"
      ]
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "mDqD1K5uxK2z",
        "colab_type": "code",
        "colab": {}
      },
      "source": [
        "def __inside__():\n",
        "    x = np.random.uniform(low=0.0, high=1.0)\n",
        "    y = np.random.uniform(low=0.0, high=1.0)\n",
        "    quadrant = x**2 + y**2\n",
        "    return quadrant <= 1\n",
        "\n",
        "def pi_for(N):\n",
        "    inside_quadrant = 0.0\n",
        "    for i in range(N):       \n",
        "        quadrant = __inside__()\n",
        "        if quadrant:\n",
        "            inside_quadrant += 1.0            \n",
        "    ratio = inside_quadrant/float(N)\n",
        "    guess = 4.0 * ratio\n",
        "    return guess"
      ],
      "execution_count": 0,
      "outputs": []
    },
    {
      "cell_type": "markdown",
      "metadata": {
        "id": "5v05jho-xK23",
        "colab_type": "text"
      },
      "source": [
        "## List Comprehensions Approach"
      ]
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "BKy3WAzexK24",
        "colab_type": "code",
        "colab": {}
      },
      "source": [
        "def __inside__():\n",
        "    x = np.random.uniform(low=0.0, high=1.0)\n",
        "    y = np.random.uniform(low=0.0, high=1.0)\n",
        "    quadrant = x**2 + y**2\n",
        "    return quadrant <= 1\n",
        "    \n",
        "def pi_list(N):\n",
        "    inside = [ __inside__() for i in range(N)]\n",
        "    cnt = Counter(inside)\n",
        "    ratio = float(dict(cnt)[True])/float(N)\n",
        "    guess = 4.0 * ratio\n",
        "    return guess"
      ],
      "execution_count": 0,
      "outputs": []
    },
    {
      "cell_type": "markdown",
      "metadata": {
        "id": "ncZ5PNWhxK27",
        "colab_type": "text"
      },
      "source": [
        "## Multiprocessing Approach"
      ]
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "qGfa5rdVxK28",
        "colab_type": "code",
        "colab": {}
      },
      "source": [
        "def mp_inside(i):\n",
        "    x = np.random.uniform(low=0.0, high=1.0)\n",
        "    y = np.random.uniform(low=0.0, high=1.0)\n",
        "    quadrant = x**2 + y**2\n",
        "    return quadrant <= 1\n",
        "\n",
        "def pi_mp(N):\n",
        "    with mp.Pool() as pool:\n",
        "        inside = pool.map(mp_inside, range(N))\n",
        "    cnt = Counter(inside)\n",
        "    ratio = float(dict(cnt)[True])/float(N)\n",
        "    guess = 4.0 * ratio\n",
        "    return guess"
      ],
      "execution_count": 0,
      "outputs": []
    },
    {
      "cell_type": "markdown",
      "metadata": {
        "id": "8nm31O-wxK2_",
        "colab_type": "text"
      },
      "source": [
        "\n",
        "# Benchmarks\n"
      ]
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "2OxMFXslxK3A",
        "colab_type": "code",
        "colab": {}
      },
      "source": [
        "num_iterations = 1000000"
      ],
      "execution_count": 0,
      "outputs": []
    },
    {
      "cell_type": "markdown",
      "metadata": {
        "id": "bCGT7S1nxK3D",
        "colab_type": "text"
      },
      "source": [
        "## For Loop Execution Time"
      ]
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "W1-JzEdaxK3E",
        "colab_type": "code",
        "outputId": "78eab504-e0d9-4844-88c7-0183f82e81d3",
        "colab": {}
      },
      "source": [
        "%%time \n",
        "pi_for(N=num_iterations)"
      ],
      "execution_count": 0,
      "outputs": [
        {
          "output_type": "stream",
          "text": [
            "CPU times: user 4.21 s, sys: 21 ms, total: 4.23 s\n",
            "Wall time: 4.25 s\n"
          ],
          "name": "stdout"
        },
        {
          "output_type": "execute_result",
          "data": {
            "text/plain": [
              "3.141448"
            ]
          },
          "metadata": {
            "tags": []
          },
          "execution_count": 7
        }
      ]
    },
    {
      "cell_type": "markdown",
      "metadata": {
        "id": "RZFrTCLExK3I",
        "colab_type": "text"
      },
      "source": [
        "## List Comprehensions Execution Time"
      ]
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "dxn5Xpt5xK3J",
        "colab_type": "code",
        "outputId": "eb61b93c-632c-4598-a3a4-db68c71ff796",
        "colab": {}
      },
      "source": [
        "%%time\n",
        "pi_list(N=num_iterations)"
      ],
      "execution_count": 0,
      "outputs": [
        {
          "output_type": "stream",
          "text": [
            "CPU times: user 4.1 s, sys: 25 ms, total: 4.13 s\n",
            "Wall time: 4.14 s\n"
          ],
          "name": "stdout"
        },
        {
          "output_type": "execute_result",
          "data": {
            "text/plain": [
              "3.137224"
            ]
          },
          "metadata": {
            "tags": []
          },
          "execution_count": 8
        }
      ]
    },
    {
      "cell_type": "markdown",
      "metadata": {
        "id": "ZXKwIfSLxK3L",
        "colab_type": "text"
      },
      "source": [
        "## Multiprocessing Execution Time"
      ]
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "6_wnBgtMxK3M",
        "colab_type": "code",
        "outputId": "b247e866-079f-4258-e2a7-2c98f6800858",
        "colab": {}
      },
      "source": [
        "%%time\n",
        "pi_mp(N=num_iterations)"
      ],
      "execution_count": 0,
      "outputs": [
        {
          "output_type": "stream",
          "text": [
            "CPU times: user 155 ms, sys: 40.7 ms, total: 196 ms\n",
            "Wall time: 1.12 s\n"
          ],
          "name": "stdout"
        },
        {
          "output_type": "execute_result",
          "data": {
            "text/plain": [
              "3.145148"
            ]
          },
          "metadata": {
            "tags": []
          },
          "execution_count": 9
        }
      ]
    },
    {
      "cell_type": "markdown",
      "metadata": {
        "id": "s7DBPld0xK3P",
        "colab_type": "text"
      },
      "source": [
        "# Visualization"
      ]
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "vb8unc9xxK3Q",
        "colab_type": "code",
        "colab": {}
      },
      "source": [
        "import matplotlib.cm as cm\n",
        "import matplotlib.pyplot as plt\n",
        "from matplotlib.patches import Circle, PathPatch\n",
        "from matplotlib.path import Path\n",
        "from matplotlib.transforms import Affine2D"
      ],
      "execution_count": 0,
      "outputs": []
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "EmlODNY1xK3S",
        "colab_type": "code",
        "colab": {}
      },
      "source": [
        "def sim(N):\n",
        "    data = {}\n",
        "    inside_quadrant = 0.0\n",
        "    data['x'] = []\n",
        "    data['y'] = []\n",
        "    data['color'] = []\n",
        "    for n in range(N):\n",
        "        x = np.random.uniform(low=0.0, high=1.0)\n",
        "        y = np.random.uniform(low=0.0, high=1.0)\n",
        "        quadrant = x**2 + y**2\n",
        "        if quadrant <=1.0:\n",
        "            inside_quadrant += 1.0\n",
        "        data['x'].append(x)\n",
        "        data['y'].append(y)\n",
        "        data['color'].append('blue' if x**2 + y**2 < 1 else 'red')\n",
        "    ratio = inside_quadrant/float(N)\n",
        "    guess = 4.0 * ratio\n",
        "    data['pi_guess'] = guess\n",
        "    return data"
      ],
      "execution_count": 0,
      "outputs": []
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "-NVHJUgQxK3V",
        "colab_type": "code",
        "colab": {}
      },
      "source": [
        "data = sim(N=500)"
      ],
      "execution_count": 0,
      "outputs": []
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "dG9YBn1RxK3Y",
        "colab_type": "code",
        "outputId": "86d3cacb-7fd6-4404-b2f9-2398363fa4ec",
        "colab": {}
      },
      "source": [
        "data['x'][:5]"
      ],
      "execution_count": 0,
      "outputs": [
        {
          "output_type": "execute_result",
          "data": {
            "text/plain": [
              "[0.7050070085121255,\n",
              " 0.06921436184555119,\n",
              " 0.6626391483426525,\n",
              " 0.10125124084980897,\n",
              " 0.40860437682418016]"
            ]
          },
          "metadata": {
            "tags": []
          },
          "execution_count": 13
        }
      ]
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "ZFFX8aLVxK3a",
        "colab_type": "code",
        "outputId": "1350162f-1e7b-4113-c69b-9950800b3c69",
        "colab": {}
      },
      "source": [
        "data['y'][:5]"
      ],
      "execution_count": 0,
      "outputs": [
        {
          "output_type": "execute_result",
          "data": {
            "text/plain": [
              "[0.41705161498762755,\n",
              " 0.20219413617113124,\n",
              " 0.9853231265885148,\n",
              " 0.4192147347806826,\n",
              " 0.18937274127117665]"
            ]
          },
          "metadata": {
            "tags": []
          },
          "execution_count": 14
        }
      ]
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "lCt2B5wsxK3d",
        "colab_type": "code",
        "outputId": "26790de6-fbff-45d4-b810-ed203fdf3f42",
        "colab": {}
      },
      "source": [
        "data['color'][:5]"
      ],
      "execution_count": 0,
      "outputs": [
        {
          "output_type": "execute_result",
          "data": {
            "text/plain": [
              "['blue', 'blue', 'red', 'blue', 'blue']"
            ]
          },
          "metadata": {
            "tags": []
          },
          "execution_count": 15
        }
      ]
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "d7VA03iGxK3f",
        "colab_type": "code",
        "outputId": "7d2cc5b2-7130-464a-ae83-a8d95dabc49e",
        "colab": {}
      },
      "source": [
        "fig, ax = plt.subplots(figsize=(8, 8))\n",
        "circle = Circle((0, 0), 1, facecolor='none', edgecolor=(0, 0, 0), linewidth=2, alpha=0.5)\n",
        "ax.add_patch(circle)\n",
        "plt.scatter(data['x'], data['y'],color=data['color'], alpha=0.4)\n",
        "plt.show()\n",
        "\n",
        "print(\"Estimate of Pi:\" + str(data['pi_guess']))"
      ],
      "execution_count": 0,
      "outputs": [
        {
          "output_type": "display_data",
          "data": {
            "image/png": "iVBORw0KGgoAAAANSUhEUgAAAfIAAAHSCAYAAAAXPUnmAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8QZhcZAAAgAElEQVR4nOy9d3RU170v/jkzmpE00qh3oQJCiCIQRTaYYjDG2LhgGxNsgktsJ7aT+CZ+N/cl791XstbLW/fm3vvycu/vpdlx7GA7bnGMwQY3jDCiGJBoKiAJ1HsZSaNRmXp+f3y8OTPSqIEQEt6ftWaJmTlzzt77HPbn27+KqqqQkJCQkJCQmJ7QXe8BSEhISEhISFw5JJFLSEhISEhMY0gil5CQkJCQmMaQRC4hISEhITGNIYlcQkJCQkJiGkMSuYSEhISExDRGwPUewJUgJiZGTU9Pv97DkJCQkJCQmBQUFha2q6oa6++7aUnk6enpKCgouN7DkJCQkJCQmBQoilIz3HfStC4hISEhITGNIYlcQkJCQkJiGkMSuYSEhISExDSGJHIJCQkJCYlpDEnkEhISEhIS0xiSyCUkJCQkJKYxJJFLSEhISEhMY0gil5CQkJCQmMaQRC4hISEhITGNIYlcQkJCQkJiGkMSuYSEhISExDSGJHIJCQkJCYlpDEnkEhISEhIS0xiSyCUkJCQkJKYxJJFLSEhISEhMY0wIkSuK8oqiKK2KohQP872iKMr/pyjKRUVRzimKstTruycURan4+vXERIxHQkLiGwanE6ioAIqLAYtl6PduN1BbC1RWAgMDkz++Gx12O3DpEtfX6bzeo/nGIWCCzvNnAL8B8Now328CkPn1azmA3wNYrihKFICfA8gFoAIoVBRlj6qqnRM0LgkJiRsdra3An/8MdHdrn61fD9x+O//d0gK88QYJXlGAgABg61YgO/u6DHdUqCrQ2QnodEBExPUbh9MJ9PcDoaEcy3CoqADeegtwODj2kBDg0UeB1NTJG+s3HBNC5KqqHlIUJX2EQ+4H8JqqqiqArxRFiVAUJRHAOgCfq6pqAQBFUT4HcBeAtyZiXBISEiPD7XbDbrfD4XAMeXk8Hqiq6vMCAEVRfF4GgwFGoxFGoxGBgYGX/20wGKAoyrWdgKoCb78NuFxAWpqYFPD558DMmfzsjTdISuL7gQHgnXeAhAQgJubajm+8aG4G3nuPfwEgPR3YsgUwmQCbDQgLA4zGazsGjwf48kvg0CGum9kMbNoELFo09NieHq5vRAQJHACsVuC114B/+AcgKOjajlUCwMRp5KMhGUCd1/v6rz8b7nMJCYlxQlVVOBwO9PT0wGazwWaz+f23N3G73e5rNh5B8oLcTSYTzGYzQkNDERoaOuTfJpMJupE0P39oa6NG7q396fUklbNn+W+LRSNxQCOXCxeA1auvfqIThf5+4JVXqP2mplJIqa8H/vEfgdhYHmMwABs2ACtXXv31BgZI1idO8Fo33wzceitw8iTw6afAjBkUGvr6gDff5JpmZGi/7+sjiX/5JRAVRcEpI4PCRmcnUF0NzJ179eOcaujo4DMVHg7ExV3v0QCYPCL3J5arI3w+9ASK8gyAZwAgVZpsJL6h8Hg86O7uhsViQUdHBzo6OmCxWGCxWGC1WuEcp39Sp9P5aNHeL71e76N5C6iqCo9HaOgqnE7nZcHAW0jw/hwAOjo6RhyLoigIDQ1FREQEoqOjERUVhejo6Mv/NvrTRD2e4SZGU299PQnS3/dTzVdeXg709mpCh6Lw/dmzwF13AYmJnNMbbwAHD/KYhAS6EdLTfc/ldFJQqaoiyS5cSOIR8Hh4nqoqnhcgIVdX0xqQnKxp/iYTNe78fI3IXS5q3SdO8DijESgtJYEvX86x32i+cpcL2LMHKCzk/Dweume2br32VpJRMFlEXg8gxev9DACNX3++btDnB/2dQFXVlwC8BAC5ubl+yV5C4kaBy+VCW1sbmpqa0N7efpm0Ozs7R9SiDQbDiFpvSEgIgoODh5D1WNHXB+TlUWnzeIDcXOCee+hGHQyPx+ND8H19fSNaC8T3PT09qKurG3I+s9nsQ+7x8fFIjI9HSGQk/eOCqDweElJHB3DqFMmmsRFYsYKk5PGQEDMzxzzvSUFvLwlCQFXpfzabNYGlt5eEX1cH3Hkn/f8vvQQ8+aQ2n4EBxgzU1HC+DgfwxRfA009Tywa0wD9vASA9ndfr7dXIXcBkAtrb+W+Ph0GF1dXAggUkfkUBoqOBpiZaSQBfK4mwLnR08D6lpY3sd5+KOHECOH6clgedjnMqLua877zzug5tsoh8D4DnFUV5Gwx261ZVtUlRlE8B/JOiKJFfH7cRwH+dpDFJSEwJOBwOtLS0oKmp6fKrra1tWMI2m80+mqr4Gx4eDqPReM380h4P8Je/kB8SE7l3nzxJTnn2WcaQeUOn0yEoKAhBY/STut1u2Gy2yxYGYW0QfwXJ19TU+PwuzONB4oULSDQYkBgWhkQA5q4uKHPnkgSNRmqbn30G3HQTiW3lyqkXjJWcTP++qmoan91O94AQUi5cAIKD+ZnRSBIJCODcBJGfOkWinjlTO3dnJ7BrF/D88zy3CPwbDIOB57daaSIXsFiAxYuBkhJg3z7+ra6mJDd3LnD+PMfU08PPv/c9bcwOB+MYLlzQrpmSAjz2mOZXnw44epQPvhBAFIX37KuvgI0b/a/nJGFCiFxRlLdAzTpGUZR6MBLdAACqqv4BwD4AdwO4CKAPwJNff2dRFOUXAE5+far/JQLfJCRuRKiqipaWFtTU1KChoeGyxi0CyQQURUFMTAwSExMRFxfnQ9h+TcyTgNpa7tHe7uaUFBJ7VdXVK7h6vR7h4eEIDw/HTG8SArV7q9V62TLR3t6O5uZmNDc3w+pwwJqZiTKLhebc7m6EWCxIKClBUng40qKjkXL33QgsKSHp3HILJ3EdN16/SE0lWZ4+TVO2x0NST0jQTB4WCz9P9golCg/nTXC7SaZFRTSneyMykjfQauXxERE8tz/ccw81eBGx3tVFgk9JAV5/HYiPB2bNopWjuJhBcLfdRutAayvw3HMkeIFjx0j03ve0ro7X2Lx5YtZuNLjdmuUgIoLWAVXlmgcHj+0cDsfQ4D29niZ3IXxdJ0xU1Pr2Ub5XAfxwmO9eAfDKRIxDQmKqwePxoLm5GdXV1aipqUFtbS36B/lsdTodzcSJiUhISLj893oR9nDwzu4ajK6u4b/zeMgJQUHc964EOp0OERERiIiIQIZXwJWqqrh40YKCgia0tzdBr29Cz8k89La341JbGy61tSH/4kUoABI9HqQ7nUiz25E6MIDgsW7gkwVFob913jzgzBku1n/5L/RlNDSQVF0uvubM0X5ns5G4xeKaTNTAvSFM8wYD/6an81Vbq5nRm5pIbOvW8fxHj5Kcb76Zws+HH1IICAnhzYyK4o2/cAG44w4S4m23AcuW+V77xAkKI95ITKSv+d57J97EbrNRwGhro/AREkJrRHc31+XSJQp0ZjOtGdu2AfPnj37exYu5Jt6WnJYW+smvs5tgskzrEhLfCHg8HjQ2NvoQt91u9zkmPDwc6enpSElJQVJSEuLi4hAw2C49BREZ6V+JU9WhCqBAcTHw8cfcQ4OCuM+vXDlxysvJkwp2744GEA0gG4oCbLtnOVKP/AFN4eGo7+pCjcWCxo4ONNpsaCwrw9HKSiiKgvj4eKSlpSEtLQ3p6ekwmUwTM6irgV5PDdc71Ss7W/Pzb9tGjV3ciN5easHf/rZ2/M03A6++StO4eK4aGnhOMUedjrneBw/y3ADJ+rbb+N2MGbyWN9rbNVO4Xs8bef48b3JzM7BqFX8/+OZ6PNpnNht9+MHBvg9TQwNN1ACD5YQvf7xobQVefpnBHIGBdKmUljI7ITEROHeOLonaWgofTifN/v/wD76uBH+49VbGENTU8Nx2O7X7jRuvbKwTiKm/e0hITHH09/fj4sWLqKioQEVFxRCNOyoq6jJZpKWlIeJ6Fvm4CqSkUFErL6eCpShU4tLTfa2mAhcvMjA6Pp5KzMAAg371esadXS06O3m+xEQtaNjhAP56ajb+6/xczLtUhHmxsUBEBByJiahbsQI14eGoqalBfX39ZdP88ePHoSgKUlJSMGfOHMyZMwexsbHXPgd+rIiJAe6+W3t/0030idfUULp65BFf4s/KYt73/v187/HQ73Hvvb7nNZl4Xu9zD4eGBppViosZAR8aSsksI4PnfuGF4bXS3Fzgk08Y6NbUxAeno4Of19UBBQXAb36jFZTR64FnngFycigohIYCS5YASUmjj3PvXs5XaM0uF6XItjae3+2m1GmxUDBJSOAxlZXUuEdCaCjw/e8DZWVcj7g4Wk+mgGVHErmExDihqira29tRXl6O8vJy1NXVweOVBhUVFYVZs2Zd1vbCRpP0pwkUBdi+HTh8WItav+02Kjv+9vBDh3zrhAQFcS/Oy6PSeLXWyJoajsHbA2E0Am7ocXHZw1i0agmJx2SCcfFiZMyYAWGUdzqdaGhoQE1NDaqrq1FbW3v5tX//fkRERFwm9fT09KllMZk/ny+nkxq3P4Fj7VqauNvaeAOuJt95/37gwAESYVUVJbTlyylE9PYC3/nOyDdz1SqatsvKSIatrRQKTp5kjnxBAYUB4ffv7QV+8Qs+XGlpvO6RI8DDD5Pch4PDwbF5m76dTgosdXVDNW6Xy/+/R4LRSEFm4cKxHT9JmEJPp4TE1IXH40FNTQ0uXLiA8vJydHr5IHU6HWbOnHl544+Ojr6OI722CAxk5VNR/XQktLUNTUsLDuY+7nTyXFeDkbhDZwzQCM8PDAYD0tPTkZ6ejrVr18Jut6OysvKycNbV1YUTJ07gxIkTMBgMmDVrFrKysjB37tzxm+C7uyl16HQ0X/jL1bsSCH/3cAgNHd+16upoim5sJBneeis/P3CA5pj+fvqWS0pYOe+xx/jyJk67nfP0HpsIMLvzTvqn+/poNWhuZjpXezsfBrOZ2rjDwWv19VH6E3PYvZsa8HCxIzodBRu3W3MpREbyvagb0NamjTEykg+iogzNw59mkEQuITEMVFVFQ0MDioqKUFJSApvNdvk7k8mEOXPmIDMzExkZGWNOsfomYdYsWka945y6u/n+akkcoDnfYOCeL6ybfX38zJ+pfyQEBgZi3rx5mDdvHlRVRWNj42VSb2pqQllZGcrKyvDRRx8hIyMDCxcuRFZWFgJHm0hhIbVRVeXLYKBZY6pVPKuuBv74R2qvYWHUbIuLgaVLSYD5+Uxrc7vpKzGbGZAn0vja22nWLi8nSS5bRt+xyaRFdSckUAhISCCJNzfzO72eJnejkQRvtdLUUlJCEzxAQSIqilLgcP7zgACaekRAmqJQCIiIoJDS1MTzlpXxXCLP/p57pl6p3nFCErmExCC0traiqKgIxcXFPpp3VFQUFixYgKysLCQlJY2/nOg3DGvXMs6osZHKj81Gon3yyaHHikJkFRXcd3NymCI9EsxmWlvfeUezjBoMjPu6mvRkRVGQnJyM5ORk3HbbbbBarSgpqUB5+XnU1FRejoUwGAyYM2cOFi5ciNmzZw81v1ssJPGEBE2L7OtjcNVPf6oFno0XDgfJLiRk4vyzn3xCAo/8uqRHXBzJ+fhxErjDQaI0mxmpbbORnP/7fwcefJABC4pCwlVVmss7O2l2Dwmh2VykzjmdPLdeT8IV+eX9/ZyXw8HzL1pEwlVVEnFb2+i12zdsoLRYUkKBwuOhab+igtfT6Rh539HB9y+8MGXKrF4NJJFLSADo7OxEcXExioqK0Nraevlzs9mM7OxsZGdnIykpaeoEQE1h9PZSwVMUxmGdO8e03ZkzgTVruNd7w25ntc/KSipQdjuDqb/zHWr1I2H+fOBnP6NyBdClOpHB521twEcfheHixWXQ65chO7sXSUmlKC8vQm1tLUpKSlBSUoKgoCDMmzcP2dnZmDlzJoW8S5dIQt6mYJOJJ62uHlvK02AcO0aztjAJr15NP8eV5vUBJLva2qHm5chImlRcLt4Uo5EaeU8Pf5OQQG29sJCa8gMPaL9NTSV5NjUxMOL++4E//YlEXF1N0o6KIsH39fEBsVr5ELhc/G5ggIRrNnOuDsfopVADAynJtbfzfNHRrGKUmcnzeI+vpmZKBKpNBCSRS3xj4Xa7UVZWhoKCAlRWVl7+PDg4GPPnz0d2djbS0tKk5j0OlJZSQ7ZauY93d7OK58aNLBfuj2TPnuX+7W0Ot1qBv/0N+MlPRg+KM5noOp1o9PbS2iyCoN1u4OzZENjtN+Gpp25Cd3f3ZeGvubkZp0+fxunTpxEeHo6lS5diqccD8+iXGRtUlYv7wQeUhIxGEt6BAySvtWuv/Nw6HU3LNpuvT91m4+IuWcJgM5tNiyyPitKECbOZQsvganA6HUkfIGH/+McMcHvjDWr50dF8QGbOBO67j6b63FwS/ZkzjAx3u3mNhQtJxn19o6eJAZyPMJcHB2vjEBDnFb58i4UWhIiI0U1BUxCSyCW+cejq6kJhYSFOnz592e8dEBCAuXPnXjaT6q9Gw/mGoqeHVmOzme5VnY6pYbW1TBG2WFjue7BRo7RUs+gKhIZSEPCnKE4WSkrIGyKWKyCAGv+FC7Qux8eHY9WqVVi1ahXa2tpQXFyMc+fOobOzE3l5efjSbsec8+eRGxCADGHN6e/nicY6KauVFdBOnyb5JSb6Dig5mf7rNWtGl3gcDt6YkhLepKVLtXNt2EDNVacjeff2UqvduJEa94MPMuWtt5cChNvNxZk3j53ZPB7fyG+Phy9v33N4OK9z223Av/0btf3UVPrcLRbmsd93H/DLX5JM58yhVu5ycewhIaOTrHABeK9Fbi5NPmFhmuWisZHpZgEBwPvv0xUg6qcvXkzrwmjBhFMIksglvhHweDwoLy9HYWEhLl68eLkkamxsLJYtW4acnJypV+lrmqGqSkvbFZZTgeBgft/YyH379Gm+9HoqQt6NyNrayB0tLST9pUtpmR3J722z8Tfl5dzrly/3rWJ6Jejo8G/JVRQKLfHx2mexsbG47bbbsG7dOlRWVqKwsBAXLlzAhdhYXMjLQ4TRiGWJiViSlITQJ54Ym/3f4WBb085OErher5ViFYn4gYFcbJdrZLOz08nyqhcvklCdTvq/t2xhXvqiRTzH55+TwMPDWTAmM5Nm77Y2BrYdPUrzSXIyA/bmz+fNi4riOJ1OSmB1dTxnTw9viM3G3547x4dh3Tr+trCQQW9z5zL3/cQJkrvDQXIX69TVxXEOR6719Qy2q62l+X7VKq7RkSO8bmMjg9xmz+b1MzOZP3/sGK+Znq751AsLKZysW8e5NTbyusnJ172C23CQRC5xQ8Nms6GgoACnTp2C1WoFwJre8+fPR25uLlJTU6Xfe4IgCnj19Q3d78R33d30fxcVcX/3eEjwbW3kAoeDe6vdzr199mxqwA4Hfeb+0NMDvPgi9/qICLplCwuZGXU1weEzZlDZHTwPVR0+yFlRFGRkZCAjIwM9PT04c+YMCvPz0VVTgy8UBXkBAZhbXIybTSakpaWN/OyVl9P3LLT35GQSVVOT1u3NYiHxjeY7vnCBJO7tv3A4SH4LF5L8li6lNupwUEAQY3v6aRLiuXMk/pYWEnZEBMmxtxf4wQ9Iei++SIFj2TJ+/+KL9FkfOMCbHBtLwWPXLrZf/R//w7cYgNCmV62iMNDcTOJNS/MteuONjg5WcwsK4lo4nbQefPYZ5zBjBqWu+nqO8emnteCLI0d8G6HodPTpHzlCM9GuXVrUfUwMhRvRG94fGhs5nrAwukAmifglkUvckOjo6MDRo0dx9uxZuL42+UVHR2PZsmVYvHjx1CjHeYMhPZ37ZkgIlUZA+xsVRUVvYIDW3ZkzNZ4ID6fpXbTC7upiwbDFi7kPJieT0wQPDMaJE1QGRTOXsDAqgB9+SOvsSHupw0EeCg0dquxlZfHaNTW8rsvFMdx6KzlqNJjNZqxZswarVq3CpUuXUFhYiLKyMpSWlqK0tBTJyclYtWoV5s6dOzQOw+lk8IDNxgsHBFCLbGzkAonIcQDYsWP0wVy8ONSkIYLXWls1E7tONzQyPDSUOeCiVafLRTP/H/9I039CAiUeu53mce8WqFYrW6oGBmoCSXAwx5Kfzwehro7jyMqilp6Xx4cjI4Ovzk7Of7jKboWFvnWCjUaS7gcfAN/6lnZjU1M14UAQud3uGwQH8HiLBXj3XQoAQUEc35kzFAKWL6egsmaNtqZOJ/DXv9JtITCJHd4kkUvcUKivr8eRI0dw4cKFy+bzuXPnYvny5UhPT5fa9zVERARdi++/z/eVlbSMipbVK1eSyPV6Xz+5KO39wAPck1NTfV3IisJjBlW+vYyKiqGu09BQrdmXP9JVVfJIXh55yWBg6e0VK7SxGY1MlTt2jJxqMjHdbbRKnoOh0+mQmZmJzMxMWK1WFBYW4uTJk2hoaMC7776LqKgorFy5Ejk5OTAYDJQcRL/Y4mL+vekmpkmtW0fJJTmZxHfTTf6lm7o6msmrq/m7oCBKLYPhdo8/cjsggOdNTOT1AWrVb7/NPG5vhIXRhL9gge/nej2D2f7jP0i6isKbsXYtO6J99JFWi91splY/nETW0jLUVeFw8JxOp+/8goIouAjk5FAo8c5Nb2nResALoeb0aT5Qbjdf+fkM8HvmGT48J07QzCSkWYD34LPPGF9wjSGJXGLaQ1VVVFRU4MiRI5d7Vev1euTk5GDlypWImebFHqYTcnOpRJWW8tXeTiJdvpwEWFqqNeLyhsdDheqWW8gR3nA4uO8PZ9GMjOR1vAOuXS7/yqXHQ6t0URG5IjhYK/y1axeVJ28Lrsk09kp2Y4HLFQa3+zbExa2C3X4G3d3HYLFY8NFHHyEvLw/LlyzBTYcOITg8nAvW3c3JHT3KIDGLhQFh20doONnQALz0EgeflETNvbycklBkJCepqjxu9uyRTcX+YLdzAb2DEHQ6Cgzl5TynQH8/iXqwENHXx2M3b9YiHd1u1vV9/nk2MSko4GdLloyc652WRhO/d8Sk0UhCHexy6O31zX+87TYSclERpc3OTq7Z2rU0xQOUBuvqOA+LhYJMQgIf1IsXGfB3/DjH6C2hJiVRANi8+erSA8cASeQS0xZutxtFRUU4cuQI2traAABBQUHIzc3F8uXLYR5sMpOYFERG0sW5atXQ72bPpim9tZX8oapUgBISuB97PLS2VlXxPML0/cADwyuOK1ZQY+7rI3e53dx3V6/2JfLyclb57O7WLMHh4ZqiZzZTiR3OFTsedHVxDAYDlbSgIFrF//hHji8kxIienpsREpKLjRtLUVR0BE1NTTiwaxcOl5RgyaJFWJmRgfCVK2lyOHuWxLJlC00bIyE/n6ZsYaYIC+OiNjaSWEVhlqwsnq+jg76N+nqSz4oVvuTe0aFNZtYskpU/aSwzk4Qm0tj6+7WObUeP0i8RE0Mpq7SUxOdNvqJgS3Ex59zYyGsdOkR/xsaN/uvKL11Ks0l9Pc9vt1P4uf9+Civx8Ry7eOi88/fDw5kX+atf8QFLTyf5nzvHhzM+ng+gTkftXq/nbwCes7mZRO7xDPXNiHUaru/7BEISucS0g6qqKC4uRl5eHiwWCwAgLCwMt9xyC5YuXTp62UyJa472du5/sbG+Vs+gIOCpp+i+FEVcsrI0pUWvB554gvtoSQmVx9zckUuupqVRQf3oI62i5+rVvt0lm5uBnTvJbSkpVLKsVu7Zwj3c3s7rXi2OHgX27dP27+Bg4PHHaWU1GDQXcmQkUF+vQ3t7Np55ZgGqq6tx5K23cPHcORyvqkJBTQ1y09KwJjMToWFhwJYtcC5axj4pIw3AX4OQkBCS+49/zBtjNNJU0tzMgDSPh78pLKQm/OyzJPVDh4BPP+VkFIXneOIJBh/U1PjW33W7GZHY0kIzdEgIBYWbbyZ57ttH7TcggCb5S5eGjl1VuYCAFvTgdjNYLi3Nf/RiaCjHe/gwBQSzmRHw8+ZRIz5yhHO+5RY+GIMlwgMHeKwgaIBChM3GOToclP5U1Tdy3uXSoh6XLaMU6O0TampiIOEkNNyRRC4xbaCqKsrKynDgwIHL1deio6OxZs0aLFy4UOZ+TwH09QHvvUdLp6Lwdeed3D8FYmOB732P0eY63dBYoMBA7pfC/ToWLFzIvdhq5T49eK8uLOT+GxrK/ZhaMZXTxER+p9dTmbsaNDVRoEhO1vZ7q5WZXzbb0PTx2FimU2/erGDmzJmY+YMfoLm1FYdtNhS3tJDQK6sR0J2BglOpaLZyvDt20MLulyOSkxmg4G2O6OsjwYlAM4EDB7SEf4DHtLeTvDduZOnWGTO0C/X00H//9NPMza6u5sK5XJTItm3jxEUlOGHuiI9nwIHDoaV5/epXWqoBQLIV+ekmEwUKk4mSV0QEi8kMJvL2dmriBgP9H4Nbtebm8jUcHA4KM0JoEIiJ4fgfeYSmHKORFoagIApKVqvW1xegkHDpEtddzC8ujtr+JEASucSUh6qquHTpEg4cOIDGxkYAQHh4ONatW4ecnBxZeW0KQfTNED0rnE5Gj8fH0/LqjYn2fAQE+Oaue8Ni8SX3uDju33Y7+QMgwWdk+P/9WFFaynF4W1nDwsh3AwNcD2+3rd0+qEFZRAQSHn4YWz/8EGvCwnCgqgofnFdxqlOFLuJlpKSshM22Ar/+dSCcTvLmEIgi9xYLCbC3l2blRx4ZGjBWXu6bEA9wEUU70IAAX2nBbKYfub8f+NGPaALv6qIgMHOmdv7haqJ7T37bNuDXv6bGbDLxevfcA/z85zyP2UwBoaKCwXKD/eQHD1ILHmwtGEzKIyEgQHMDeD8gvb1axHpfHy0PJ07QdSACNmbM4A0MDORxTz6p5VJGRvJhmqSiMpLIJaY0ampqcODAgctBbKGhobj11luxdOnSqdUj+hsMl4uuyN5eBgCnpWmuTIOBFsvjx4cS+WRi9mxqvpGRHNvcuRx3fz/5IiaG+/P69Vd+jbY2WqKPHqVSPGeO5mrW6WhhOHeO66PXk9Tb2hiQ7YNbbgFmzkR8WRnutSn422/iYAo8AZerEtXVedDrj8NsXkXrnPkAACAASURBVI09e27Cpk2GoQJRcjKjqT/7jBJEbCzzn/310I6M5CKEhlIbbmvT2oq6XP590sJnEBgIZGcP/U74LEaKhu/ro+kiNJSmlL4++kV+9zuO2Wjk2NLTOY4TJ5hKBvC4Y8eY7rVggabRW63AW28xUG64vcFup+Y8MEDhIzGRN/3997luQUF8kDs7qcn/9recZ1cXSTo2loKS2Uzz+0cfaTdQr+eD5h3sN0mQO6HElER7ezs+/fRTVFRUAGD989WrV+Pmm29mio7ElEBDA0tnW63cI0+e5P7t7To1GjWt93ph8WJyQU0N+SE6mvtzRgbHqqokXm8XwHjQ3g78/ve0PIvCN/n5jNaPiCA/PPCAljOvKLzmrFkk//37OcZbbvk6piAhAUhIQHc94AkGoqLmoqGhGv39X8DprEN7+2fo7DyGY8duxx135AxNq0xNBb773dEHvnYtyU9V6X9ob+cksrJ4M73z2AG+F93MBqOmhqH/7e1aSb5Nm/xr5wUF9KWLfO7ubprxLRZKWaKwSl8frxUWRg24oIABFpWVWke0nBxaA8LC6JtvaPCvlTc3A6++quXfqyoX/O67NT98aytv0o4dLI0bGcnzVlSQ9O12ChoLF/IelZZqroDrCEnkElMKAwMD+PLLL3H8+HF4PB4YjUasXLkSK1askD2/pxgcDrpJRQ1yVaVF9tAh+m+FQmaxjB5ofa0RHEy/fGEh996UFFphBelGRfGzKy0zcPgw3aLChSuahoky6I89prW+XruWXJKfr1UDDQggb5SVcZxCVhVCQG0tEBWVjoiIp2C3X0Rr6wH09DThk08+QE3NSWzatAkzhuvTPRJyckhEv/0tLxIZybB9UZo1JobE6G2+fvzxoSbjjg6Wkw0N1TrMFBRQ8/WXKlda6pv8X1fHBbJYeB0R8NDRwTHq9TznBx+QQG02fm82M6I/Lm7kwiuqygIviqKRvMfDGzdnDh/Q5cs53uBg/n37bd+AO4C/r6xk8J6oze4vgn+SIYlcYkpAVVWcPn0aX3zxBXp7e6EoCpYtW4b169cjZBIqI0mMHzU1VN5EAJeiMHNp716akGfOpCaelkbl7HrDZCKprlkz8eeurtYyqebOZcC3xUKF8Qc/8HVDi1atp09rJb4B/ru6msqfyJAKDSW/HD7MtQwOVuB0ZiI0dDbS04ugqp+joaEBL7/8MnJycrBhw4bxpV0qCknsk09ImKGhmvadkMAJ/Kf/5Jt+5k/7PHOGpBYSQsEgKIiSUXExzdTeaWaCLC0WLVBiYIALERGhNV8RAQ/9/dScLRatLWxiohZRCZDwRQSjP2tBRwctAN6auuhNfvo0LRB6vSYMGI0UWkTr1OhouioAfv7pp3zAs7MHBTlcH0gil7juqKurw8cff3w5kC01NRWbNm1ConepR4nrCrebltZjx7i35eRQkxyswUZFMdto5kxaQmfOpHI1Winw8cLlomLU0MBrZmUNH181GYiP53iEFSIsjPu9yeS/YVdHB3lkcOyZ0cg5eac6r19Pt0B1NbksKgpYvlxBYOAibNkyF1Zr/uVyxOfPn8fatWuxcOFylJYGoKaGY1u8eJSysgYDB+vtW1ZVkptoCWqxMACgtZU3NidHI/W2Nmrwp09rtdOzs/mA9PaSyJub6VOuqqI23dREISI0lIMsLtYGWlREaWdggJ9t3swFFoiM5CKVltKk0tzMaz7xxPD+cVXV6tSbTBQGhKVhMAIC6Gf57DNKZcJi0N3N9z09HOOPfsTjrVYGDrpclMi8fUuTAEnkEtcNVqsV+/fvx7mvk3fDwsKwceNGLFiwQJZSnWLYs4cBa/HxJKvDh6nMqKqmtAAkfKOR6cPDlca+WgwM0C9/6ZLWljs8nBlR16uV9OrV5CHRy2RggIS8ebN/XhEVQAfD4Rg6h4wMWn9zczWFsb+fwkBWlhFhYbdjyZIl+PTTT1FWVoaPPvoc//ZvhUhIuAspKZkoLlZw6BBN9sPKxitWsESqd35cYyMrnwEksj/9iYM2mZjkf+wYT2o2c+Lnz/P3ej0n8tVXNE/ExJDoXn6ZkoswvdtsjFifP5/vFy/mBENCKCR0d7Mm7qxZvJ4gXeGTzsriYlVX8+YvWsSHs7+fks+ZM5TuVqzgOS5dolYeGqqVX01J0YLoBmPtWh73wQf0+6em8niTidex23kTHA6m5Anzu6pObDnAMUASucSkw+Px4Pjx48jLy4PD4UBAQABWrlyJ1atXwzjRqpvEVaOjg9q4txk4NZX7Z3Y2CSwggHusw8H971qROMA9urLSt0iMUPaeeOLaXXckpKQw+2jfProcQkJYYntw6XGBxESSc0WF1h1TxFnNm+d7rMnEwOg33ySfAFzvRx7R6r5ERUVh+/btuHTpEn71q09gsbTB7X4TTmcmFi26F7294di7d4T4t1tvpeRRUaFVJJszh58DzCEMCtLM3VFRWqP5227jb2fMIPmGhDAk327XnPynTlG68e6lvmIFtfNHHtEI8vx5dmoLDSWZFxRwUYVg39en5XOL87zwgmbCcDgY0NbQoAkQb77JcSQkcFyiaH9bGx+i4dIp9Hr2T4+JYSGAzExfE4oo5r93L9dDWCfcbgY8zJ179b10xwhJ5BKTitbWVuzevRsNDQ0AgHnz5mHjxo2I9PahSUwpWCz+zcCBgdzjfvQjWjhFAyuxVw+HlhYqe0FBVJTGW4jv9Omh5cFFme+Bgas3sasqX+MtTzB7NvB3f0cuMRhG//3DDzMNWpQUz8piALW/rK3MTOBnP6PwpKp09fpzVWdkZCA19TkEBZ1EdfVBtLZWIC/vt5g37w7YbLlwOBT/bg6Rg93QoBVpSU7WNODGxqE3NiaGUtyqVST+tWspxTQ2UkvPztaIv61t6I1RFC5USIgmkSxcqKXJlZVRY/fOT+/s5O/uu49/Re/yEyf4126nid/bshAayipFd9zBRW5vJ6GbzRzviy/ysxkzqEV712IH+JB6F+UHOF+3m+vmdPreDFGisLxcErnEjQW32438/Hzk5+fD7XYjLCwM9957L+aIykgSUxZhYVrJaG+Ph8PBvfzrTKlRoaqMqcrP19KvzGZqsuNxKQYEDO2EJoj3amoDDQywxsjx4zTXL1zI4mZjaVkqIAK7PR6Srs1GIcNfz4/gYJre777btyX3cAgKGlt/9bAwPQICViA9PRvFxfvQ1FSKs2f3wmAoQmfnZsTHD9tMnWQ2OPrdYOCiO52+0ep2O03bwcF8EAYGKHEIDbehQft3aioX1htuN2/ccP6Qs2f58Hnf1MhIasLR0VzU8+epcYvc9ooKLqQ3kQtitVopWIiHraGB10hK4nkbG4E//AF47jlfMg8LY8W4PXs0CW1ggFGTws/uD5NYaVISucQ1R319Pfbs2XO5rOpNN92EDRs2yJro0wTx8VpcUXIy96eWFv9m4JFw8SLw5ZdaQRSA2v7bb7ME+FjDIlasYC2Q0FBtj29sZJOsq/HMvPsulcCkJJ63tJSu4eefH5/VQJRkbWjQBJabbyZp+xM0Jrqu0apV5La0tFDk5m5DQ0Mp8vP3ITq6Fn/84x+wbt063HLLLWMvaWwwMHQ+P5+ELBqIiE5sikKie/VVSlghIdTqg4K0zjnz55NAa2tJ+k4nteANG4Yv8TecVCYkSrudD0JMjGbGcDgYwLFggWYNEMJCW5s2foBuAe/ub6Ju+hdfsGa8N1as4G9LSijlzZvHB9nl4nytVs2q4HD45iJOAiSRS1wzOBwO5OXl4auvvoKqqoiOjsZ9992H9MEFpyWmPL71LcZCffUV967581lGeqytrCsqgN/8hpZMRaHCI0qq1tRwjx2pU6U3Fi8mwZ44oaXyzpzJmu6jwWajEiaiuZcupTLW1EQS985OSkricWVl4+uI9uGHnI94zD0exoWlp4+/l/l4oKpcF4DXKSkR7u75eOaZmTAYPkNR0Wns378fJSUl2Lx589gzQ26/nSR96pTWIP6++zTf9OzZwA9/qEW1r1qlVcMBKAk9/TQfoHPnSN4bN468sMJHHhWlSX7t7dSCY2LoX3c4fB/CGTMoQJSX8/rt7TSziFSyfftoXhd1dAfXYY+I0BZxMJKShgZ/GAysmvf661oXIJ2O1X/G+kBPABR1ElqsTTRyc3PVgoKC6z0MiRFQXV2N3bt3o7OzE4qiYOXKlVi3bp2syjbN4fHwNR4t8tAh7p+1tQycUxQqQStXcn+uqaFGPt59T1QTNZs1d+5I6Opim26rldp8by/n8b3v8bO//GWoe7ShgfFeYw1ArqgAfvpT7u+xsYw4Dw3ltSMjea1rAbudBdrKyzUrwIwZ5Mq4OE1ZvHTpEj788EN0dXVBp9Nh1apVWLdu3di1c6uV0lBU1LXP91NV5msfOqRNKiKC2nJcHH0Xf/zj0Cpu589rD+jJk/z+ppv42aVL1KC/9z2aYFTVNw+8s5NzG++NEhXfXC5q7teghbKiKIWqqvrtACM1cokJhdvtxsGDB3H48GGoqor4+Hjcf//9SLqWYcwSk4bx+qFtNgZ0paRw/zx8mFbO9naa54OCSHiDg9fGgvH+7vBhjkfEbEVFcRz79tHsLVy23gKB0zlCytYgXLpEQcFiIc/U1lK5W7uWayayk64F8vNJ4t7GrpoaujO8S39nZGTgBz/4Ab744gucOHEC+fn5uHTpEh566CFEjyV3LyxsaIvUawVFodln2TLf6EihDMyYoaW+iRakDgcDz378Y62DjXd6Q2amZhbasIF5jADJ3GqlxLV16/jHGhhITf86QbaNkpgwWCwWvPLKK8jPzwcArF27Fs8884wk8W8wvg6LgMFAcpszh0TX28t9VlUZvX2lZQNqa6mJ/uY3DKTr6hr+2JISjfg7OxkQfeQIFbOGBpqjKypY68Nu536flDT2Zi9793KOaWnkE5FnX1FBgeFaVrc7fnyo1Tcpie6HwTAajdi0aROefPJJREREoLGxES+++CJOnz6NKWmhjY2lmT0ryzfYLiCAtW/dbt6smhpKhw8+yBtht/u3GohI/IULaRYH+Fujkdr+1bbAuw6QGrnEVUNVVZw7dw579+6Fw+FAeHg4tmzZgrTxtBOUuKHgcjEd+KuvqBWGh1ORW7iQRHfhArBuHX3vVxrzWFpK12RoKJWwo0dZA+T739cUNG+IbpX9/Qy6Mxo1s/eLL/I3bW104SYnAw89xBTpsXiD7HatAujixRQQLBZyTFkZI/OXLLmyeY4F/orLiHTwwejuFplbqXjuueewd+9eFBUVYffu3bh48SLuu+++6dPXIDkZ+MlPSMQuF7V0YSpPT6d/3Bui/Kvw44h0N7d7UqPMJxqSyCWuCgMDA5c3AgBYsGAB7r33XgSPNQpK4oaDy0WL5YULtHzabCyOdfvt3Hc9Hpra77vvyknc49E0YFHtLCSEpuyvvvIf+LZ6tVZURVQktVhora2spPn7/vu5p9fX8xpjLfMv0qEHBsgj69fTGtHSQsvuo49eXWrcaMjNpfDgnerd1MR4L4G2NnbrrK3l+1mzgAcfDMKWLVswe/Zs7N27FyUlJaivr8dDDz2E1NEKAkwVGAz+W4fOnk0tvqyMAQouF6WYTZuGugemMYkD0rQucRWor6/Hiy++iKKiIhgMBtx///3YunWrJPFvOM6f5945axatohs38t9ffslAY6ORGqrQmgcGGNX94ovUsMvLR7+GzaYVEfNGVBQtAP6waBFdrrW1vGZXF62oBgNfisK93mCgZn3ihNbxcjTodFqBM1EQJjKSr4ceurYkDtAPP2MG461qa/k3IUGrsCoKnrW3c26pqXQ7v/oq4HYryMnJwXPPPYfk5GR0d3fj1VdfxcGDB+GZAp29rhh6PduRbt3KBzE9naXt1q273iObcEiNXGLcUFUVR44cwYEDB+DxeJCYmIiHHnoIMTHDFJqQ+EahtNQ3aDcwkNrwhQusxrlokeYTdzqBnTtpGY2KooZcXMwiKWvX+j9/Zyfw8ccMZg4Pp9999mzu2729wwenKQqJra6O/vLkZLpQRX/wwEAt2Fmn42c229ibWy1fTm0+L4+mdrOZ8/WnLE40TCYGWldWMjMgOpqWADGfixcpuHh3qouP57pXVTEOICoqCk899RTy8vJw5MgRHDx4EJWVldi6dSvCJivAbaJhMDBYbtmy6z2SawpJ5BLjgt1uxwcffIDz588DAFauXIn169cjYKKrWkhMW5jN1AAFenqYu33mDPtvJyXRhH3nnTRh19RoBKOq1Ipfeom+7GXLfCPT+/qYcdTXR59zSQmbUPX20ora1zd67/MNG6j19/XROmAyUVNdv17TnB0OCgbjqeqm01FgWbGCGr/JdO01cW/o9b6F1bzR2+v/N6rKddDOoceGDRswa9Ys7Nq1C7W1tXjppZewbdu2yTG1NzfTJxESojVgkRgVcveVGDM6Ojrw9ttvo62tDYGBgdiyZQuyrmPKhcTUxOLFTPUSLaYPH6am6HazjkdXF3O2q6u1MtYASeXcOaZx9fUxLSw/H9i2jUHLgNZhLC2NpmOdjlHhxcXUxB99dPRa70lJwDPPsENlZSU5IzNTC4QbGKBlYPPmK0uVDgiYEi2qfSCsFN7pdcJq7t0rXWDWrFl47rnn8Ne//hXV1dX485//jE2bNiE3N/fadCYUXcYKCrQBxsWx/vt4pKlvKCSRS4wJ5eXleP/99zEwMIDY2Fg88sgjY8s7lbhh0NamkXJoKP3LaWlUnLwju5OSSL579tBf29TEfXrBAmrAwcE0/zY1MeZIaO8WC0k8Kkrrdmk0MkBrzhz+rrlZI1edjpUyMzNpHn700bFnDqWm0nf95z9TG4+Lo3XAamU5Ve+iZTcCkpMpYJ06Rb+9qlKgWrFi+Dr3JlMItm59HIcOfY4TJ45h7969aGxsxD333DPxFrhz55hD590gpakJ2L37+rW0m0aQRC4xIlRVxaFDh3Dw4EGoqop58+bhgQcekHXSv2FobQV+/3sSgMVCU7nTSX93ejrTb70JYfFiEuF771FDra/3rYOuKLSaBgXx+64uXkOvp8btXY3M5WIQ2ezZ1CwH997Q6Xju8cqV779Ps7/Ikpw9mwLBypWTQ+IuF4P8jhyhJSAnh+b9a6GAKgoFl6wsdo9TFOCeeyhc+UNFBdvCdnToEBh4J1JTE9HQsAenT59Ga2srHn744Yn1mxcW8gZ6+yLi4zmQ3t6xpw9MNlSVUYM9PRz/lVQ2mgBMCJErinIXgP8AoAfwsqqqvxz0/a8BfB0/CROAOFVVI77+zg2g6OvvalVV3TwRY5K4etjtduzatQsXLlyAoii4/fbbsXr16mtjWpOY0hBVMgMDubcmJZHIOztJhG+9xWJa3vuw0cgiKIWFvt3TRIUzRaE2fccdwK5d1NK7u0mig0twC40/O5vR7w0NJHuXi/voypXjI0CrlZYFbzO8Tkdtdf9+ph+fOcP3d93F0uH+zOyqqlkdQkMpDIzVHL9nDyPjk5IotJw9yzH98Idjr2EvUFpKN0RXl9ZGfLBgo9dTWBBuipHO9corFMxEl9Dy8kXIzY1Fff07aGhowIsvvoht27ZNXK0It3toVSDR03wqFqkB6P956y3eNJG0n5vLAJBJ9u1fNZEriqIH8FsAdwCoB3BSUZQ9qqqWimNUVf1PXsf/HQDv0gj9qqpew1YCEleCjo4OvPXWW2hvb0dQUBAeeughZI61xJXEDYfKSpJaeTk1aNEZ0mIhCTU20uw9uLqYSOWtreU5enupvERG0j+ek0NSDQ8n8bS2UhET2rvFwmNFZ83gYGYQ5eXRGitagXrnS48FQqgYzB0tLdSQDQbOq6qKAXXnzwPPPuvrQnC5aHE4e5Zr4fEw0O+pp/z7nXt6aNqurtYK2GRlacJPcjK/Ky0dX5D1iRPA3/7G9QsJ4XhKSykQjFW46eujILV3L8ubWywU0JYs4TlTUoCSkkS88MIz2L37PVRWVmLnzp3YtGkTbrrpprEPdjgsW8ZOZmFhDFI4d46h9mYzP9+8efwml9EwMEAB4kq1/c8+4wMihBmPhzdjxgz6ZyYRE6GR3wzgoqqqlQCgKMrbAO4HUDrM8dsB/HwCritxjVBXV4e33noLfX19iIuLwyOPPIIo0RJQ4huJmBiSrMejkZ/LRQ1dKB/+Uo4DAoDHH+f+/H/+D3+TlKRpwqJManAwSV9VSdLZ2dy3o6Lo+/ZWcCIiWIXzwQevfD7h4dxv29o0a6jLRbO9otBdIObZ3k4CrqjwNbkXF/Pz1FQtD729nSb773/f93qielxPD9eivp4af0ICBRWB4GAKRYOJ3GolOVdW0hJx8808j9NJPhGpdADXt76e/ULuuGPkdWhvp2WgrIxxZrGxFCzi4jjmY8e06nZOJ6AoJjz66KPYv38/jh49ir1796KzsxN33HHH1VnqcnI4CJHe0NfHwaxaxcm88gpNPlfTp1bAZqPE8nURK8ycSUFhPGZxl4s3PzlZ+0ws3FdfTUsiTwbg3fetHoBf+VhRlDQAMwEc8Po4SFGUAgAuAL9UVfWDCRiTxBXi/Pnz+Nvf/gaXy4XMzExs3bpV+sMlsG4dU8LCwxmQ5nDQDL5kCbVss3n4oKmgIJLAgw9yr/R4uOf19TGHfMECbQ+dP5/abG8vI8tF//Oxor9f61A5GrZsIT+IHhpWK5Uzvd5XUw8K4nc1Nb5Evns3yby4mL+bP5/jrakhCXprw4cPc05CgDEYyCNnz/rWJ+nvH2rVqK0Ffvtb8oZQIuPigL//ewo8/kqKC2vCSBgYAP70J97LoCByZE+P5pKOjKRm3tHB92az6AGvw8aNGxEfH4/du3fj6NGj6O7uxoMPPnjlQXABAcD27VT9W1ooScXGcqHMZpoqLl68+uAFj4dlBxsbKckpCv0ir7wC/OhHY/dpiDaAg4UXnU4rAzuJmIgsR39i2HBOjUcAvKeqqncfoNSvW7N9G8C/K4riN+5UUZRnFEUpUBSloK2t7epGLOEXJ06cwLvvvguXy4Vly5Zh+/btksQlANAM/thj3NzDw7nXJiRoRVMeeWTk1qYiQh3QTMkmE88zOFUrOpqaeULC2Em8uZn55f/7fwO/+AUDtez2kX8TFwe88AL54957WVDFH0+IMtzelt2iIq0fujBWHT/OeXrPUaC0lFYNgZAQ+rKrqrh+bjf9/pGRvmPweNjUpayM65WWRgWyt5dCUEcHr+V0+l7PZhtesBIoK6OAEh8vtG1ePyCA77u6+FeUmr37bt955eTk4NFHH0VgYCBKSkrw+uuvo7+/f+SLjgRF4cOVnExpxlsa0+k42KtFfT0loxkztKo/cXE891hKCgoYjcDcuVpXIIG2tmtbVH8YTIRGXg/Au4vvDACNwxz7CIAfen+gqmrj138rFUU5CPrPLw3+oaqqLwF4CWA/8qsetcRlqKqKzz//HEePHgUArF+/HmvWrJFBbRI+WLCA6V4DAySQ+npqcpmZo+dNp6RQk/fuOd7by/f9/b5uyt5earNjbV1vtZLE9XpqvG43TcI9PSTpkRAURK1WYNkykmtHBwna5eL558/3Jdj9+/m+qIhkGxjIvydP0vIwOKBb1Jz31pznz+f5+/tJmjk5rEfvrRR2dGhlX4XAoChas5eyMga2ff45uS8oiAGIHs/ocQNdXZrwFRamxZQZjewjIrht9mwKOrNmDT3HrFmz8OSTT+Ivf/kLampq8Morr2DHjh2IuNLQ+7g4DkSYbQC+d7tHl0zGgt5e/1V6ROrEeHD33TRp1NRo0k9qKnP6JhkTQeQnAWQqijITQANI1t8efJCiKFkAIgEc8/osEkCfqqp2RVFiAKwC8K8TMCaJMcLlcuGDDz5AcXExdDodNm/ejMWLZeyhhH/odNQMTSaS81ixdi2DxtraqPX19pKknnqKEeIGA5Wx3l5q1488MvbWpkVF1L6F2ToggP8uLtbKlQIszXrqFAl+wQIS+GBh4aGHeK5PP6XiptPR9P3972vCiqpyHrNm0T3gHbQM0GQ/GGvWsI58cDCJ0u2m9r5jB1POhoMIohsMj4ekbbeTTwIDuY4tLVQ2t2/3H3DnjaQk/t7l4j1JSSEnORwcY1gY3dKbR8kjSkhIwHe/+1385S9/QWtrK15++WXs2LEDiWNt5O57MkZ+nzjBGycCD7KzR6/0MxYI3463oABw0t7+7rEgKgr4u7+jNGWxMDdy9uyRTVPXCFd9RVVVXYqiPA/gUzD97BVVVUsURflfAApUVd3z9aHbAbyt+ja8nQfgRUVRPKCZ/5fe0e4S1xb9/f14++23UVNTg8DAQGzbtg0Z07AXr8TUR1ISyfCLL+jujI0lQWRlkRA//VSrt759O/PQx4q2tqE+YkXhPi3SewsKGNktiFQEqj3+uC+Zh4TQxL51K2MAhCth8LnT0jQteuZMXsdmo5btHbwmsGAB5/v551r63a238jUSoqJ4ztJSkm5gIH8/MEDOW7BAKw27ciVJebh4MI+HVhSbjRaP8nIKV4cOkcTnzKFSKdLoli3jte12/iYsbHgrSXh4OJ566im88847qKqqwquvvopt27Zh9pUUmr//fvrICwo42SVL+AC1tY0unYyGmBjgllsYtBATw8Vrb+fkZ84c//mCgkbP55sEKFOykfwoyM3NVQsKCq73MKY1enp68Prrr6O1tRVmsxk7duxAwkSYriQkrhBX2hL69GlmKIl67eJcDQ3Az35G8vnlL0no3iEfVVXAt79NM/Jw8HjIJ19+SVNzVhYjwUXN99BQElx3N03kzz47sqXCbqcAYDbTqjEWdHUB//7vFIJE2lxqKvDAA2PvrGazMcarro6/LynhWq9cScvA+fN8/5//Mz/T6Tj3vDwSvcfDddy4cWTLscvlwu7du1FUVASdTocHH3wQC0da4JHg8TAkPz+fg1ZVEu62beNPtB983nPn6AdxuEtGrAAAIABJREFUOCgo5OZOTET8NYSiKIVfx5MNgazs9g1Ed3c3du7cCYvFgtjYWDz66KMIH6x2SEhMMrxJXNRdP3iQRJaZSf+xP4Vs/nxqp7W1VLKcTipZontac7OWKueN0FCmlI3EM19+yU5rMTG0nFZVMY3s+eeB557j942NFCLWrRvdOhsYOH6lMiIC+J//k1aC0lIqgQsX0iogFEq3m/NuaSHHZWT4znffPo4zLY3ui/5+rUqfaLQiXAlCMDh2jBaElBSSuMPBwj1m8/AV4QICArBlyxaEh4fj8OHDeP/99+F0OrF06dLxTRrgA5CX59s8pbyc5psHHvA91mLh8V1dNPHMnTs8Met0NPncQC5ESeTfMFgsFuzcuRPd3d1ITEzEY489BtNYVQMJiWuE/n4SCUBt88wZ9tCIi+Pr0iWS7vPPD60LEhgIPP0003fPnaN5PCyMbtaDB0lwHR2ai9XjobZ+9iw16TlzKAwM1mwHBhgx3tREU3xgIPkhIIBa+saNjOS/lqiuJqF2dvLad9+t+eotFo6vtpb8ZrFwHmFhfD31FNduYIBxBELI6O/nXIODKZiIdQkO1oKwVZVCinfwuNFIgebQoeGJHAAURcGGDRsQGBiIL774Anv27IHT6cTy8VbtOXaMF/SW8GbMoE/k7rs1oq6uZmN1EXUoarY/8cRQ6e0GhSTybxDa2trw2muvoaenBykpKdixYweCrqS9k4SEF9xuanuqSq11rNHmAuXlwJtvailUej19uTExNGGbTNRiGxpI1vfcM/QcISHU2G+/nQpbXh41yLIy/q2qorZ6zz0k5YsX+TujkUFoq1YNDeo6e5av5GSSp9NJDsnK4viuNc6eBd5+m9cODqZp/fRpWgKCgoDXXqNvXuR/R0YyzuCOO2hK/+tfgR/8YGjKs3eGgXcgXV+fRupuNzX3wUJTcLAWFT+SPx4A1qxZA4PBgE8++QQff/wxnE4nVq9ePfYFsNspNfX0UOIKCOCA3G4t0MDjYQWe0FDfYIaqKkqD4xUepikkkX9D0Nraip07d6K3txfp6en49re/DeMU9wlJTH00NLAlaXc3icJkYsS5v1Qlf7DZ+PvISP7W46EmePgwU930eu7RK1dyn66rG/l8djtLnwYHa7XS9XpyQGsrC3r19FBTXbqUJnmPhwLC8uW+Zu/CQo5JBCGLyPqSEv/CxETC5WIufEKC5g4ODaX2feoUzd1tbTSVHz/OY4KDqW03N9MaXVND0o2Koqm9oYHzCwqiFeKrr+ga7u+neT42VkuxCwjguUX7WYOBY+no4O//5V947+LjqRwPF9O2YsUKGI1GfPjhh9i/fz/cbjfWCp/HaMjJoR9DPFwiLe2uu7RF6eqiKWJwRHtUFM0Q4yHy5maWGayr4wKvWjUxKW+TgElsey9xveBN4hkZGdixY4ckcYmrhsNBrRDgpp+aqmmKNtvYzlFVRU1XeHfq6zWyEEVYBgaonfb0jO6D7u8n8dTX+5aPDQ2lJh0TQ3646y5tjxZ1QVpafM9lsdCEbLFwrqpKQcHppBBwLdHVxbkMjukKD6eLYWDAt6+4261p16ItrDc2b6b2XFOj5f/feSd9404n0+O++10t+l9o8IcPU1A4fpxR/xUVtL6I4jR2O4uijSRgLV26FA888AAURUFeXh4OHjw4tkWIjeXiezxauT1VpalAVTlR8cAMrv7jcIyvhnp9PfC731FKA/j3d7+bHNPLBEBq5Dc4WlpasHPnTvT19WH27Nl4+OGHYRiv7VNCwg+qq0nY3g2wQkOp3VVUjK3A1eAqlzU1DKaKiiKZBQZSOywtJXmMpmCZzdy/e3p803n7+qiF9vWRrPxFeg8OFZk1i3yxbBnn093N899yy7XvVmkyaZ3ivF3EYh6JifyupITuA9HMJiiIAorIJxdFZGJimBNeVsZ1TUri/IbLErh4kXEJmzfTCtDdzXtRWcky4kLACA8nZ+bnMwNgOOTk5EBRFOzatetyS+R169aNXHSqrIymGBGVFxrKibe00MfwySda4YGSEvpVEhMpmfT0jF7vXFVppujqYlRfUJBWfs9k4oP8+efAk0+OfB6AC1NYSOkrO5vRiJO4z0oiv4HR1tZ2mcQzMzPx8MMPX3ktZAmJQfCn+QEkoNHKowqkpfF4UYQEIEGJSmmFhdyTg4MZZPz++yyiYjb7P59ezypk589Tc0xIIPkFBpLUBAGKZimqSpN7dLRv+hrAZiEXLnB/X7NGq0P+rW+NbW5XA5MJuOkmmr9nzCBJNzWRYDMzyWsREczO6u7mGPv6tMwqgL50b4wn5bmoiLwZEaHVjHc4uB4Oh6/QExo61JrhD4sWLYKiKHj//fexb9+XOHlSh+TktcjI4LiGZJSpKskwNtbXFONyMcovJkZLJzh6lKS7YgUHt3kz/QnDYWCALUgrKijV5eVRQoqI0CTAqCgS9Gg4coR+kJAQjre0lCakxx6btOIwcle/QdHV1YXXX39dkrjENYPoOeF0asqH2839dzApDoeICO65u3fzXEYjzbRGI7W9sDAeoygamX344cja38KFwH/7b8C//iu1ycRE+nLdbqYgm0wUCGprOdZZs1hWdfB/j8REBovl5/PY9HQWcBlPRburwaZNFExEDfdLlxg3UF5OP3ltLU3/JSWaL31ggOPz9q1fCQyGoRXlAgJ4XwYGfD/v7By7gLBw4ULU1yv45S//BiAP2dnBKCm5GcePsxCPj1Vk0SKmB0RHayaUzk7NjCDq4BqNzP0rLeXf9etHT9LPy6NUJB5U0e0mOpqEDlAyGq11am8vLQMzZmj/CUS/34sXmWowCZA7+w0Im82G1157DVarFWlpadi2bZskcYkJR0QEyWbvXu5hQrudP19rBDKWAi8330wyrajgb958k5HlVVW0VEZGUgutqeG+WFqqdegaDllZwO9/Tw2yspJjXbRIMzU/9xwtqqJPx3BISJgcDdwfDAYG1a1cCfzjP5IrRJOUmBhahZOSaNUQvNXfz9/p9bwHw9XA7++nYGC3k8MGx3QtWsTsL5dLE3AsFro2envJpyEh/ExRGBc2Fng8wPnz2ViyxIFLl/agtnYfliwJQkvLIhSc8ODWWfVaOb7Zszn5r77S/C8hIcz7+/zzoScPCeHCjEbiqkrpyLvNXFYWF7esjETe308zw44dI59LmCIGm9GDg7nAksglrgQDAwN44403YLFYkJiYiO3bt0ufuMQ1w6pVJJLDh6lVA1r76NRUlkAdS5kCYSUFqG2eOkWhQFWpAQr3pcvFz8bSKdJoJCEtWuT/+yvt6zHZOH6c5vKYGBKhKPqiKFwHu11b44EBrbHXcPOrrwf+/GdyFcD1XLOGAYCCL9PTGY3+ySfa76KiqDV3dzOzoLWVPLV2rW8znJHQ0yPy3ZciMHAApaWf4cyZD5Cd4Yb6+6OA8SsSqigj9+yzDK1vaNCa1judwIEDQ/0xqjpymVXx4AQEDK21npLCCMYzZ2jqMJlYgcffw0NphJXhOjpI2N3dXPzYWAoITufIEuIEQxL5DQSn04k333wTzc3NiI6OxqOPPirzxCWuOZqbWfGroYHWzt5euirr61mQ5e67aRo+fZob+dy51NqHky/PnOFvExK0hlSlpdTabTZqkNOhEGFXF+crcuGTk8dWTtUbHg8LsBgMXMO+Pn5ut3MNAgL477Y2rb68ojCX3N9/fWHxCAzUyNft5jXmzPF1K69ZQx5rbOTxqam8Xmzs8OlmoyEwUAviy8hYCYejHxcv5qPq81+i39kPZLi4WE4nE/xDQoDvfMdXew4Koj9m1y5twi4XsGHD8GXzTp9my7quLk4gJoYLOmOG7+BeeIGSSXDw8Oakffvob4mMJJEfP84blJVFv9D583zAvdvqXWNIIr9B4Ha78e6776K2thZhYWF4/PHHETKe9AsJiVHgcnFTVxTuq3o9A3vffZcKSUoKP7PbubetX08XZ2oq44oMBipQZ86QCAY3LAFI1BUV3GcHBvhyOLjx19WxWtuvf3195j9WNDczVevIESp3kZHc42fOZPzT4BanI6G3l39tNr6EAKPTUXBasIDHOJ3ksNxcppUNV3mtpYX3yjvTQK8ndxYXD40PCw+fWKEpKIhZACdP8nmZO3c9+m096D/+MQ6H2LAoKAtJQUFaasE77zAgYnC6bG4uJ1FWxocjM9OX7EVEY0AApcK336ZkmJbGB6migkJCby8n73aT1G+7bWQTUns7A+uE5n/yJAm7qooLazJRWFi6dFJNPpLIbwB4PB7s2rULFRUVMJlMePzxx2XtdIkJRXU1NbneXhK52Uz/7TvvcF9raSH5pqZSsRFtSnU6rdSqCL6KiWEcUEnJ0HLX/f3UQrOy6N82mUh8IpJ93jzuwZGRmit1PMQ4GKpK4UR0E7ta2bevj26Fjg6tTklPD7lEBNl95ztjP19QENfDbOZfQewiNQ/gfWht5fmfe27kOQyX7SWasVwpqqv5HHR1UbNfvnz4zIJNmygUnj4N6HQKEuPvQmLMv6HR48YbVVV4KiMDMUFBJGG3m4vpryVqbKz/PMDqakqXVisnduECcyGFtFJRQWnTaOQC5+ZSupg1a/Qo8+ZmrSC9zcYHNiqKQoDZrOW4f/AB0w4mKTJSEvk0h6qq+Pjjj1FcXIzAwEA8+uijiBHORgmJCUBvL7BzJ/cp8WhZLMBPf0qCNpupWdfXUzPMyuIxra2M8i4tHepDNZupTA0m8pgYmqCtVhJXYiIVnbY27sMXLlAAWLJE69C1Zg3dqeM1W3d1saqcsDK43Rx7dDS12+zssXcoEygv5/7e1aUpleHhXK/AQHKI1Tp24cNgICl++SUJUrQU7eujVUOv5zEi6PrsWcaHDYf4eM6vs1Nrt+p2k4+utEnZ2bO0uJjNFNa+/JJWl+ee8x9sFxhI9/PGjZxHVFQQ9P0r8Pa+fahwu/FaVRW+O3s2wnp6hkpXHg8XNyDA/yJ2dzMAwGymFOV2M4CjqIgTFFKgqmqLeOkSBzSWgOCQEJ7TYqF2LswkFgsXNTWVN8XlAl56CfjhDyelOpys7DbNcfz4cZw8eRIBAQHYvn07krzNSxISEwAR3ey9KTscmrsRIFELgqiupha6eDGzgVSVL284HP41NkUB/v7vucdarSTZ9nZeOzubhF5ayr04JYWKUF4eiWO8eO89njstjfMoL+fee/AgA/f+3/+jMjgeiEI0bvdQwcLp1Ny548G999JX3dnJ+2AwcO46nW96dUjI6IXIdDr2e/d4SPw1NbQ03377lbXjdrmYtZCYyDUMDeXYurpYA2AkhIWR44xGQP/ss9iWmIhUpxNWqxVvFRfDATACTxB2bS3wH/9B38q//AtLCFqtvictLeWgxMOl12u9zCsreXN0Okou0dFctP5++inGgqQkHrt3LyVKq5V+pI4OTlwURcjO5o06dmw8y3nFkEQ+jVFRUYFPP/0UAHD//fcjfazJuxIS44DdPtTsKnKJg4O5Z1mtJNeICG7OP/858Mwz3PcyM7n3qSoJrqqKilFgoP/CMStWAC+/zIh4j4e/X76cx7e38/yCsPR6EsjRo+ObU0cHBQ5hsRXW1pgY7utpaZyjvyynkZCcTMJOStIC04QQo6rUiIUmPFYYDEw/W76cvu9Fi3iNhARft3Bfn38L9GAkJgI/+Qn99du28d8bNoxvTALd3bzu4Jz1iAiu6ZgxZw4Mv/sdHrnzTkRGRqLJZMKuefOgZmdT3f/DH4B//mfepJQUar6VlfT3eEuJfX1Dg9Tmz+fNtFpJ8jYbyVaYjoCxm3OKi2lKnzWL/yni4yk0OJ00XfX20lwUE0OpprFxHItw5ZCm9WmK1tZWvPfee1BVFWvXrsXCK7WLSUiMgtRUjYTFHik27ogIasWJiVR6WlpocvdOn926ldpvSQktnP393FsPHKAm/fTTQ+OCMjOBX/yC+6LDwd/YbNwz4+I0kgRIdCKVaqwYrBXX1fHc/f1axbr4eI5ZlJEVmUsj+ZLT00m2Z89yTvX1PF9aGn+7ZcvQ37e00PpbW0tBYPVqX4IG+Puf/ITj6enhdUSdekXh2gcHj70wi9E4MSnOJhPvS1kZ70N8PJVcYbUeF+bOhen//l98u7ISf3rrLZwvK8OBf/on3L5oERfy7FlOODeXxJuURJNCU5O2YOnpjE73dvpHRTH4LCmJpfDi4vgARkbSdBAePnoRf4FTp3isEA5E9bk33qAJyrvvq9VKP/kkQBL5NERvby/efPNN2O12ZGdnY926ddd7SBI3MOLjGcx74AC1YtE85PbbtVxv8brzzqEEERrKAK+//pWkNneuJhA0NnJv3bZt6HVnzKByYzBQiBCxSpWVvum9bW3MGBoPYmJI3KJoitFIoh4Y0DhBtOksLqZmbrHQGrtx4/CZRTodu7/Nn0/Tcnc3f5OdzUC9wT7jxkY2+NLrySdlZRR2vve9oQ29wsM1/7fLxaj4w4dJmgsWMOXsagL/rgRHjnAOIvVQUTj3wMDRS537hU6H2Nmz8a2778ZfPv8c+WYzovv7sTgggITc0EBt2Gjkw9faqlXGAegfyMmhhCgK/1utjAjcsoWpFB99xM+sVj4Ejz8+tspFX4/vsgXAu8PM3LmUAoVEKSrlTFIbVUUd7LyaBsjNzVULCgqu9zCuC1wuF3bu3Im6ujokJyfjO9/5jiz4IjEpqKmhC1KnI3HEx1NBKSjgZ7m5JN7hYob++Z//f/beO7qt80wTfy8aC0hA7L2LRRJFqtKyKFHFapZsWbbl3uI4jmPH6ZNkd39zZuZMZmdnZrObzWySjTMZO3ac2I7jIsmWY8kqVKEK1ShSlEiJvYJgBUESAAHc3x+PPn8XjQRIiKSi+5zDIxLl4t7vQt/z1ufF3sqqrYl4W9n992PvVSrhxBQX45iVlaj0Dg/H+zo6EBJfuBCPjY3hPF54wbeKmS80NqIuShTh1NXUgGxLSrAHt7QgMlBfDycuIgLE39MDwyQYHu3vfw9PXFp8zQyGF1/07xju2iYzhc5Ool/8AhxaX4/1ZFPifvpT/6MDXlFbS5U//Sl9ajSSUqGgZ3NyKOPqVVyoTscFBoaHYd089hgqz4nwpbp4EdJ+Q0P4guj1qBZ88klYa+3tsBAzMwMbbnLpElrZMjP5ond14e8VK1BgMTCAL8769b772qcAQRDOi6K4wttzskd+G0EURdq7dy+1tbWRXq+XVdtkzCgyMlz7j4ngcPjrdDDPWgq7HfoZDgcfYvLeeyDRXbtA6nFxMBbMZuyNOTkgDqMR6VLmAQaK7Gyi730PxsnQEHigtRUE5XTCKOnq4ulOIvzrcCB6Gwwib2z0rOiPikLY3N+WsNkgcSLkwJVKOMeFhUg52+1ceW5aCA+nlUlJ1BsRQWeamui9piZ6cd48irp+HR/AppytWoXQxZ49IOrISJxUezssDOmXs64OxWfr1vHB64Fi8WLctHPn+M2Jjyd64AHkUnw18N9iyER+G+H48eN0+fJl0mg09MQTT1BEoC6IDBmziNWrifbuRfST7YFXr4IIpEIkkZEQflm9GntkZqbnEJa77w7OOUVFueqEDw7CI9br4RX/7d+6in+x8wtWDVNMDOoApCFxNqtjOn3dMwGmry/9W63GefsbqfaJ9HSi+HjaqlZTn9lMN4xG+qPZTC+kpVGoxQJPNzPTVZ6upQUWhdOJUJF7oUFiIr5YgeZhpFAqEaJfvZo372dmztiUM1+Qifw2wfXr1+nw4cMkCAI9/PDDlDgDvYkyZAQKphwWFeWp1VFSgtD4xYvYD51OpD3dtYuY3kZPD0itthaPL1rkGREINtjYTtauzPrYpZXmg4Oe+eupYuNG9Oir1Xx6WXc38uzBhtPpKn4zXT8gPx9qpUwLn4jrpUxbB0WhIHr2WVJ8+CHtHhuj/+zoIKNCQR8tWkSPKxQkeOvQ8cd6cB/p5gsmEy+E8yaulZg4I/3h/kIm8tsAQ0ND9OGHHxIR0caNGylf2jYhQ8YcgM2GYrYrV7hQy9KlruNBVSpMElu3jnu9fX3oLnKHKILwa2tBEqIIeevNm0F+txJ1dYgcDA3hp7sbEdWYGPxtNqMXOxhYuBCFfgcPctGbhx/2FMqZLoaGUFjNxG+I0KK9Zs3UjxkTg/v5wQdYk2vXYHgVFaFbbPduT6c4IERFEb3wAoUODtKT/f302nvvUZ3JRKe6umh1QgKP35vNyK0wclco8OW7cMHVojAY8AWaCE4n0WefIQQvCPj7rrswMGAOT5Ccu2cmg4igof7+++/T2NgY5eXl0Zrp/M+TIeMWobwcJJ6Rgf1PFFG1nZTkSRbx8TwiGhUFQjcY8JgogjgjI0HiTCjL6URh23vvob4JOt2BK69Nhs5O6IzExHBhMKcTBodKhTD7+vXB88iJkJsvKkIv/MWLGGAyPIz0gb/X196OCWmstS8vz9VBlYrfECG9/OmnINrs7Kmfe3Ex3v8//gfqu/LzsU4DA0RvvIEahGnfo3nzKGrePHrwoYfonXfeoS+0WkptaqJ0pvgWEkL09NOuifnNm3Ezm5v5Y2ws6kQ4exYWY0YG/+JVVCBMU1Y2zQu5dZCJfI7j4MGD1N7eTnq9nnbt2kXCXE+cybjjIIpwYJKTubcnCCDxU6dA5OPjrj3YoshrjxwOENfwMELMixaBMP/yF3j6tbUo/uruhmfZ3w+i0mqJvvrV4EY4KyuRs2dhZ6USadfOTqLvfGf6Wuy+sH8/1iI+Hmtw+DDW58UXJy+qrqzEIDCNBq89dw4E++ijcE4HBlCfJTU+1Gpcy4ULnkTudMKgOHUK679kCWrKfBFyby/uq7TOKyoKHFpfH7zoQn5+Pq1evZoqKiro/ZAQ+sa2bRgMlZHhWe0YEYERqM3N+NJER+N1k1UGnjiBLxSzgli/+vHjMpHLmBpqa2vp9OnTpFQq6ZFHHqHwYLsfMmQECePjnilKpZK3KHV1wcveuBGV6MePwyOMjsYerFZ/GUmlqCi0grW1oZvHYAC5WK04RlcXb236+GNoegcL/f2ehMWua2wseETudKKTqaICIfW6OleyzMgAB12/PnGB9ego0b594Bo2ICw2FtopK1bACWXiN+4+ABuBSoQ17etDdOTiRfSHx8XhNV98gbC5L6PClxiPUomodzBxzz33UHt7O7W2ttKHNTX01FNPkcIXOatUgavSjIzwgQIMGg0ucrqTZW4hZInWOYq+vj7as2cPERFt2bKFUt1LZ2XImCMQBBBrd7fr4/X1KG5jkqdhYcinHjsGckhPB2lHROD5/n543kTYM9lkSFZoZrdziez6euy3bW2ectvTwfz5vEWZYWwMefpgTqU8cADtyFYrIhLt7SB1mw0edHc3Hnevju/uRoSCPd7djbWSTvkUBJwvk0iNicG5u6/T4CD65t95B8bWu+9Cxvy11yBeptPxouz2dt+SqywiIm0tFEXcL+m2ZTLBOOnvD3S1OJRKJe3evZu0Wi01NDTQsWPHpn4wbygqQpWlFD09CMvMURInkj3yOYnx8XF6//33yWq10qJFi6hkShJJMmTMHDZt4kM41Go+VKWggBf9hoWBIPbvh7Pk7t1ptSDvZcvgkd91F0S4LBYemg8Px/uGh7l06rRbnSRYtgyhajZH3GLBZz3+ePBqnUwmRHCzsngalmmcfPYZl8MdGsJ6bdyIv1kxIavBKijgevREXEZcrcbvLHqgUCDM/sYbfHCY1YpQ+NAQvHfWEmgw4DX19a7qeRoNyNxbdCA6GlHnw4dxrxUKHGPJEhhrTifSJCdP8kLI4mLoBLiPGfcHOp2OHnroIXr77bepvLyc0tPTKXs6iX4p1q+HxdLSwrVmw8OnLkY/Q5CJfA7is88+o+7uboqOjqadO3fKeXEZcw5OJ7yr7m54e/PnY2JjXR1CxQkJIGzWlsQQGgpSYpKu0q+2xQLvkQj7Z0ICio9NJnh9XV14/cgIit26u+FRBjNvrdVi2Mv58+hxT0lByDuY84iYeiczQPR65MbPnEGaQavFGgoCdE4WLgT5VlfjPNiaXbuG9yUmIkzf3o61tVr5dTBkZKDw7MoVkH1WFnLjP/sZ3s+OGRqKCElzM5xQFrUeH+f3xhu2bMExz5+HEbFjB85boUDOvrwc584Ml4sX8b3ZsmVqa5iTk0Pr1q2jo0eP0gcffEAvvfQS6aarTzs+joVfvx5hEbMZhR5FRdPv1bvFkIl8juHq1at04cIFUqlU9Oijj1LIVCSrZMi4hbDZMMe7vh4bsyjCK3v+eVdZzvp6EIe0mHhkBASdnIwQcWoqjjEwALJi7y8qgjRrYSE8Oa0We6nRiP01LAzH2bkz+NcXEYEWuenohkwEnQ5kJpVWXbIERG4y4fri42FEmM0Iey9dCk6RGj7JySiyfvBB1Bs4nVhDrRbvLS9HMTeDVKudweFw9Yr1eqxrYyMPlRuNqE1YsMD3NQkCChDz8jyfO3kSx5TWj6Wmophu06apK9OVlZVRa2srNTY20p49e+jpp5+eutNjMCBkMTzMH7vnnsmr3OcIZCKfQzCbzbRv3z4iItq8ebMs+iJjTqKyEiQtnV/d3Q0yeeYZ/tjatfAiDQaEqUdGEHJ96il48JGR8NYcDpDSU0/xfHhxMdqpWLFXQwM8uMceQ8g9PR1kNVvypNNBdDSf65GSAoLr78f1abUgcXZdoghu6ery9IjHxxG5aGxEq5pWC2+YhbevXsV6T5TbX74cIXFpxIFNs2NFhrm58LCnWmtrsXhKtiqVOP/p6MQrFAp66KGH6Fe/+hU1NDTQuXPnaOVUpo05nVzMgPXnORxo7s/ODm445hZBJvI5AlEU6ZNPPqHR0VHKzs6W8+Iy5izOn/dUbYuPR1hdqvIVH4+K8vJykE1sLMROWCHxzp2YljY+7hm51GiInnsORN7YCFXMwkLvIlu3I3btwrWcPo3rz83MUY+UAAAgAElEQVTFv6dOuRLbyAjIPiUFxJqWBvK+dAnGTUICqs0FAVGNkREu+a1QeJ/3LkVpKdGNG6hNUKnAX/HxiK5otfh7ukHBxYtxXVJtFqMR3nugdQdOJwy806cRGSoujqDNm++jPXv+RAcOHKCcnByKjo4O7KA9Peihk/bnKZWwPi5f9p/Ih4ZgcYWF4WJn0MqUiXyOoKqqiq5du0YhISH0wAMPyHlxGXMW0kmOUgiC596VmAgv2hdCQnwThUqFcO5EId3bFRoNjJhNm0BOajWiHKdOgVMYqcbGwhPfsQNV7Y2NyC+PjWFtS0sRuj57Fu1m0dF47sgRFO5NlNcmAud87Ws4bk8P3j9/Pg+3B6PAb+1aGHktLVyGNjyc6N57Az/WZ5+h6yE2Fuf2+edE6ekLacGCxXT1ajV99NFH9Pzzz/tuSfMGX7KtguA55ccXjhwhOnQIv4sirKFnn3XV9r2FkIl8DmBoaIg+++wzIiLavn076f9a3A4Zf5W46y60kWm1nLg7O+F5TaUK+XbH4CC82shIOG+BeLCsPuDSJfy7axciHiEhIFWWey4qwvoeOoSitvnzwRVKJcLp4eHw2GNjwT12Ozxzf4hYpXLNb4+OIn1y/ToMgRUrEGqfKiIjiV5+GTURbW0478WLA68fGxiAMZOVxb93Wi0K80pKtlN7ezO1tbVRRUVFYAqYCQkoXBga4iEfpxPhjcWLJ39/QwOzKPiCd3ejzUBacXgLIRP5LEMURfr444/JarVSQUEBFUl7PmTImINYuhSh2Koq3gqVmgo56jsJ4+Ooj/rDH0CcajXC/9/7nus0t4nAZqITISVhMoGo0tJ4m9ayZZwfkpKQxmUa5nY7wuesZkClwnGklej+YmQE3v4f/gCnkonSnD6NNIe3QjZ/ERqK61i2bOrHYApy7s52SAiR0RhGDzzwAL399tt05MgRys3NpQR/Z4Erlegv/N3vYC2wL3VpqX838uJFWCVSqykxET2M/f2wyG4xZCKfZZw9e5aamppIq9XS/fffL4fUZcx5qFToSy4r4xXN6em3Z+GZw4G0piiCJAMJJe/dC132pCSQic2GArNf/pLon/5p8uIwpxOV+TodH2MaG8tbv6SjWnt7ETKPjMS5siIxpRJe6cAAiJZxhtEY2KQ4g4HoP/8TXnNLC3hpdBTRF6sVbXA/+IH3e8zkdaOi/JtDzmbQ19Rg3ZYt42loux0G4oULuLaVK3m+PyLCe0rHZmMpgfm0cuVKOn26kn796w9p164XKTNT5V9dRXo60d/8DUIro6P429+JLzabbzEDJqt3iyET+Syit7eXDh48SERE999/P3SDZci4TTDHJjlOiO5ukGFEBDc6OjqI/vhHhMYFAc898YR3AjSZuMpcRATyvAcO4HcWSmca7U1N8LQLCyc+p8FBHNN95GdUFNr27r4bXvKf/4z8uSDA0NDpQPYs9K7Xg2wFAbwxOIjzW7/e//X5+GP+e0ICPGijEU5lTg7+NZlcK+DtdnQqVFbiswUB4jXr1vmOBjidGHxTXY3rcDjw/vvuw/W+9x7qy2Jj8dq334ZjvHMnDKb58xHJZh0Lvb0wZJhQTWHhZvr1rxtocNBAdXXllJ19j/9T3sLDXVVw/MXixThpdkOI+JfFXe71FkEm8lmCKIq0b98+stvttGTJEiooKJjtU5Ih47aB3Q4naLIAlsMBkjp/nquKpaUhovDmmyBGRtwmEx77m7/h3jQjq7NnuTe6Zg08RYfD00PVaOCd+lMjpdHA+WttxXnExXFVvMhIvGbPHjiJ6em4VpsNeeZ162CIiCLRK6/AEz52DJ51ZiYINSXF92e3tCDf3toKcq6rQ8okLAznz4Rh2tq4CI177v/oUYTd2SyS8XEUo0VH++bDxkZ44kxJjoi/b948PJedzZ9jlf2rViG3/thjSEdfuIBrz8oiuv9+kLnTSfTnP2uosHAX1dS8QWbzSdJqF9GnnyZSZqarXGxQsXAhhACqqnBT7XYs1vPPz1iYSibyWUJVVRW1tLSQVqulrVu3zvbpyJBxW6ClBZt+ezuIZsMGopIS34R+4QI8vsxMvqe2tyMkPjLi6n3rdEhp3rjB88HHjqHPev587M0OB/6eNw9E2dyMx1hk1WSCE+ZPWPvCBV4trtOBxFesQAi9pATHunIFhge7Pub1j45iiIkU/lb3t7YS/eY3MBYSEnDNly6BKLOyQN6hoTx839YGIpWGzR0OVMtLe/nValz7iRN4no1jXbQIletdXfjc+nocOz0d72FSvVeueBpnCgX+7unB+YWHQwBn+3ac8+nTmH1eUIDr7+8nyspKp5GREmpqOkNXr35CWVkvUE2NcOuI3G7HjUtJQWhk3jzMc2XW2AxAJvJZwOjoKB04cICIiLZu3Uph/iSWZMi4w9HZSfTb3/Lw+NgYcszj475Dp2fPglykjlFyMjx0bzVILB9stYLwz55F+qChgc/bTkhAm9jjjyOM3twMgrVYQPYvvDD5gJWODhgk69YhKtvdDcOivJzoJz8Bofoq7tJopjdV7PBheLDs+uPiED4/dYpo925EG6qq8PmFhfh72zbXYzgcuN6REUQJWAV6SAje29KCdYqKgsHy5psg45ER5PObmkC8mzfjepg6oLdOMFH0lOE9cwaRkoQEVNZfuwaDjb0/P38jdXXV0sBAO4WHXyCHY/nUF4wd1Jt3XVeHfABr2NfpoIo0gyROJBP5rODQoUM0OjpKWVlZtNif9gYZMu5gtLcjnLp/Pzy8lStBlEx34/BhFGV5G7HpLfxNhH3Wboe3SQTC0WhAQkuWgDg6O7E/Dw2B7K5e5aF4Njnsn/8Z53btGoyLHTs853t7w9Wr+LevD2TE2tYGBnhIPDoaoWWz2bVVa3AQofOpor2dtzeLIgib5cTPncO1LlyIn+3bvad5m5txzQMD8JKjo+GUGgyIJBQV8fshijBWkpOxdiYTjIDaWqxVVBTy36tXw8AyGvGZoojjJSbiPjc3Y91YVCQnh39GYiIMiq4utl4htGjRNjp37n2qq/uCXn21gIgCrEGyWPBBlZX4shQVwfJgVtrgIEr8o6OxCE4nwh0/+xnR3/3d7eeRC4KwjYh+TkRKIvqtKIr/4vb8V4jofxJRx82HfiGK4m9vPvccEf3tzcf/SRTFN4NxTnMVbW1tdP78eVIqlbRjxw65Sl3GbY3hYWy2Wu3UWp4mQ3c3wrGhoSDa8HCQjd2OjVyjwQY+NuadyJcvx7xuKRH29IB0q6vhhbJwrl4PAsnLg2ccGYlrMhpxfL0evdVhYTguEfKuL7wQ+HV1dKAnWlrZXlCAdWSV2QoFwshvvgnOCAmBR5uVNbWaLIbkZC7+cvUqCJkI16pWw8ONiEAI/Pp11HLdey/npb4+ot//Hq1xFy6AWLu7MeFs5UqQrvReNDfj3+FhXIdGw4sHDxwg+s53ULMQHk701a8SffQRPHoiREAeeABqqceOYQ3MZnjk7uPG9Xr8mEw4R6KFJAg5lJzcQNevH6TCwl3+LZAo4sL//d+5QEJSEhL47e0oSggJwQI5HDjx4WGclNmMC/tv/w1fjCVLpn6jAsC0iVwQBCUR/ZKINhNROxFVCoKwVxTFWreXvieK4qtu740mor8nohVEJBLR+ZvvHZjuec1FOJ1O+uSTT4iIaPXq1RQ7QxWNMmRMF4ODPNyakYG856lTcFiIeOHR448Hd1DUqVPYsGNjQTxsvOi1a/BibTbsoyz0OjgIElAo4O2tXAmyYa2+Gg02ezZiNTcXr2f7L/svOToK4yEpCUTe14fnenvxedMZqGKzgRNUKl7ozKRHly93LcqaPx9EV1WFc87NxXlPR3hn40YYR2NjiAxrtTAQSkqQh/7wQ/BPbi5eX1ODNXj5ZaxrTQ0eT07GWrKZ8OPjRI88Ah0Uad0AE60xmWAkaLV4X18fvP8tW7iTGxcHDZXhYd5J0NlJdPw4jC+m0V5bi/VKSeG5e7MZXn1pKXjYYhHoySd30Ecf/Yqqqi7R0qVLKNMfudX9+/FTU4MTO3MGi7F4Mb4s9fX43WbjN+/MGd4HR4QQ+/vvY5Hi46d+s/xEMDzyEiK6IYpiIxGRIAjvEtEDRORO5N6wlYgOiqLYf/O9B4loGxG9E4TzmnM4c+YMGQwGioqKorKystk+HRky/EJHB3LTdjs2zfPnsdmPjWF/Y73Xra3orX7yyeB9dns79wRzckAaLC9rNOL3Rx7BBn/2LD6fpTSVSpCvwYDfDQaE4DdvhpCL1Yr3dHeDWGw2EHVBAbzT9nbsxxkZMArMZoTTv/Wt6Y1O7eiAQ1dcDIOEeeB2O/hB2ssuiiDt0lLPkbBTRWYmnMXXX4fxotOhmC05GWsxNobzYymJ1FR41c3NfB2Yx63VYr2IcG8iI0Gm5eU4nkYDLlSrXcmdafIvWIDiQnd+lUalmWHG3qtWw1M/fRrnm5EBo0ChgOEWEYEKfCCaenvX0pEjR+jTTz+lb3zjG6ScaIC9wYAqvthYXFxkJA544wY+SKXCl4QIlqvTiQo7sxkkbreD3BMS8LrqakxRu8UIBpGnEFGb5O92IrrLy+seFgShjIjqieh7oii2+Xiv16YJQRC+TkRfJyJKl4rb3yYYGhqiI0eOEBFkWNXe4oAyZMxB7N2LjZ3JdMbGotCI6V2Pj4Ocenqw35WWBiZG4g2iiP0xJgYOEBtjWlYGR6mjA8898gjIoLcXRWpJSdxbvXQJEtiPPQaiYDPUa2sRUu7thTEQFgZCU6nwc/QoQtfNzSjKyszk/fJf+9r0558zrfqCAniUAwPc05RqkDQ1oXVOSlL33AMDg1XHT1WIJycHam2i6EqiY2PgIfftSRD4hM/cXFSmS+fJ22w4j8REnFNEBELho6NYy5QUGIOMA0NC0OceHT25gRIS4ikEk5+P78f4OAyIvDx49t4KGEtLS+ny5ctkNBrp1KlTvuVbu7uh7nbqFLzo0VGEf9hFDg7iS8T+I6Sk4Au5dy8PIYgiwhmhobipNtvEFxckBIPIvWXF3PV39hHRO6IoWgVB+AYRvUlEG/18Lx4Uxd8Q0W+IiFasWOH1NXMZBw8eJJvNRgsWLKBcFrOSIWOOY3QUpOluO0MWE/vUiRMgwtBQbNS//CXCsNIxp4GgowMiKMzjbmjA5zDhlIQEpCmlAwLPnwfxdXZi701Px3GY6lliIogmIQE59sFBkFZ4OIhfowFhbtzIJbc3buRDXVJT8XnuU9+mgpQUOHomE7zhyEhuDLEWsp4eeMx6Pa7F4YCB8dFH4BFGbHl5iIBMJdSemclb7hgBiiLvaWcQRfywx3JyUM1eXc2LBi0WTKhjYe61a9FJ4HSCz1iVe3s7Hhsdxb3q759cxz03F4aFtOhvaAhr9f3v43wnMmZUKhXt2LGD3nrrLSovL6eioiLSMSk9hu5uol/9Cl8WjQbhmsFBnHhSEi6ytxchE6ls69at+PsnP8FiskV1OnHB+fmT3YagIBhE3k5EUm2iVCLqlL5AFMU+yZ//QUT/Knnverf3Hg3COc0pdHR0UE1NDalUKtrm3schQ8YcBtsk7XbXkG98PHqgmeJXTAw255QUbPgffUT03e8G7i2OjCDsrVaDwBixtLXxPuWnn3adZdHVhXRkWxs+u6cH5zY66im5qlZjfy4sBDHa7SBRIl58HB4eHM/bF1QqzF5/6y1e1CUIEDZhHjkTsGF8o1SCvK5f5w4fEXLcZ86AOL3BakXR9YULuPaSErxfqQRfPf880bvv4jwEAffxwQdhVDDi7unBe9i5KZWIcixZgt7v8HD87t6nLQiuefJvfIPoX/8VRX6hofhJTkb31iuv+G7Zi4zEILF332VFbHjtU0/5b8BkZ2fTwoULqba2lo4cOEAPZGUhNKPVotz+1CksUEEBrA1BQB5hYADetkIB+bmNG13DFYIAS+PHP8ZM86EhWBwWCxZ7hmaZB4PIK4koVxCELEJV+uNE5JIlEwQhSRTFrpt/7iSim80X9DkR/bMgCGzW2xYi+q9BOKc5A1EUv+wZX7VqlTzZTMZtBY0GeeWTJ3kY127HJrxqFTZlliZUqfBavd5T0tPphNNjs3Ftcm+4dg2eMqsPYvskIx1v++Jf/oLXd3biuOHhIGubDecqDbf29CA33dQEMZlLl0AU4eEwIiwWOFi3Wi05JgZ53PJyXNuWLVg7hr4+14p2pgmv1YKcGZEnJICovRG5wwGJ0xs3sD42G9Gf/oR78+CD/P3f/jaiH04nXme345jnzoGAd+0C10mhUqHgcdEi/685OhrRkm3bwIVsOltbGz5v82bf783OJvrhD7EGCgW+QxOlur1h06ZNdO3KFbr01lu0KjOTElJSsCiVlSDrggKc2OrVeMxsxvM7dsB6nEiPeNEiWK61tfgC5+VxybsZwLSJXBRFuyAIrxJIWUlEr4uieEUQhH8konOiKO4lom8LgrCTiOxE1E9EX7n53n5BEH5CMAaIiP6RFb79taC+vp5aWlooPDw8sNF6MmTMEWzaBJKrquJKW/ffj/3u5z9HiDUxEd5VWBgIRCrp2deHdluDgedfH37Yuxa52ex7gx4b83zM4eB1SKKIc2RDRRwO5JW7u3EuFgs8+ocfBsERgRBMJjheCgWIcudO32shigj1MxWyxYsDrwew2TCgpLubR2337cMas4BdTg7y+NJx1qxYTGpkSPPU7mhsxNpIUxwREeCoNWu4xy0IroXVrLiutDSw65oMw8O4B+5pmnnzcK6TgUVppLDbcd/84cvo6GhamZBAZ/r76WBsLD3NFtdqJfriC3yJ4+Nhid5zD6w+qxXj7PyxGmJjkTOfBQSlj1wUxf1EtN/tsb+T/P5fyYenLYri60T0ejDOY67B6XR+ORRl3bp1FBqsslMZMmYQISHo8928GUQbE8O9xQcfROowNRUE4HQiMrliBUjd6QSJDw9zwrNYEIX8znc8O3PS0xHqlhIU0y335hApFDgXqxWEFR+P6MDoKEjy5ZdBugYDwv4LF8Kbfe45FOw5ndivtVqkO0tLQSzj49770j/5BNEJpu198iTIN5B2tGvX4FlKowtaLVqs7r4bPFJcjJB5ays8WVblHRPD0wWiiHO/7z7vn9PZ6XkNjPSMRoTtT58GsSsUiAiUlHi/7mAgPJwX9Uk/g/XGB4KrV6GMx+5daSk4dLLpdWV6PV0KD6cbRiM1Go2UHReHL3haGhYsNBQLY7Hgy757d+Cu/yxAVna7hbh48SL19vZSdHQ0rXCPTcmQcZshKsrVQySC5/jQQ2i7dThAbkxAhAiEZTC4eq2soLemxlOhLCMDJHbpEgjV6UTacdMmz88mAtmXlYGUMzKwqWs0IMBNm/C3tCiOQa9HkdhDD/FzEkW0ox05AsMjNRXXwQi3owOpVKluu90OUZPiYhyTzSWfCC0tnuM+lUocs68PxwkPh5b62bMgrfh4EPbx4zyvLoqI6Hq7PiKsl7fhLUzy9O23EV1ISMA679uHYz/xRPCFfYjAl2vXwvllht/QEIywVav8O8bICGoL3n0X56jTwTg7eBC8y6IpfX1IDbAhMkuXIoWiTUigNcnJdKivjw5evUpfj41FxbVejwU+fRqLEBkJEr9N9m2ZyG8RbDbbl+1m99xzz8S9izJk3MYoKUGLUX8/CEhatDQ+7j3sqVJ5D5UrFNg/Fy5EmFylgkjKRI0eq1fDAz9xgh9jxw6Q62SQBskqKkBmSUnwggcG0DL1yitIG7B+Zun1MA/wwAE8PziIkPW99/ouWI6L49LcDKII0pX2T2u1yONv2MAfW7QIn8MKDFNTvc/oJkKaVq9HCD8+Hq/r6oLBY7d7ht2zsmBcdXZOPDltOtiwAUbL8eNIMcTHo6fd39HfH30EY4ppxY+P43uybh2Mng0bYBz89re43vBwtC+eOkX00ktE84qLadXhw1Q5MEBdQ0NU3dZGRQoFvmB33w2LwmaDNTZD+e1gQCbyW4SKigoym82UkpJCC9mwXBky/krBKpDdkZiIjZuFhomwwY6N+SY6lQqGgTcZ0sFBKHoZjSAeFirfuhXe3vAwyCvQLJbdjrGezFMkgkdrsyF8/sgj8KJFEeQxPo7PUChAlD09IFmmJf7GG1Ao86a7XliIz2Ka4g4HvP2FCydvb1Mq+TEvXkTxWl8fvM6tWz0jHy+8gHRAfT3OtbgYRkZ1tWfEmM0U7+u7dUSuVIJs167F2oaF+e/9Dw4iOqHR8PurVvOCuZgYrP3+/XieFTlGRWF9jx0j2rkzjtRf+Qpt/OUv6eOLF+nQmTO08OmnSbV7N17sbV7rbQCZyG8BzGYzVVRUEBHRli1bZD11GXcsQkMRvn7vPWzizBNftsy/4SJSsOlnbNzz+fMwFF54AR4aax2bCkZHQSzu7UwRESBqIhgOra3w/NRqnENGBrzcjRv5Z+t0OMejR71fY0QE2ts+/RShbaUSzuCmTf6fb2Uleu0TE3EO/f2QXd2+nQvIFBaC4J97DoaUzYa8+//5PzAiDAZEH6SpAFHkLW+3Ekx8JxBYLLxFrrOTr7dKhfvH5F9bWjyL4mJiYATs3ElEeXlU9NOf0qmf/YwM/f10Zv58KnVvU2CN/QoFLNRAT3aGMbfP7jZFRUUF2Ww2ys/Pp4zpSlzJkHGbo6gIhFNdDRIvKADBuUcunU4QW00Nnisqcg397tkDomVFb3FxINbTp6evgqnV4mdszDV/PTQEo4MIJMiEXMbHkZO9fBlE6k5+UgPAGxISMCDEYsHfvnLrfX3oAWfFegUFCEd/8QXvEiCC93nlCtG//Rsf6HLyJLz0xYuxTqwyPjUV53fuHAyj9HQQnU6H489V4czYWJC3QoHrHhzE/WAys+vW4d/QUNwfqVFmteJ9n3+O6ElWlppWb32IPvrobTp58iStXLmSNOwNDQ1Iwo+O4u/ISLSf3bKB5tOHTORBxsjICFVWoptu/fr1s3syMmTMEcTHT062n34K8omIAKmfPo1K+Y0bfSvMxcQER85aqUT1+XvvcWGY/n54gKtXw5utqED4vKgI5KFQgIivX+cqbQyDg5NHHEQRJH34MI6j1eIcmE54WxuIloXeb9xAFGDNGi7SwjA0BMNBp+OGjt2O98fHg8guXoTxwyTB1Wqcd0cH6gGYYt5cTQ2rVOhp/8MfkNLu6ICBkpxM9M1votVQEFDBfuAADCxWJd/UhPU2m3Fv6+qIdLociolJpb6+djp//jzdfffdeMHbb4O8WZ5jaAgj6H74w+lNq7mFkIk8yDh9+jSNj49TXl4eJU2mPShDxl85RBEEMz4OomDpRzZr2mIB8fT1eVaEOxzIJS9ZAnL3pjA3Pu69mn0qWLoUnl55Oc6noAB64LGxIDyHg3vN7DOVSpxzXx/OLSICJG614r0TobISUYbUVJDt2BgMCTZM5JNPcD5tbVjDtDRwSlsbiCkxkZN2fz8+MyaGH99kQn92ZiYvQlSpEFkYG0NKgAjcFBmJ8zh9GkVycxULF2JozcWLMGZCQ3F92dk8115Whu/VqVP4W6nEOjIjhgj3r61NoOjoMiL645deuer6dVht0hF+ej3i9U1NE0uusr7JWSB7mciDiLGxMTp79iwREa31pZkoQ8YdgoEBoj/+EflMhQIk8tBDIKR33wUhMRnPrCz8LvUG2Zzwzk7ke0tKsDmnpXFS7+tDhXqwUFDAp3lJERGB/Vyq982usawMbXhHj8I4yc4GiU9UiS2K8MSlKndhYSDi8nKsR3s7iLq5mY87jYgAQeflIawfFobHzGZEMaTV/Z2d+JzmZhgCbW1ct72hgc8FYa3U9fXBHUFLBGPh2DF8dlIS1opp5k8V8+Yh8nDsGNbk8mU8fu+9iFaoVKgVKCxECqK2FkZTURGuk6XDY2OJBgdzKTExkbq7u+nixYu0ko3O8wam5euO4WE0tbMTWbQIJzCDKp4ykQcRZ8+eJavVStnZ2ZQ23W+rDBm3MUQRoi99fa5CMO++C29oZIQ/brViU/ZGIk4nJ7rNm/G+y5c54W/bBi/tVkOhgJrdW2/hHJgMbEQEhFR0OtdQOmuHu3KFjwmV5vsdDuz/7tO6wsMhsKNSwfsfGcHjzNscHwcRZWeDlMPD4ZkykpLW1Q4NwVOPjMSxBAEhZY0Gxzeb+ZROQcDnBjOs3tFB9Otf8xnwbPLc17429YE6FRWoSj9+HMdlY8KdTjw+fz6Mn7o6zEC5eBHX1tqK9WhuhpHFNF+iowUqLS2jP/3pT3TixAla9uijpGS9gKysf3wcB/G2pzsc+FKwIga2yAYD4v0zNOVSJvIgwWq10unTp4mI5FnjMu54GAzYyN3boWw2VJtLe6NDQrD5trXxyWNEMAKUSmzeb76JzbesDPlwaZWyL4gizsFiQVhf2qM9FRQUIId86hTOrbgYUQL3QjeLBRKsXV0g6t5eGB8PP8z1RVQqhLIHBlxTAwYDiPX8eXjdly5hDdiYazYW1GSCESNVfW5thaHU2oprDwmBx97by8eMOhz4OzmZ653bbLwlUKr3Pl0cOoR7zlLNoaG43s8/xwCVQHHtGlIRzKuOikK0W62GE6xUol4hNhYV/QYD1j8iAuvd1ATjqa4O966/H1XsBQULKC4ujoxGI1UZDLRswwaESzQaLIzdjrCPNw+7pQVfMqlMX3IyLIbGxttq+pkMIjp37hyNjY1Renq6XKku444HIw5vsNs9H9NqUVQ2PMyJKDISx2ltBelZrRAE2bx58lYtkwk1Sx0d3EvdvDkwKVVvSE1FT/lEuHzZU4JVp4PHWFTEU6j33otiNJsN19rWBuJetAgjrpmOeGwsSCwsDNEHux0kxoriGNLTiX7wA4TRBQHeL5OnZT3vsbG8+psIazs+DsJbujS4UuFNTZ598VFR4D6nM3Dv/8QJLgJDhGvUaiEIo9dzx7mnBwaPycQjHomJiEAMDoLsU1JA4nx49v0AACAASURBVBgbK9DatWvpww8/pBMnTtCSV18lRX4+Fl2hwKL7ypOwOeTuEAScwAxBJvIgYHx8/Mu+8bKyMrlvXMYdj8REeEruQjCCgE10dNS153t4GLrtBQV8uEpNDfLFCQl4TVgYPPxjx1CZ7C5zKsWHH2JDZza13Y40ZkoKwq+3EjdueHrpISEgmr4+Pn87MxMe/smTyGcPDsKYYRFcpxOO3SuvwJO+coW375WUeI9GKJVczKXz5jDp4mK8T6GAwdDQgL8TE7kMrtkMIg9mjjw+HseVOrIjIyDXqYTwh4fxXWKpAoMBRsvoKKI2NhtqMJihxNrQWFohPh7Xy+aYS0WDCgsL6ejRo9Tf3081NTVUVFTkXx9eTAwf2C7d96UD3GcAMpEHARcuXKCRkRFKSUmhHOnQeRky7hCwKmE2R7ukBDnlP/8Z5MLyvcuWwSt95x2ENtnjixYhlMxGVBKhhcidWFQq7JEmk28iZ3O7pfuwSgUCOH/+1hN5VBTCt1I4nfhxF6xJToaHbzTiR5qGZfPIb9wgevzxwMPe+fn4PIsF5+R0wlhwOpGjLitDmF0QQHAGg2tqeLrYsAEKdyoV79Hv7oaW+1SwcCG88rQ05MXfew+Ph4aCvAsLMdL2Rz+CkdTTw4fOiCIiOpGRkFR3V/5TKBS0du1a2rNnDx0/fpwWL17sn0OWkoIPvnwZloIgYCFnuCFfJvJpQhRFOnPmDBERrVmzRvbGZdxxcDoRxm5shPcsiugJLyxEq1BNDbym/HyQqFKJyWfV1fDYcnPx404gKSkgZGkOmYVPJ1Ifk4ZepVCpPDXOA8HYGI45kfyryYT9fGgIrw8Ph0fa28sHq3iDIHjXTBfFqRegRUZiMMxf/sL73vPyYDhlZ3MRHPY5AwPBI3KLBdefmgqjJjwchPrII67974Hg7rvxXWKa9vHxMASLi2GYhIfjuZYWTOsbH8c5tLbi/QsXEj37rKf0r8mEDoGwsCIKDz9CRqORGhsb/XPKBAEflpUFyT9RhAW7cuWMNuTLRD5N3Lhxg/r7+0mv11P+DBU2yJAxl9DUxPuVGTIzEQpev957Pjs21rXgzRtWrEBfc3c3opQWC37fsmXisHp0NCKe0sI5IhDVli0BXJjkffv2cS974UJ4ddJjO50gzIoKRBrOnOG5b6USId+J5pzHxMA7Nxp5RJZVtk+V+IhQYDc6CqJSKMAzpaWeRo7RCCMrGC3Qw8Mo9jMaYfTo9UgtPP88T5NMBTodiuSqqlAwl54OvnSP2ogiPvPll7HuJhNeExfnWUR++jT69WFEKcloXEGRkYfp7Nmz/kdXVSpYGXffPfWLmyZkIp8mWN/4ypUrSTFXJZFkyLiFMBo9nQ/WEz7VARxOJ47xla8gnHr1KkhRWvntC2yC2htvgMyZJ75wIaIEgWB8nOj11+HFsrD39euoon/lFS5Oc+4ccvdJSSCa7GwQSE4Ofu/rc60XcAdz7H73Oz6mlAiGkLQ33OmEMWOzufag+wIjv5YWRD9iY7GOv/0tHgsP57K027cHtja+cPKka9shEaLNn38Oj3g6kI6lbWvjSm1MZU+l4hFtQXAVzXFHZyeKClNSOMGHhS2nY8fKKSKingYGBijKm9pQdzca1K9d49qwM+yBu0Mm8mmgr6+Prl+/TiqVipYxQWYZMu4wsIIpd0x1AEdtLULzjIRLS4n+9m8Dm1uRnk70ve8hKjA8jAhBTk7gYeOGBj5djIF1FzU383z7yZMI9bLwdEgIn7rFWp0aGrgOujfExRF997s47tgYPic2lj/f1wd5UlYMqFbDsJnMOJFOTGN4+WWsTVsbznvx4um35zFUVXnWecXFQXDGXZkvUAwNwdhpa8M6HTyI8162DIbDE0/4Pzintpb36zPEx2tJpyskk6mKKisraYt7CIdNp1EokDewWFBZOTICLeFZguxCTgNMU33x4sUUPtWxSzJk3ObIyUHItLMTJOZwYKNNSwu83qe1Ffl25lnFxaEf+ejRwM9Lp0O0c8sW5Iankvs1m70/Lgiuz42NeYalmc43K2j2NTdcCrUaHnhRkSuJO50gcZMJhJWeDkPhnXdQ1BUoQkNRj7VmDTzcYJE4O7bVCse1tRXGDSPw6Tqt+/cjAtTWxuV5+/u5jnwgEReHw/v5JCffdVMH/wLZbDbXJ8+dw8XEx+PN4eG4GeXlfALOLED2yKcIm81GFy9eJCKiu4KpoiBDxm0GtRr5z88/56pry5ejbzvQjbuiwrUIS62GQXDiBKqsZ1rGOj7es7uI/R0fz19XVIRap9hYvM5uR246ORmEQTR1NTMi9KUbDJ4CO0ql/0NjTCZUwI+O4t+GBn6c++5D5CAYWLSI6J//GfeKGTChoZjPPh0it9kQRSBCzn9wEMdNTgapv/8+6jH8JfOCAhiI0gK/kRGi+PhkiotLpa6udqqurqbl0jBKRwe3esxmWCojI7C0enpmbXScTORTRFVVFVmtVkpPT6dEX0kYGTLuEOh0qEh+8EGunx4IGFH29XmGRtVqEKPF4krkooj9M1jtUt6QlgZiqK7mHnJvL3qupRohZWVcmTMzE+FllQoh7c5OFDJLB5oEivFx7ySoUvnnCNbVQffebkeIu6MDnvjChYgmvPsuUiTB0LJqa8PasOlxDgfu1XSuX4qBARxbq+VRj9BQfE8OHPCfyNPTkd4uL8dxRBHHeOopIovlLvrgg3Y6c+YMLZs/n4Rr1xDXFwT8Oz4Oq5MIN6a/H5bEyy/7H9sPImQinwJEUfyyyE32xmXI4Agk/+l0YpjFkSPIY+flIVR67Zqr2MnICKqQWXWy04me9fJyPJeTA7nSiYaUTBWsCC03Fz3oRChAc68k1+lQ/FZTA2/xgQdQQBYaCk9cGiafChITQTbuAjtjY5OrgFqt6LmOisL9uXQJhF1XhzWbNw/rffbs9Il8ZASe/ooVcFBtNpy7KMK4mc52qdEg8vGXv+C4rP5idBTn39cHg2t42L9UgSDge1NUhHy7RoPvoE5H5HAspM8//5x6rl+nln/4B8rUarF4TLCd9Rayx+66C2R+7lxw5fH8hEzkU0BzczMZjUbS6XRU4G1UkgwZMiZFeTk2ZUYm7e2IVqrV8OqiorBfjowQPf0090gPH0bRcHIyvLzubtQffetbwfP6pFCr4b2yamlfCAtD8fLKlcE/h9BQFLa9+y4IXaUCgS1fPvnc8/Z2EF94ONZSFHEMhQJrN28ejt/fH5xzbWmB0cPC6i0tCLcHYxjYtm34bhw7hly5Wo3vyPg4H2Tzy18ijO8+kMYXkpM9jUClUkkrli+no198QWdjYiiTafsmJ+MD6+pwE5RKWC3p6VjcmhqZyG8XXLp0iYiIli5dSspbGdeTIeOvFFYr8pPp6bxqOC4OG3JhITyqGzewb65ezVOPY2PYxNPTufcfG4tQcWUlNvqpQhRBDk4nr2UK9P3V1ZjMNTSEHOy6dRMbF1YrrtkfadTFi1FUWF3NPfGcnMnPU9ozzqIEVqvr2NiBgeAYIEYjDAKlEgYCETzkkyeJ/uVfpn98nQ6V/UlJRK+9hrQFG/+q16O4cWQERuKDD/p/3MFBcPDAACIo+flEy7KyqHx0lOpCQmjMZqMwltdJTcUH33uva17HbHZVL5pByEQeIGw2G129epWIiIqDVR0iQ8YdhuFhEKa7QIdWi011926irVs932c2gzDdQ/gREfAup4qeHni7BgP+jooieuwxEIbT6V+R3alTmM4VFwfCuXwZ/e+vvurpjVqtKA48fx55azbEIzV14s+Ij/evsE2KtDR4qyYTzmvJEhDr2BjWu6UFxtBk/fn+oKoKoWrWtse88ogILr07XSiVUKxbvBhDYlQqrPmCBTxNcOWKJ5HbbCgaVKsR7mdGTFsbtALsdtznigqQ+XMPRlP2vHnU4HDQlc5OWsF6EAUBfYft7Vjc0VGUzTc0oHgiMhIkP9FoviBDJvIAcfXqVbLZbJSenk7R/sZuZMiQ4QKdDhuyzeZKksPDE1dPs/exYRgMJhN6iSdDXx9IOzwce7BCgWP97nfYyFmOuLeX6Mc/5p7/woXYm6Oi8H6TCV4gc8BsNvQ0p6Xx60lOxl5fWempbvfRR/CsU1NxPX19RP/3/8LbjI+HAVBTg2MtWTJ5+HwiqNVITbz1FjxOIpBeairCz3l5WLtg1Gix6MKGDVhDpm9uMnkfEjYdFBYi4hEZ6Sq0wz5Titpa6P6zka0JCTAGYmLQBh4a6upMNzURXbiho+KVK6nh0CG61N4OIrfb8SX96ldx0PPnkRd3OtHLl5UFa6a/n+jFF4N/0T4gE3mAqKqqIiLZG5chYzrQaOBZfvIJNtXQUGz8avXEId6QEJDivn3wwsLCuBToRB6l04npZydPcqnS5GSiZ54BMQ8NcRIXRezRra2oQE9NhZpbWxs8ubo6foxVqzCq2mTiHp0UkZGuSm1E2OOrq2EkCALIvroa19HZifNyOkEsDgeK0O69d3ojWOfNQ0G10YjzTE+fmljPZCgsBK/FxHA5VpMJEQlpu95UMTQEA4eJ9Nx9NyrVMzJwTwwG8OjatahJy8zE9+qddxB1YNK+RiP68p95Br+7d43FxCCi8vzLL5OmspLam5qoLzaWYsLDESoqLMQPy5nn53PLMi2NzymfLMQSJMhEHgCGhoaoqamJVCoVLVq0aLZPR4aM2xpr1sB7+9OfsDlrtSB3NvTEF0pLQZDHjsHDLCyEBzhRMVVtLXLXmZk8pMokOt0r0Fl7k07H52YnJUGYRqeDwSAIeO7kSZD74sV4nbtymdmMQi8pRkbwWtZuV1mJ64mNhcd47Bg+g1W62+3w9pcuDZx8e3rg/bPBIXl5RLt2+T7O6Ciq2hsaQGbLlwemj56Xh6LAykqsA0tLfOUr028T7OiAhrvNBsPt1CmkJFatgmPc0AD+nD8fhP/aa/g+cflVfqy4OLy2rw9/u89HZ8WBmthYWvj883Tp+HGqWrKENrovnsMBi8s9RyQI8NxnCDKRB4Dq6moSRZHy8/MpdKIRSDJkyJgUUoGVtWuxcXZ1Ef2//0f0zW/6btkSBITfAwmKVVZiv5Vu1omJaHVjni4TBrFYuAobC7cyjfOUFH7eCgW8zIoKRBHWruXV9CEhvI/avdqdFb+Nj2PYjEaDn+FhGDNRUQjtFhSAH9jo1q6uwIjcYkHu1+GAx8rmm7/1FtbXvUhuZIToP/4DHqpOB2I8dQok7Gt+SG8vSDM6mq/vgw/CAGhuxvXk5wemHFdbC6OpuxsO7ebNIOc9e7BOTLZjaAjed1ISBIl+9jN0gTHCdjjQ2lhU5N2IUCjweFERIiJMS99ux7F378bfS5YupUtVVXS5v582RESQ0NuLxYyLw4e7q7+xmbXT7TkMADKR+wlRFL+sVpfD6jJkTB8OB9rPkpL45puYCMI6eRK92MGCN0EVFh7X6yGT/cUXfH734CAMBVZ5LYrY4N29fqkgy8aN8BTLy+EJZ2aiit59Pw8PBzl9+ilIkwikr9fDCBgYAA/Y7a6OXqC+Q309jAOWMmCRBTbq011prrIS58NeHxWFsPiePcjdu3usH30EImXrWFIChTilEseYSk96bS0MjdhYhLuHhuCFP/UUIijp6fjeXLiAlITdDs971Sqsj9TrZiIv4eHIm0u9bquVr8d998GIuXEDhpcgYIBMXh5em5GRQXq9ngY7OqjlJz+hTJsNL4qNRU9gTg4ssrg4nJzRCIvCXXD+FkImcj/R2dlJvb29pNVq/R9vJ0OGDJ8YHcUG6t6epdN55pWni6VLUdQkCCBZVjGfkYHPu+ceENvhwwjzJybCI+zuBsH29KBAzF0vvaeHe/QKBdIFpaXYzycSxykrgzf/29/CGywsxOc7ncjNqtV8spnBgNcyj9FfDA97b00TBKy7O2prvd+L1lYcixkxo6OobTh/HhzG0gynTiEMv2pVYOcpxYED4D/mwbOBPMePc5W4pibUK8TEID0dGYn7NDjoOimOXWtWFoj73DmQusMBA2D3bk78zz+Pezkygs+XtgMKgkDFixbRsf37qSohgTJZn/jAANHvfw8loMuXUbmu0UBBaDqzZ6cAmcj9xOXLl4kIA1Lk3nEZMjwxNgbicB+tabOBrGprEWpl+hnSnmbpe8xmhJWDiSVL4AF/+CH31FQqz7B3UxM28vR0nO/p03Cutm4Fab39NoyMkBB44omJnmOoBcE/hbuCAqK//3uiX/8anqfFgjXMzQXhtLfjPNPTIX/rb197by9ISRRdh7YQ8aivt7z3vHkIh0tJzOHAe0NCeK7+5EkQq1aLc8rOxr8JCUgzTJXInU7XiACDTofHly2D8dDYCPIWRRBvcTGMjD17wK0sHTI4iHOcPx9dB8XFSKWEhqKmwV1Ze6JivCKdjo5ZLHTFbKbtDgeplUp8UEsLblRZ2awIwTDIRO4HRFH8snd88eLFs3w2MmTMPOx2OBznzmFzX74cPxoNiGPfPoQmFQpsktu3gxDGxxEqbWgAUdhsCOGyueIbNqDgLDkZxD4wAGIvLQ3u+TP1r82bsfkzEZFz5+BFx8Whql2v5+H0khJ4w7m53Ov+9rfRo9zbi3x5QcH0BrlERmJe+LlzqIzPzkZnU1ISPkOp9F+tzumEsXLqFO6DwwFCt1p5JXx/P79ed6xaBccyIgJk53TC82Vh6yNHkDZISwNBRkbiO8EGl6jVCMX7gtWK8wkL854+ZsYA63dnMJmQK9+2DUZeRQU+S6lEIWFiIs6Vbc2trSD5efOInnuOpyRycz09dn8RGx5OyZGR1OlwUKPRSPnMCmA6ubMMmcj9QFdXF5lMJtLpdJR8KwSdZciY4/j4Y5BNbCw23L17QTy7d/NK4vR0bKhMIevrX0c/dEODaz7WZkNotrAQqm0qFUiipwcb9mOPgRjsdhgH7e1wfhYsmHqvM6vaTknxfK65GZt+V5dnG1J0NDxAhvDw4EuwRkbCoNmwwfXxQNu1Ll/GlLisLO69K5Ug3XnzsM7bt3tW0TNkZ+N+7t/PPfkVK0CgDgeOnZoKEk1OhpETEcEV+AwG3974uXO453Y7jpubi89yV7TbupXojTfwPYqMRKTCZMKc8bAwtIuFheH7kp/PSdpggIHy8MNcGCgpafpjU79EcjIVREdT58AAXevuBpE7nV8+N9uQidwPXLt2jYiI8vPzSZihBn8ZMuYKurtRXCRt3YqIAEkfPcpnZBOBOFJTecTx+nXPzVqj4TVBaWkIXZeUuOaVrVZ48vX1IA5BACF97WtT60eeKBvGKsMjIuBcSQumzOYZrVmaFtgYVSl5pabiPnzve/4Vy61YgSrugQEYLSxXbbW6Tp9btAivGR7GD1OHKynxFPlpbSX64ANezS+KMI4+/hhCNVLk5yMicegQN6wef9w13L5jB6IVra24bw4HPnvLFtxnb8ZaoHBvR6PYWCq47z46/ItfUF1jIzmTk0lhNsNyCcYHThMykfsBRuTygBQZdyJ6elx1uRmUSniz3vLBrI1Wr/fszmHjR6WE6Z5XPn4coW6rFa+PjgYp7dtH9MILvs/VbkeeG3OlubOUlQUiM5u5YTE6is9kBVsbN4JwUlLw2pERkNVDD/m9VLMKb5X5AwMwht5/H6mQ/PzJ+7k1Gs8cekgIjK7+ftwLrRYRhEuXsMYbN8Iz//nPeXvgtm1Y6/Pnca9ZHYQgYI2vXkUem6UyGPLyeMW4N4SFwaBrbIQnHhODPPh0Z9WLItI+hw/ju8u6DliRYdyjj1L0lSvUf+0aten1lLF798QnOoOQiXwS9Pf3U09PD4WGhlIm09qVIeMOgq8eYKcTBNnW5vk4GzwSF4e8KiNQpxPCHrm5E7fZvvEGNtO4OJCT2YyN3+kEAXsLsQ8MQGq1txd/iyLIa9cuEPMzz0DNq78fz2k0kOlk17dyJY5/6BDvpX7qqannVWcaS5fC0GHX09iIfHJUFLzX2loQ7KOPTi3kvGMHquw7OnAvTSaszXPPoXh7bAzGligizN/Xh/SK2exJsswwdDfyiHBckwkE72uYjEo1OeH7C4sFBsmePSjKLC5GJKCvD3313/wmDBtBoaCCtWupQqmkuvx8ykhOxqIqldxSnCXIRD4JmDeem5srV6vLuCORkQGvq7OTV/r29MATWrIEvcS1tbzHt7cXuW9G1M8+C0+XFSEtWDDxZKrubq6sJg3l9/byAjBv2LPHtW/a6QSRsZnYKSlE3/8+rkMUQTrSvVcQEClduRKbe1hYEHOsM4AVKyAfW1+P6ztxAveorIwrx1VV4fqm0kGbloZRsZWV8IRXrkQleXMzjCipn8PSK21tCMPX1rqOFR0ZgVcvLeSz26ErcPo0r7IvLUXIPNj3QRRxDb290A+or4cnbrfDYFy6FAWOViuKB3ftwvsKCgqooqKCrh04QJuPHSPB6eRl/c8849mcP0OQiXwSyGF1GXc6FArsUfv3o2Lb6YQnptEQ/eIXvBp6cBAe8GOPubbR5uYS/fCH8HBCQiafS202gwhaW0G0bFMfG0MBk3t7GxGI4fp1XqwmiiiUqq3FxrxyJULPOTnIy3o7BgMrEJsuuroQVh4cREi7qGjiz50uNBoYTU1NRGfOYL2Li7k3zPimoWFqRE4EY+Dee10fGxrynV4xm1HUeOECPjciAoaV04nvlNQoO3UKKRVWrOdwoAYjOnryWfDuGB5GRIINwpFGfwYGiP73/4aRZzTy8L4owrBwOBBRCAsDoXd28vempqaSloj6z5wh4/btFM8sEbMZvYk/+tGtvck+IBP5BBgZGaG2tjZSKpU0f/782T4dGTJmDTodio66uhAqLy+HF1NSgo0yMxMeGJuk5Q6l0v8itbg4/Gg0ICUGrda3Jy+K/KelBeRdW4swfEYGH2954wbIdfXqgJcgINTWIoyvVsMYuXIFnuxXv3prI7BKJfLFISEgqkuXYOQkJIAg7Xb/Zp8HgsRET318pxP3IjYW9/G553BPrl+HIVdc7FlEeOwYoibSivuEBEQWAiHyujoMSWFhe0GA8bFmDc7p5z+HgZCUBONweBhGY3Q0l+nVaEDgCQmu3QQKhYLyw8LogiDQtb4+TuQREbCc2tpwA2YYMpFPgLq6OhJFkbKzsylkFqwsGTLmEkwmjNocHsYmp9XC0xobg+BGSgrCops3Ty8UqtcjrHn4MDxpqxVktGiRb331iAjsn2fOINQ7NIR9lVVI79uHDTkuDud8K4ncbudzyVkuPzoa53X5cuDe5VQwMABCI0KO/Pp1/CxejHsVTGRnY+1v3ICxxtIrJSXceFOrEZEoKvJ+DNaO7d4zr9HwwSb+wGLBXPl58/jaj48jmjR/PgyMykpuKLIqerUaxD82hsdFEcey29FVIUVBWhpdIKKr3d1UJk3SM4m7WUBQMg+CIGwTBKFOEIQbgiD8Fy/Pf18QhFpBEC4LgnBIEIQMyXMOQRAu3fzZG4zzCRYaGhqICG1nMmTcyRgaIvqHf4An3tAAkjCbsfFevw6yZXPCve1lNhuO4XD493lbtiAEnpaGn8cew/AO9yFTUtx/Pxyi4WHk2QUBJBYXh8fOn/dsjboV6O/3XpCn18Mr9YXRUS7gMh04HBCG2bABHiWTYx0bgzHkXiU+XSiVuFc7duD3sDAo0QWilS8IMDB6elwfNxq50Is/aGvjk8sY1GoYljdueLbRRUfz75RCgdQM+47Ex6MmwL0oM7usjFSCQF0DAzTCbtbYGPIL7kIEM4Rpe+SCICiJ6JdEtJmI2omoUhCEvaIo1kpedpGIVoiiOCoIwstE9G9E9NjN58ZEUZxZYVo/IIoiNd2M62VnZ8/y2ciQMbv485+xSTId6rExhLCZAtfoKDbJBQtc86VsAtWJE/BuIiMhSjLZ5iwIeE0gm3hkJDy+lhY+zGR0lPetW614btu2wK8/EISG8hY7FpkYH4cB1N2NNZSOB3U4oDFeUYG/lUpENVavxjq0tSGKMDwMsissnNgYGR4GeaenI7IxPMyNK28a68FASAhC12vWTP0YmzcjldLaCiIeHcV3bflyrN9ERhyDL5kP9nhiIsjbZMK/YWGo4aisxBrZbIj6JCZimIq3WgJVaiqlr1lDjceOUXN1NS2Ki8NNe+KJWatcD0ZovYSIboii2EhEJAjCu0T0ABF9SeSiKB6RvP40EbnJAMw99PT00OjoKOn1eopi4r0yZNyBGBxEeDo9HVrVRCAhoxHhYr0eodSYGChzSXH0KKqC09KwEY+OInf80kvBL/ANCYEX1dcHAyM5GcQwMIA0gMkEXXRf4d1gQacD2dbUoGjPbocx09UFYj17FqT93HMgkePHEenIyAAf2GxQztPrYXx88AH4QaNBrv3iRRS1+SK20FDX2eisHc1gcK0sn2uIi4ME7qVLMHisVnzvfvMbXDuTM58obZOWBnKW6gWw4rq8PDz34otEP/kJvotaLV5bUoIIwtgYIhZ33YUCRV/I2raNGm02akpKokUbNyK/EOiw+CAiGESeQkTSTtJ2IrrLx2uJiF4gos8kf4cKgnCOiOxE9C+iKH4chHOaNpg3npWVJau5ybijYbfDo0lPR3jSZAI5ZGTg93Xr4L0sWuRa7W23wxNnJE4ET0unw+CNyYh8YACk19oKUi4pmVhljRU1NTRgcw4Lg8EREYF9NjsbldIz8d/5gQfgldfUQFmtt5do0yYQOxHO7+OPobjGpE9ZBbdGg3DukSMwSqSV+tHRSGVcu+Y7WhEaCm++vJxLqprNICn3AS+zBbsdXrZUFIgI36u1azmBJyTgO2WzoTVNoZh4NklICHr/f/97nlsXBNwPlq/fsgUe95/+hHuzfj3kYgMxLLOysoi0WmpSq2d80pk3BIPIvf23EL08RoIgPE1EK4honeThdFEUOwVByCaiw4IgVIui2ODlvV8noq8TEaXPQB5CSuQyZNzJiI5GUs7+lwAAIABJREFUrtlmwyZ75Qq8O7MZ4x+ffdZ7+5HF4j0kGh4+eQFTby+mgtlsIP6ODpD6iy9yMvSGBQuIfvADotdfh9fLvOPMzJkjcSIQ1BNPoC7gP/4D5yXto46IQMi8txcE626ghIaioFCp9OxmioxEx8BEaYdNm3CtFRUI3ev1iABMtHYzARadqKjAdQsCSDUtjU/FI0KUQq/nhqFGg3MvL0dv+USSHllZaHdsasK1p6d7tjxOVHjnD5KTkykkJIT6+vq+nMMxmwgGkbcTkXRSbioRdbq/SBCETUT0/xHROlEUvyznEEWx8+a/jYIgHCWipUTkQeSiKP6GiH5DRLRixQqvhkKw4HQ6qbm5mYhIVnOTccdDoUDx0htvgJgzMuApFRaiJc3XyE6tFuQ1POyqDtffP/moyyNHsAkz4tHpQP5/+QvkOSdCdjbRP/0T8sGdnSCBtLTZEXfR6/HZ16+7Ps7as3Q6rCeTPmXo7UWEw1txnNU6cRS3thYV/2wIzZo1mNI2F8Rt9u9Hv3hSErxuJvFbUoI89YMP4vfeXs9iQY0G126zeXry7ggLC351vhQKhYIyMjKovr6empqaqNhXO8UMIRi3tpKIcgVByBIEQUNEjxORS/W5IAhLieg1ItopimKP5PEoQRBCbv4eS0SlJMmtzxY6OzvJarVSTEwM6SdTr5Ah4w5AejrCwPfdh5awsjI81tLiu+NGEPD6/n7uwbe389DvRKir86wWjo7mXpY/0GqRg87ImF0Su+suXLvFgr/ZeNBly0BW27fjuc5O1CO0tYGIduxAyxSbS04E48Tp9N2GV1WFYTMWC9IRvb3oqe7qmplrnQhmM6IqTP60p4fntMfG0L746ac49/nz8b2RwmTCdyJY9WTDw4iYTBUsWtskFTuYJUzbIxdF0S4IwqtE9DkRKYnodVEUrwiC8I9EdE4Uxb1E9D+JKIKI3r+Zb24VRXEnES0gotcEQXASjIp/cat2nxXIYXUZMjyh06Fg6PXXsckqlQiV5uUhL+mtkjovj+jll+GFGY3wDktKJm+BmjcPm7s0LG+xICQ9FzzLQJCZiYjGp59ykZLiYhA4Ebzmb30Loz67urA+y5ZhvR95hOjDD2HYsAlwzzzjXVxHFFH9zvLKRCC+nh6EpJ98ckYu1yfMZlyDUonvAvu+aDQgadZdwEaSVlcjpTJvHgyYsTG0IPqbHunoQHTC6UREgkn3GgxE//qviACIIiIfP/pR4Gp3UiIXRXFWa6mCIggjiuJ+Itrv9tjfSX7f5ON9FUQUQIPJzEAmchkyvGPfPlT7SjNOdXUgIV9edmoqCEkKux0EwxTf3PfAdeugeMmqtcfH4bHu2jVzee5gYvly5LT7++GBugf6vFX8E8FwefZZeOpWK4jZV37YasXrpCM/ifBZ7e3BuY7pYN48XpUfEsIjKxYLj76IItYnJobolVdgADY2wkNfs8b/HP/Jk5h/rtHg+3L0KPrqN25EZKmtDQZPTw+6KioqUJPBWv78QUJCAoWHh9PQ0BANDAxQtDQ3MsOQld3c4HQ6qe3mOCc5Py5DBofFgiKrtDTXx+PjvRO5KMIr6uiAhzh/Poi5qYnovffgoYki8qWPP+4aSl+8GPnSAwdA4koliM5dZet2gkbDh84ECn9EXDQa7r1KuwdMplmb5eGC0FD0iu/di2jD+Di8Y72e58yzs3m0IToa6YVAMDICY/NXv0JdRk4O2sgUCpC5xYJ0UGoqvssOBwo5jUai//W/8PdEVfFSCIJAmZmZVFtbS83NzTKRzyUYjUYaHx+nqKgo0gZjcoIMGX8lEATv3orT6VmZ7nSivaqykofCtVp45kyDPDYWOWKjEXnd73zH1dtctQqerMkEz1RWSZ4YCgWI8t13UQWv1cJDHx31n5xuNUpLQZwnT2IgSU8Pviv79uEeq1R47u67A0+h2O0YY3v5Mm9zvHEDa1Baiu/utWv4t78fhoS0Kl6jwQjbkhL/8/CpqalUW1tLnZ2dtMzbkIEZgkzkbujo6CAiopSUlFk+Exky5hZCQtCyw4ROiLAJ9/a6DpYgwoZ59ixC8GxD7u/H1KnmZm4QREcjH8zmTbgHwdRqT/1tGb6xZAnI8NAhhNMzMtAGN9ttZ1IsXMgryisriV57DSHv+HikB/buhUE3WWeDOxobEf1JSYH2gFKJ75fRCE0CUURkwulENEhqfDociAo4nSB+fyMnycnJRIQC6dmETORuYDeE3SAZMmRwbN8O0m1p4TMiSko8NTEuXkTIVOpV6XQYqqLVcsIeHkZ+Mjd3+hrjtwPq64kOHkRRW0oK+r1zc6d3TKcTEq4nTyJ0XFxM9MILwZ9yFkwMDaGI74MPEA4fGoJBFxODdTlyBN+rQLzygQG8nlW2j40h3y4IMDYjIiDPe+YMCg8dDqzd8DCIOycHof5A1i0pKYkEQSCDwUB2u51UvnoxbzFkIneDTOQyZPhGRATkVdlwkrg4rhkuhULBW6YYjEY8ziZOCQLymL292Mj/2v/L1dWhFz8mBh6yyYQOgK99berzwYmIPvsMI0ATEkBcJ07gs156aeqtWiMj8OgbGmC4paXxSvrpQhSRXjEa4RUnJCAsXlEBwyYsDIRqtwc24CYmBsSsUsGbP3sWUaDBQXzXnn0W37f//t9hSP7qVwivl5RAjKa9HYJHgRB5SEgIxcbGktFoJIPBMGuRXJnIJbDb7WQwGEgQBEpKSprt05EhY05CofCsjHbHsmXQzI6K4nlvgwHEn5mJ8HpICDbeoSFsplLRmLmCa9dQ1WwwoP95y5bJr90XvvgCZMMq1ufNA6l98UXgRG6xIP9rNBJ9/jmU49g6s/7+q1eRhw4E4+MwDA4fhpevUKDwsL4eRPuNb7gK10wFnZ0IgWdk4PfOTqzJ6Ch+j41FmDvQKXVZWbj21lZ42GVlOO/MTNRfsOOFhBC9+irRQw9BoKapCd77li1TqyVITk4mo9FInZ2dMpHPBRgMBnI4HBQXFyfPH5chYxrIy4OG9fHjPB8eG4vNNC8P3jeTIE1Pv/UTyaaCmhpodsfGItzb1wf975demtq0ys5Oz/cx+dlAj/O738FrHhiACIzDAcJloejQUHiYgRL5oUNo+errgxEWFgZVutJSpD7Ky9FNMBGYB+xLS4tJsxLhu9DVhfc4nRiWolKBZAOFUgmv+9gxXmT54IPwsr0ZBcnJiIawroip6hMkJydTVVXVrObJZSKXQA6ry5ARHLABJitWYKMOC4NntG8fcpRRUfh7YAAVylNty7pVkIqrsFBrdDTI5uhREMZEGB2FR1tfj/etXAniMJlcCc5kCqwQzenEsA+lEh5tTAyKvG7cwBqyNIfFMvGAGW+w2VDDkJIC4yAqCvcxPByfsWIFdPZ9EbnBgJw3M0yys0HI7sMj2b0eH0cUZv16nH99PWotHnlk6sV54eEwCgMxDP0ZjzoR5kLBm0zkErCKdZnIZcgIDuLiXAnlgQdQ3HXxIv6+775bq4k9Vdjt8EqnIq4yMgLPvbcX4fP2dniIpaWIUDCN9YEBkB9TePMHvb0Ip7PziogA6V2/jhBxXBye12qhhR8IbDZct1oND5b9rlLBi7ZYfHvZFgvy/aKIc2MaAr/7HUaTStsKIyKgCfDpp7zlTKfDUJcnn5x4IEqwYLHA+w8JgWExHZGhxMREUigU1NPTQzabjTSB5gSCAJnIJZA9chkybi2USoSAJ5rcNdtg2vAKhefAl6Ghyb3F8+dBuIxs9XqQe3U1JEaPHIF0aFcXWq7eew9h/J07XYVcvMFbL/+yZfBumZZ9Xh6iIYFWrWu1OB+TCcZWdTWiCWYzvOueHrSyecP163gdu2Y21aylBT/Z2a6vX7sWnv/58yDVbdtgeMwEiV+4gBY3VrWekgIDwh/RHW9Qq9UUHx9P3d3d1N3dPSPTOd0hE/lNOJ1O6rs5WzHBWxmuDBky/qrhdKLQq6ICRNTTg8rntWuRJx8aAlmtXz/xcerqPMPJWi08/Lg4okcfJfr3f0cluF4PY+HQIYSWv/td314vEc4jPh7HYv31goDisK9+FQVfUw0VCwLR/ffDsw4LA8HV18NrjYiAceBrWAvTUfeG0VHvj2dng/iHh+HB37iBx9PTPSefBQsdHUR//rPrjPfubhhTL7009eMmJiZSd3c3GY1GmchnEwMDA+RwOEiv189KaESGDBkTw2oFSRoM8Pby8oKr9nblCgqlsrLgjaenw0O8cQNeY3o68sM6Hbw5X95jVBTIQdqq5XCA6EJDYRw4nSDspibko0URXvrQEAjZV1hcEIgee4zozTe5sI4owrjIzZ2+Dn1WFga4VFYiRP/446ioT06euJUtORnXyNoKifioVl/1DzU1CK83N+Pak5NRNxESgs8tKJjetYyNYT11Om4YHDwI46SpCfUEWVk8cmA0Bl5XwBBz06rq7e2d3klPETKR3wTzxmNkGSkZMuYcTCai//xPhKzVaoSS4+JAesHobSYCwUZHu1YvFxcjXP3jH+P5P/4RuWOtFh6quxAOEVrpLlzggiQOB/ruS0pAKIODyEGbzSBxnQ55YkHA7++///+zd+fRTZ1pnvi/ryRL8r4C3hdsg9khmDVsgUBIZYGkSQJZqyrpdFVX969neqpOVU/P6dPTp+tMdc3Mr7p/03O6O1XpCkmaJBUSApUKSQhhx2BMILbBYIyxjbHBNt5ky7a29/fHo2vJtmTLlqwr2c/nHB8brc+rK+5z350Smrem8VmzqOZ+6xZd3KSlTTwBeTJz5vjXOM/Ops9KmXIoJZVz3bqR29EClDjffpuO6+nTlLwbGui9U1Np69Wf/GRii9ooAxJPnHBtsbt+PV0oHDpE75mYSN0BDQ20QY8Qrp3pJiLFWUhO5CpTDkCKp28dY0xVR4/S4DD3wWeNjXTCfvLJwLyHMg3JnVLjPX2aEkNWFl1I9PVRc6zDQX/39lLNVZnL/PzzlDTa2uj5K1a4BrXl59PIfaXJWaejZK+sStbcTIluwQLvser1tBlIIAwMUFN9VNTE+4mFAHbtolr05cv0OW7ZQp/LO+/Qxcfy5a7ugJMnqXXl/n3XoLr2dho1P3cuHYvaWloSeLwuXaK59dnZ9Lo2G83VN5mo1eLbb+nzMxjoO3XtGo178LQ1rK+UvKFUCIONE7kTJ3LGgk9JZmP1iV66RDVPd7Nm0e2BSuRLlwIHDw6t4d+/Tyf5sjL6rfQ/R0ZSDe6//3cauKfT0SC2pUspoS1cSEmts5PK5l6+oiJK+GfPUhLt6XEtrar06gVrq9YLF1zLlba3U/lWraKa9PBd7sai01H5ly6lcv/bv7kGC9bUUHn/+I+p7/3aNSp3fLyrhUKnowsfk4leT6lNA5SMBwbocxzrszlxgr4byrHS6egCoqyMpra1tdFc/IgIOoa3btGCMf5MQ0tMTIQQAh0dHaos1cqJ3Imb1hkLjqYmOnmeO0eJUqOhWtgTT3ivEUZEjOyXttsD20f+wAO0Glp1tWv6ldKE/pvfDF1UxG6nGqXSlw5QzfubbyghFxVRAvFUL4iIoKlWs2cD//iPlMxWrKDmcbOZ7g/GDsq1tTTvOyODatGnT9P7f/451U5/8ANqWZiIkyepNq58NomJdKz/8Afg9dcpISufL0BJ2+Ggz7i3lz7X3Fz6nE+epGl7Fgt1fTzxxOjr0ytLB7uLjqZavt1On3VLC4216OujdQz87Y/X6XRITExEe3s72tvbMdOf6v0ETHAtm6mHa+SMBZ4y/xigE+m+fcA//RPwN39DtV+lX7S2lgZw2WyeX2ftWhpxrKzfLiU1QY93h6zR6PW00Mv3v0/9pn/0R9QXnZNDCbm72/VYk4kGUrnXWpU+7itXxn4vg4HWFf/7v6fX7+2l5vTOTkqekzVq293581Rb7uqi2rLRSP3IERGUeN94g/qRJ6KqauRFTFISldFioVq/VkvlnjWLYujspBi6uqiVJSGBuk6++IKem51Nyf6tt0afyz9vHg1cc9fZSQm7sZGSeWoqUFBAvx95ZGJlHE6pBKrRvM41cgB9fX3o7e1FREQE4gI1coaxaay9nVZxq66m2tXChXRirqigJKXXU1N5ezvVbJcsoZN8XR2dYIdbv55qURUVlADsdmrCffDBwMat1VJtb3iN7/HHacOTvj6q3d27R48dHqvVSsnIaqVm6/PnKdblyymRDB/5vXQp9ZnX17tqocFI4gBdmBgMdOFhs7m6FKR0bWxz/Ljn2m9zMx0rvZ7uH37ajIujpnP38iqfjU5HiXztWnqd/n66gLBY6LX+83+mpnCLhWriyrgE5XX7+mgZ2Wee8VyuzZvpAuT2bRos19NDcf7FX1BZz5yhYxIfD7z44sSW2/UkJSUFN27cUGXAGydyDG1WF8HqnGJsihoYoLnIZrOrxnr1KlBeTgnZ/TwXG0sJQVkgprfX82vq9bQYyZYtNEApMdG/wUnjVVAA/OhHVHNtaaHadFoaJQmledhiobIvWUJN1pcvu/pqv/ySdhL73vdGDqiLjR3/KmyBsGABzZt3P+VZrZTEIyK890UfOULjAZQd7iIigBdeGJrw16+nQW4DA3TR099Pj33uOXpebCzwp39KrTKNjXTbkiU0IFC5kOnrcw2EcxcdTcfAm5QUmkJ38SK9dno6XUglJFA3wvLllMzr62mMhdE4csGaiVBz5DoncgDt7e0AuH+csUCoqaGatns/b0YG9XUq83qV3btMJkqAV67QCXysaVQzZwY3gbtLT6eBbIpVq4B333Xtza7RADt30u+KChrQpiTDvDzqPrh1y3OLgxqWL6dE1tHh2oUuIoJaCMxmKsf69UOf09BAO6Mpc+wBuvh6/32aoqeMI1iwgOb5//a39DpaLdWym5pcYx3S04Ef/pAuhnS6ka0VMTH0YzYPbaXo7KTavDuHg2Izm6m5PCkJeOihkWXu6aGm+Y4OV1N/ZSXV7h94wK+PczB/KPkkmDiRA+h2dn7Fj7akEmPMJ11dnhdLSU+nfu6iIqqldXdT4khOpmZoZa5vuEhKou0w79xxzeeOjqbE4GkpVa2WapKhksgjI2kUeUUFJeCjRymZKvuEv/wyJWN316/TY5Xja7HQILa6Ohost3Ej3TcwQE3bTz9NSdZgoJ9r16jZ231wmbe54lotzWfft49q8NHRdIFoNA4dG9HVRXPS7951TRdcv576vocfg0uX6DXc16qPiaHtTBctGlr7N5upXMr68cPjlJKO9dmz1HqQmxsPi8WVT4KJEzkAk3O+Q2wobojMWJhJTR05aM3hoCSdkEC1N+VcpzSfbthAtbLu7sAt8BIMGs3IaVpxca5BeQqbjboUzGb6O8izk7wyGmkU94oVdEFy7hzVmIuLh7YoKJTmdICO1Zkz1LrS00ML2dTXUzP73btUzuHJLypqZCIfzaJFNMr99Gn6/FaupNq4++yGAweGJme7nZr+c3Jo4Ju7mpqRMyOMRrrA6upyDdCrrqZFaZRFYoSgMQ7Z2dRdMnMmXfgcOULPiYgAzp+PweXLwMqVPZBSBrWbNkS+TuriRM5Y4OTm0nSy69epqdzhoFremjVUKzt+nGqDCQlU0+rupubZ6OjwS+SeZGZSErl9my5eWlqozDodnfzLyijZjXeetif9/ZRsYmP9n3uekUEj9Uczfz6VwWqlMQAOByXnyEhavKW6mqbg5eaOvJgB6HljbQwzXF4e/XhiMlFydv8stVoaQ1FWNjKRJyfTxYZ746uyfK7SfG82UxKPj6fbzGbqFjp2jFoCDAYqa0UFlVNpncjLi8C5c5G4e7cPZrMZ0eMtqB94+hk4kTMWSBoNTaF64gnXcqpr1tBAtW+/pVpWbCydKDUa+t3QQCf+pCS1o/efRkOjoZcvp6bZr76iRPP445SQdDpqCh4YmPh7DAzQynE//znwy1/SlL66ukCVwLu0NNqKtr6e+vstFkqEynSy5GRqvp41i8rc3Ox6rtlMx3giq7V542l997t3afrbpUtD3x+gGr3V6lp0xmaj796KFa5EXldH5VL+ffkyPSc+nmrv2dm06Exr68gupJiYWHR1uXJKsHAiBydyxgJNr6cBT1otNbuWlQH/83/SKOK0NNea41YrneBNJpo2FKypV5MtKooGvu3aRVPk1q2jWitALQ5K/+tEHTpEzeDp6ZRYrFaaKRCMAdOrVgH/5b/QSPvVq4Ft21y7vSmLughBG5+kpVHSb2igVpcXXvC8SM5ExcfTZ3D/Pr33xYvU3F9bS9+7//N/KKErUlNpK1mAYrp3j/rTH33U9Rj3loT+fmpRiY+n26WkC7UZM4aua6DQaGIRFRX8RD7tm9allJzIGZsEH39MJ0Gl79JqpVrczZuU2G7epFHMfX1Ug/c0yjgYWlup1tXU5GqqnjmTkpT72u4T4XB43yXN2+I3Y+nqopaN7GzXBi/x8ZS4vvmGEutkmzWLjtfVq67+foeDEqqSFBMSqH+7tZWO/cyZvo8NsFrp+9HZSUlT2ZFuOCGoO+Df/50+k6oq6pcvLASWLaPP+OBBamJXRsUrc9V7elyD8Nzl5NAx6++nlg+Hw9X8rlyExMRQV0RDA/3Waqns0dGxmDWLE3nQ9fX1wW63w2g0IsKfxXYZY4M6O+lEnJZGtfDubuobzcujmplSy4mLoxPr7t3e+3h7e+mEmpDg+WTuj9pamo5ktVIi6OqiJLV4MdXk9uzxvge3L3JyqNbmvrys1UplnWgfeW+va7qbu8hISibB8thjdJyV6XcOBw1aHL7Zy3h3Zuvupmlr9+5RGe12mhL34ouet1JNTaUV+N58k5JvQQE18SvT3mw2amJ372fXaLyPxYiJoXL87/9Nsdy7R5/t9u10n5Q0uO7736cWEGVb2uxsYOfOWFy9yok86Lg2zljg2WxUsz15kprNldXYpKQ+1qeeopOh0jTqSV8frQ5XXk6JIj6epjMFYvEOgE6+H39MJ/R79+i2vDxKhn19FNenn1Jimugo89RU6jI4epSanKWkz2bHjokP6ktOps/TYhm6/nt3NyW8YImNpRr3nTt0cTFjhmt3M3988QXN83Zfh6C2llZz89ZqExVFYy887SmurFTnq44Oap5fuZKOVXc3XdRVV9OYDynp4q64mL4XjzxCj4uMBEpLOZGrQpnzx4mcscBJSqJE3dY2dNeyujpXrXfWrNFf4+OPqak0M5NqUCYT1Z7//M8Ds/92Zyf9ZGfTxYLShx0VRTW4/HyKv7PTv37dhx+m6VbKJivz5lGCnyi7nfrdv/rKNQDr/n36PJUV8oZzOKiMFy5QeQB6Xm4udSFM9PP0NP3OHzYbxZmeTrVrjYYuVmbNonEWDz1Et1+9Si09M2ZQmWNiqM/+6FHXPvAAXaClpo7cOW80ly9THEq5rFb6KS2lVqU1ayh5Kxd3ERGu+edKHuFEHmRm5z6KwZwqwFi4sVqplnL2LP29bBmdVL1d/2o0lMybmiihK02c+fmUyB2O0ZvJ29vpZJ2d7WpyV6aqXb4MbN3qf5mUWprDQUnt9m1KAA4Hxa60IIx3AN7AANVQY2NdJ/jMTPrxh9lMLQTl5a7bNBqKfds2qiEqCWy4Tz+l46fXu/ZCz8qiC5WLF4E/+ZPxJbv+frqwio8f2irgLyGo71pZBRCgPuiCAvosTSbaia6tjcra30/Twl57jfrg9+yh5XFbW+nYpafTbZ66bVpa6HOYMWPolDjltQF6jdJSer2ZM+liob2d+uT/7M9GNvUreaTX21rDk2TaJ/IB5xwQQyD3Q2RsivnoI+pDTkujpFxWRgPXfvhD7yfyWbNoNHNnJ51wU1Kon7u9few5z319lKSGP85goOcHQnQ0NZEq6243NFAty2qlWBsaqLbqayJ3OCipnDzpWs1s2zZqog2E3/2Oxh2kpNCKYrW1dHH01FNU4/dWF2ltpRHueXmUxKOiKCm1tbmO3ZEjtJKbL2U8epQ2M5GSvgtbt9IiLYFY/6Sjg75X7e2u3c6amqj2/V//K71vVRUl9L4++j7a7bT16ssv0zz3wkIa9HfjBn0mbW1Dx1eYzfRZ3rjhum3bNtdytLm51JSekkIXEy0t9HyTibpD9Hr6vlRXj5xKp+QRi7KSTJBM++lnygfOiZwxz1paqBaYm0s1kIgIql3eu0fNxd6sWUNJPC+P+plnznRtPTrWST8lxdUP7K6nZ/S9qMfrscfoRG+xUM1Po6Gm2Fu3aKCa+7SksZw5Qwlx5kyq7cbF0QVQVZX/cba0UOLIzKTm8bt3KYnFxlLLxZtvUoLypLWVyqXR0N9Kwtdq6fgkJ/u+XenZs5TIU1OpjCkpNBWuosL/Mp45A/zsZ/S9am+n9ffb211T2nJyaMxEbS0dL6UVRdmQR5kFUFYGfPIJLRRTWUm1508+cU0V+/RTui87m8qQmkr7pCufwaJFdBHa0EDvb7HQ76Ii14WPTjdyq1QA0DsfMODPIgETwDVy5weuD2T7EGNTSEeH59qxXk8nXW/9sitXUsK5eNE1qnnhQt+mmRkMtBPWgQPU/6nXUxyZmSNHRU9EWxvV9Hp66GS+fLlrERC73ZXgfD0tOBy0SEhGhqs53Wik1zh5cuQKY+NlNlPi7ehwbfgB0G16PTXlX7vmeeOP6GhXEouMpHIaDBRzZCTVbJV54KORksqSnu7qH9brqWn65En/Fnq5do0uCJTXy8ujQXSJibTVq8lEx+rWLbpAUpq+ExJofIBysWIy0brpmZmu4+Bw0MXP8uX02uXlrou1hgb6DBMSaDBdYSEdt9deo1aMc+fo38XFQwdlWq2eB2mqVSOf9omca+SMjS4hgU6G7itoAXQyG23Amk5Ho8w3bnSNUFd2LrPZ6MfTdCLFypV04i0tpRP0unXUN+/Pf1UpaZDY8eP0754eOrF/5ztDk5kyxctXNhslxOE7s0VGugaX+UMZjDa81m210sWClNSf0snnAAAgAElEQVQ6YjRSLdk9jqwsusC4c4c2QblwgRJmVBSV+e5d2l50LHY7fS7DR6ZHRtLFhT/OnqWLk6goSrAaDSVKk4kuREwmOu4ZGdTMHhnpOj4DA67pZvX1FKf7TGKNhv5965ZrYZeyMip3TAx9txsb6XlK90J0NK1EuGULtaqUlroupu7dowsFT5vfuNfIg7ne+rRP5NxHztjoZs2imnRFhWvxi+ZmShjDd8fyJDnZdfK3WKgfuaSEklBODi1d6m0K2mjrbE9EbS01DSuLfkhJt504QUvKCkEndJNpfDVMvZ5O7spe6Yq2NqpRjpfJ5Jq/nJ5OiWXbNmD/fkqmRiNdOCQl0ft9/jm915UrlJhWrACefJLKqNEAL71EzdJXrlCTvDJa32Sixy1b5jmGujr6THJzKenNnk1xuY/ib20d2SojpWvddYeDxiLMn+99gGN3N32GcXF00dLa6trC9OZNutBKT6cfo5GSsrLTWVISre3/z/9M3RhXr9Jr5uQMXbo1MpISuRCU8DMyXO9vNtPn2tY2cobCjh30vufO0ViPhx6iMQGelh3R6XTQarWw2+2w2+3QBWl3nGmfyJUaOTetM+bdrl2U0M+doxrQsmVUWxnv9e/vf09N7RkZVGO/fx/49a+Bv/iLkbtSTYbyckqKyuIsQtDiH599RglA6T/esGHsvnizmfp1v/2WkpAymKyvj5JQdzd9Phs2jC/G48ep1QCgRJWVRSvfrV9Px+CNN+iiKj+f7jtxgt5/7lxK0FLSoLCcHFdTe2wsvUZfn6vPWdmoxlNC+vZbqokqI/cjIqjWvn07Ha87d1xlNBqBTZuGPv/zzymuuDj6jMvLqYXl6ac9t3QsXEjlzs6mJWAbGuhCIC2Nmrnnz6fnrV9P+6Fv2kQXgsro+aoq+k4tWkS169OnKe68PNd+50VF9BpLltDn09FBt1ssdKGZlkZjEYYncp2OxnusWePb8TMYDDCbzRgYGOBEHixcI2dsbHq9q6lxorq6aDSw+9Kiyck0YOn4cUoWTU2UnFaunJwNVByOkYkkPp4G4D36KCWetLSx57hbLDSIqrmZmrFtNkrqCxbQBUlzMyWMFSvGd4FSU0NJMDvb1Q/d1ERz6r/7XWoB+eUv6aLj6FGqHet0dNHx1VdUPoDi+f3vR/aZu09P8xZXVxfV/GfMcHV99PUBH3wA/OQnNO3qwgUq4wMPUP+x+25ibW2uCwnlgikxkS7gVq70PO989Wpq7lamnQlBn8FPfzr08Q8/TM3vJ07QhVRenmutfiWGDRuoqb6khL5nMTHUZK7cP2cO9ZdrNPTclBTqM79zZ/w7s3mi1+thNpthsViCNq2ZEzkPdmMsKEwm1+hpdxYL8O67VCuLiaHEfuECzW0e3ufsq54eqplFRFBCUGqdixZRf2diItW+7t6lml1WFvXB+7oE7PXrlGDdVx+LiqJBWz/+sW+Dxzy5cIFqz+4VubQ0GlGtbPEqBJWtpYUSd0MDjc6eN8+ViEwmah3o7x99HIInt25RTdz9eZGRdHFQV0fHabTR/M3NFKP7GvPKcb9zx3Mi1+no8RERlHANBnp8Q8PQx2s0dJwefJBi1OmA//W/hq5nEBtL3RBVVXTxo+w4p5g713XxVVhINfe7d6lGH4jFbZRKYTBHrk/7RM6D3RgLjqQk1xKl7ifWyko6gSr95HFxdGI9dsy3QVjDXbhAI6CV2mlsLPDKK5QQCwupf/PXv6YBeBERlEBiYqj/eHhfr9VKNbuSEkocDzxANb47d0YmSGVk//37E0/kAwMjl4NV1lVvaKDkVFlJNfLVq6lslZWU1JXBbIBr45f6ekpc4+FpH3Fvt3d1Ue24ooKS/YMPei+7lN5rvBUVdDzmzqUm/8hIKtuXX9JnPnyhGyFcn1NODn0u7qvl9fbSd6qgYGQLjNEIvPoqfUdu3aLb5s+nMRKBWMtfqRQGc+T6tE/kdrsdAILWl8HYdGIy0WAlm41OuJs3U9NxSgo117e0UPIaPqUsOZn6SMfr7l2ashYfT4nN4aBk/PbbVFPWamnAVm4uDWaLiKAmZLudnjd37tApZx9+SEkmNZVO8qdOUXmKi0fOcQcoWcXEUCIxGMa/RvvixbRYiXsyVFbC27ePElptrav5euNGKk9NDV1AtLRQGWfOpAsX5WJmPHJzqazKWu4dHa4lUWfPpib5zExqlv71r6mlYOZM+pw//phqzElJFIvSotLeTknc00hvgI71jRtDZwvExtJnefo09Zu7r02vzO2OiqILq8pK6mZITKTX6OigAX7eBo3PmEHJvKeHyhrI7XOVXKLklmAISPYSQmwH8E8AtAB+I6X8xbD7DQDeBrAcwH0Az0kp65z3/RWAVwHYAfw/UsovAhGTr6TzMjNY0wQYmy6qqyn5WK2u27ZupV2szp6lk+j69ZQshiecvr6JDX67coVqWZcuuRYIiY2l2tmzz1IzqzKIavj64q2tlHyUpVSbmylB5Oa6EkJODjUvr11Lr3v3LiUrh8M173nfPkqqBgMltY0bvW9lOtyiRfSeVVX0fJuNLjZ0Onq/uDiqZSck0OdaU0PJNSeHElhhIZUtJoaS2US2YU1MpL3UP/mEBs9dukQxrF5NyfJf/oU2S7l3b+h76PX0WZ0/T0nyyy+pFUFKuhDatcv7ErL37g3docxkohHvOh2V9cQJGj2+YgX1tf/hD1R+Keni53vfo4GYtbV0PP7oj7xfNLiLiRn/5zMWJZdIb00bk8DvRC6E0AL4vwC2AmgEcEEIcUhKedXtYa8C6JBSFgghdgP4BwDPCSHmA9gNYAGAdABfCSHmSCmDdinDiZyxwOvvB95/n07CSm3HZqOT+5//OfV/KxISqDas9GVbLJRUn39+/O/b2EjN4PHxrjnDvb2UvKurKVFERQ29uFBIObS53NtCODodXYS8+iqNdq+upkQ9Zw7VXGfMoORmsVB5pfR9kGBEBPDCC1TrVxY/ycujqVVKjTQzk8oZF0cXHkuWUDK/eZPKbDZTK8dzz028pllcTInwV7+iGQqFha4k3N5O5UpOHvn6Wq2rK+BP/oQeq0wRG+0U291NFypmM13AKHPJIyPpvW02urDQamkgXloaHSuHg0bY63S0FW4oCMtEDmAlgBopZS0ACCHeB7ADgHsi3wHgb51/7wfwz4JKuwPA+1LKAQC3hBA1ztcrCUBcPuFEzljgNTZSMnE/0et09KPUiBUrV1IN/MQJ12IeO3ZMbKWw5mbXJigAJQ+DgZLynTt027Jl1FzrvktWUxMlTPepR/HxnpumbTZKYikpNBraaqWk8/HHVMNTEq5eTy0Bp065Wh58oVwUKP3dNhs9V2nqTk2lmu+1a64aelYW8KMfudaoLygYOpJ8IhISKAkvWDC0RSExkd5zwQKqNbtzOOhHeW9fZx5ERtL0rmvX6FiYza758wCVWwiqicfEuI6vRkMXNt98Q1PjAtlEPlFKLnFMpF9jggKRyDMA3Hb7dyOAVd4eI6W0CSG6ACQ7bz837LkZCKJgXjUxNl14uy6WcuSAIo3GtchGb69rSdaJ0Otd/aTKgiEaDdWSlf7q1FTaEeuTT1y7ZOXlUdO7u/R0SqY3btDfGo2rKd292VYZEe++jrn7fTYbJaaJlkmno37gzz+nhB0RQXOitVr63ObOpXi8NVv7Y+ZM+izd+6d7eugiZvFimjaofCY2G10sjXfKHUAtAEeP0vzw27dpKppOR+VVvi9CUJP78JkMykXG8AtHtYRrjdzTf9nhJfD2GF+eSy8gxOsAXgeA7Ozs8cTHGAuyrCxKLD09rn5Ii4Vqa95GURsM/i2/ClDt/sgRSirKFKiICGq6ffBB1+MWLqQ4WlroPT3tNy4ENdceO0b9vnY7rdK2davnpJyfT3PJ3ftdzWZK7t62e/XVhg30/qdOUdmio6mfeskS/153LFu20B7wWi29Z28vXbC88AKV8/XXqZn96lX6HLduHf8COAAdm1u3XDu6KfO7lTXqrVYq/7p11Bc+/MJC6UoJJcFs5Q1EIm8E4D77LhNAk5fHNAohdADiAbT7+FwAgJTyDQBvAEBxcXHALnXUuHpibKrT62lQ2zvv0MAvpWa8Y8fE54b74oEHqBn7+HHX+ucOB223mp8/9LEREUOX6fTEaKQ509u3e25NcLdqFTXxNjZSk7LZTBcQe/b4PtjNG42Gkur69a6V4/x9TV/Mm0djFZSBa/Hx1PeuTNNLSaH7lYV2Jpq7jEbg+9+ngYT371NLw5kzNAhOWeP/sceoW6Sujn7i4mgshs1G0wsDMXUsENTorg1EIr8AoFAIkQfgDmjw2vBhKocAvALq+94F4GsppRRCHAKwTwjx/4IGuxUCKA1ATD7jRM7Y5MjNpZXAbt2ik2129uTXmqKigP/0n6hWqOy9vWWLb2vCj8aXJJWQAPzgBzQi/8YNapV48EEaiBYoev3Em+gnaskSakYfGKD39pQwA5FENRr6rJTP68EHXTX03FxXq8nrr9OSr9XVNFZh+fLJvTgcr7BM5M4+7z8D8AVo+tm/SymvCCH+DkCZlPIQgDcBvOMczNYOSvZwPu53oIFxNgA/CuaIdYATOWOTyWj0fwvP8YqKoibYdeuC+74A9c8/9ljw33eyCTH+FeL8FRfnecMZo5G6UFauDG48vgrLRA4AUsrPAHw27La/cfu7H8AzXp77cwA/D0QcE8GJnDHGWKAoo9WDmchDpFdBPRHOIadWTxNLGWOMsXFQckmEp23lJsm0T+RqLHDPGGNsalJj/45pn8iVBe45kTPGGPOXGjtqTvtErlw1BXOnGsYYY1MTJ3IVcI2cMcZYIEgpuWldDVwjZ4wxFghWqxVSSuh0OmiCuELNtE/kXCNnjDEWCGrUxgFO5FwjZ4wxFhBq9I8DnMi5Rs4YYywguEauEqNz3cH+/n6VI2GMMRbOlDzCiTzIYpx7Dvb09KgcCWOMsXCm5JEY971sg2DaJ/JY50bBJpNJ5UgYY4yFMyWPxPq7Af04TftErlw5mUwm3jiFMcbYhHEiV4nBYIDBYIDNZuN+csYYYxPGiVxF3LzOGGPMX0oOiYuLC+r7ciIHJ3LGGGP+4xq5ijiRM8YY84eUEt3d3QB41LoqOJEzxhjzR39/P2w22+C4q2DiRA5O5IwxxvyjVrM6wIkcABAfHw8A6OjoUDkSxhhj4aizsxNA8Ae6AZzIAQDJyckAgPv376scCWOMsXDU1tYGAEhJSQn6e3MiB5CUlAQhBDo6OmCz2dQOhzHGWJhRKoJKxTCYOJED0Ol0SEhIgJSSm9cZY4yNG9fIQ4Dy4SsHgzHGGPMVJ/IQwImcMcbYRPT396O3txcRERE82E1NPOCNMcbYRCgVwOTkZAghgv7+nMiduEbOGGNsItRsVgc4kQ9yT+S8nSljjDFfKS25nMhVFh0dDYPBMNjXwRhjjPnCvWldDZzInYQQSE1NBQA0NzerHA1jjLFw0dTUBACDOSTYOJG7SU9PBwDcuXNH5UgYY4yFg97eXnR1dUGv13ONPBQoiVy5umKMMcZGo+SLtLQ0aDTqpFRO5G4yMjIA0IHhAW+MMcbGorTgKhVBNXAid5OYmAij0Yienh7e0pQxxtiYlBq5UhFUAydyN0II7idnjDHmEynlYCLnGnkIcW9eZ4wxxrwxmUzo6emB0WhEYmKianFwIh+GB7wxxhjzhXv/uBpLsyo4kQ/jnsh5wBtjjDFvQqF/HOBEPkJcXBxiYmLQ19fH664zxhjz6vbt2wA4kYccIQTy8vIAALdu3VI5GsYYY6HIarXi9u3bEEIgJydH1Vj8SuRCiCQhxBEhxA3n7xG9/UKIpUKIEiHEFSFEuRDiObf73hJC3BJCXHb+LPUnnkDhRM4YY2w0DQ0NsNvtSEtLQ2RkpKqx+Fsj/xmAo1LKQgBHnf8ezgzgZSnlAgDbAfyjECLB7f6fSCmXOn8u+xlPQCiJvK6uDg6HQ+VoGGOMhRqloqfkCzX5m8h3ANjr/HsvgJ3DHyClrJZS3nD+3QSgBcAMP993UiUmJiIhIQF9fX24d++e2uEwxhgLMVMpkc+SUjYDgPP3zNEeLIRYCUAP4KbbzT93Nrn/Sghh8DOegOHmdcYYY5709/ejqakJGo0G2dnZaoczdiIXQnwlhKj08LNjPG8khEgD8A6A70kplfbqvwJQBGAFgCQAPx3l+a8LIcqEEGWtra3jeesJ4UTOGGPMk/r6ekgpkZmZCb1er3Y40I31ACnlw97uE0LcE0KkSSmbnYm6xcvj4gD8AcB/k1Kec3ttZePvASHEbwH8eJQ43gDwBgAUFxdP+gRvJZHX19fDbrdDq9VO9lsyxhgLA6HUrA7437R+CMArzr9fAXBw+AOEEHoABwC8LaX8cNh9ac7fAtS/XulnPAETGxuLGTNmwGKx8CpvjDHGBk21RP4LAFuFEDcAbHX+G0KIYiHEb5yPeRbABgDf9TDN7D+EEBUAKgCkAPh7P+MJKOUg3bx5c4xHMsYYmw56enpw79496HQ6ZGZmqh0OAB+a1kcjpbwPYIuH28sAvOb8+10A73p5/mZ/3n+yFRYWorS0FNeuXcOmTZvUDocxxpjKrl+/DgDIz8+HTudXCg0YXtltFHl5edDr9bh79y46OzvVDocxxpjKrl27BgAoKipSORIXTuSj0Ol0KCwsBOA6eIwxxqangYEB1NbWQgiBOXPmqB3OIE7kY1CuujiRM8bY9FZTUwO73Y7s7GxER0erHc4gTuRjKCwshEajQX19Pcxms9rhMMYYU4lSoZs7d67KkQzFiXwMRqMReXl5kFKiurpa7XAYY4ypwG63D+aAUOofBziR+4Sb1xljbHqrq6vDwMAAZs6ciaSkJLXDGYITuQ+UZpSbN2/CarWqHA1jjLFgC8XR6gpO5D6Ii4tDRkYGrFYrampq1A6HMcZYEDkcDk7kU8GCBQsAAOXl5SpHwhhjLJjq6upgMpmQmJiItLQ0tcMZgRO5jxYtWgQhBKqrq3n0OmOMTSOXL18GACxZsgS0NUho4UTuo9jYWOTn58Nut+PKlStqh8MYYywIBgYGUFVVBYASeSjiRD4OykH89ttvVY6EMcZYMFRVVcFqtSI7OxuJiYlqh+MRJ/JxKCoqgsFgQGNjI9ra2tQOhzHG2CRTKm6hWhsHOJGPS0REBObPnw+Aa+WMMTbVdXV1oa6uDjqdbnDAcyjiRD5OylVZeXk5pJQqR8MYY2yyKOf5oqIiGI1GtcPxihP5OOXk5CAhIWHwSo0xxtjUI6UMi2Z1gBP5uAkhsHjxYgCuKQmMMcamljt37qCtrQ0xMTHIz89XO5xRcSKfgGXLlkEIgStXrqC3t1ftcBhjjAVYaWkpAKqNazShnSpDO7oQlZiYiMLCQthsNnzzzTdqh8MYYyyAenp6cOXKFQghsGLFCrXDGRMn8glauXIlAODChQtwOBwqR8MYYyxQLl68CLvdjrlz5yIhIUHtcMbEiXyC8vPzkZycjO7ubt7elDHGpgi73Y6ysjIArgpbqONEPkFCiMGDrPSlMMYYC29VVVUwmUyYMWMG8vLy1A7HJ5zI/bB06VLo9XrU1dXh3r17aofDGGPMT+fPnwdAtfFQ3CDFE07kfjAYDFi6dCkArpUzxli4a25uxu3bt2E0GkN+7rg7TuR+UprXy8vL0dfXp3I0jDHGJkqpjSutreGCE7mfUlJSkJ+fD6vViosXL6odDmOMsQno6elBZWXlkPFP4YITeQCsXbsWAFBSUgKr1apyNIwxxsbr7NmzsNlsmDt3LpKSktQOZ1w4kQfA7NmzkZGRgd7eXq6VM8ZYmDGbzYNTzjZs2KByNOPHiTwAhBCDB//MmTOw2WwqR8QYY8xX586dg8ViQUFBAdLT09UOZ9w4kQfInDlzkJqaCpPJxJupMMZYmOjv7x8c5LZx40aVo5kYTuQBIoTA+vXrAQCnT5+G3W5XOSLGGGNjKS0txcDAAPLy8pCVlaV2OBPCiTyA5s2bh5SUFHR2dqK8vFztcBhjjI3CYrGgpKQEQHj2jSs4kQeQRqMZ/DKcOnWKN1NhjLEQVlZWhr6+PmRlZSE3N1ftcCaME3mALVy4EImJiWhvb8eVK1fUDocxxpgHVqsVZ8+eBUC18XBZjtUTTuQBptFoBvvKjx8/zn3ljDEWgkpLS9HT04O0tDQUFBSoHY5fOJFPgiVLliA5ORn379/neeWMMRZizGYzTp06BQDYsmVLWNfGAU7kk0Kr1eLhhx8GAJw4cQIDAwMqR8QYY0xx6tQp9Pf3Iz8/P+xr4wAn8klTVFSE7Oxs9Pb24syZM2qHwxhjDEBHRwdKS0shhMDWrVvVDicgOJFPEvcvSUlJCbq7u1WOiDHG2NGjR2G327F48WKkpqaqHU5AcCKfRFlZWZg/fz6sViuOHz+udjiMMTat3blzB5WVldDpdNi8ebPa4QQMJ/JJtmXLFmg0Gly6dAktLS1qh8MYY9OSlBJHjhwBAKxatQrx8fEqRxQ4fiVyIUSSEOKIEOKG83eil8fZhRCXnT+H3G7PE0Kcdz7/AyFE+Ozk7qPk5GQUFxcP+RIxxhgLrhs3bqCurg6RkZGDU4SnCn9r5D8DcFRKWQjgqPPfnvRJKZc6f550u/0fAPzK+fwOAK/6GU9I2rhxIwwGA27cuIGbN2+qHQ5jjE0rdrt9sCK1ceNGGI1GlSMKLH8T+Q4Ae51/7wWw09cnCpq4txnA/ok8P5xER0cPXgF+9tlnvM0pY4wFUUlJCVpbW5GUlITi4mK1wwk4fxP5LCllMwA4f8/08jijEKJMCHFOCKEk62QAnVJKJas1Asjw9kZCiNedr1HW2trqZ9jBt2bNGsyYMQP379/n6WiMMRYknZ2dOHHiBADgscceg06nUzmiwBszkQshvhJCVHr42TGO98mWUhYDeB7APwoh8gF4WkpHensBKeUbUspiKWXxjBkzxvHWoUGr1eKxxx4DQIsRtLe3qxwRY4xNfYcPH4bVasXChQuRn5+vdjiTYsxELqV8WEq50MPPQQD3hBBpAOD87XFYtpSyyfm7FsBxAMsAtAFIEEIol0eZAJr8LlEIy83NxZIlS2Cz2fDZZ59BSq/XLYwxxvx07do1XL9+HQaDAY888oja4Uwaf5vWDwF4xfn3KwAODn+AECJRCGFw/p0C4EEAVyVlsWMAdo32/Klm27ZtiIyMRE1NDa5evap2OIwxNiVZLBYcPnwYALB582bExsaqHNHk8TeR/wLAViHEDQBbnf+GEKJYCPEb52PmASgTQnwLSty/kFIqGeynAP5SCFED6jN/0894Ql50dDS2bNkCAPj88895HXbGGJsEJ06cQFdXF9LS0rBixQq1w5lUfvX6SynvA9ji4fYyAK85/z4LYJGX59cCWOlPDOFo+fLluHz5MhobG3Hs2DFs375d7ZAYY2zKaGlpQUlJCYQQePzxx6HRTO21z6Z26UKU8uUSQuD8+fNobm5WOyTGGJsSpJT49NNP4XA4UFxcjIwMr5OhpgxO5CpJTU3F6tWrIaXEgQMHeG45Y4wFwLlz59DQ0ICYmJjBbsypjhO5ijZv3ozk5GS0tLTg2LFjaofDGGNhrbW1FUePHgUAPPHEE1NuBTdvOJGrKCIiAk899RSEEDh79iwaGhrUDokxxsKS3W4fbN1ctmwZ5s6dq3ZIQcOJXGWZmZlYt27dYBO7xWJROyTGGAs7p06dQlNTExISEqbdAGJO5CFg06ZNSE1NRUdHB7788ku1w2GMsbDS1NSEkydPAgB27NgBg8GgckTBxYk8BGi1Wjz11FPQarUoKytDTU2N2iExxlhYsFqtOHDgABwOB1avXo28vDy1Qwo6TuQhYtasWXjooYcAAAcPHkRfX5/KETHGWOj7+uuv0draipSUlGkzSn04TuQhZO3atcjKyoLJZMIf/vAHXoudMcZGUVdXh3PnzkGj0eCpp55CRESE2iGpghN5CFG+jHq9HpWVlfjmm2/UDokxxkJST08PPvroI0gpsX79+mmx8Is3nMhDTFJSEh5//HEAtP0er/rGGGNDORwOfPTRRzCZTMjJycHGjRvVDklVnMhD0OLFi7F8+XLYbDZ8+OGH6O/vVzskxhgLGSdOnMCtW7cQHR2NXbt2Tfm11McyvUsfwh599FGkpqaivb0dBw8e5P5yxhgDUFNTg5MnT0IIgV27dk3p7Ul9xYk8ROl0Ojz77LMwGAyoqqrC+fPn1Q6JMcZU1dXVhY8//hhSSmzatGlaTjXzhBN5CEtKSsLOnTsBAF9++SUaGxtVjogxxtRht9uxf/9+mM1mFBQUYMOGDWqHFDI4kYe4efPmYc2aNXA4HPjwww9hNpvVDokxxoLuq6++wu3btxEXF4enn34aQgi1QwoZnMjDwMMPP4ysrCx0dXXho48+gsPhUDskxhgLmqtXr6KkpAQajQbPPPMMoqKi1A4ppHAiDwNarRa7du1CVFQUbt68iS+++ELtkBhjLCiamppw4MABAMDWrVuRlZWlckShhxN5mIiPj8fu3buh1Wpx/vx5XLhwQe2QGGNsUnV3d+O9996D1WrFsmXLsHr1arVDCkmcyMNIdnY2nnzySQC0WMzNmzdVjogxxiaHxWLBe++9B5PJhNzcXDz++OPcL+4FJ/Iws2TJEqxfv35w8FtbW5vaITHGWEBJKXHgwAE0NzcjKSkJzz77LLRardphhSxO5GFo8+bNmD9/Pvr7+7Fv3z4eyc4Ym1KOHj2KqqoqGI1GPP/88zy4bQycyMOQEAI7d+5EWloa2tvb8cEHH8But6sdFmOM+e3y5cs4ffo0NBoNnn32WaSkpKgdUsjjRB6m9Ho99uzZg9jYWNTX1+P3v/89L+PKGAtryrkMAL7zne9g9uzZKkcUHjiRh7G4uDjs2bMHERERuHz5Mo4dO6Z2SIwxNiH37t3De++9B7vdjqmuZZsAABpESURBVFWrVqG4uFjtkMIGJ/Iwl56ePrj7z8mTJ3H27Fm1Q2KMsXFpb2/HO++8g/7+fhQVFeGRRx5RO6Swwol8Cpg7dy527NgBgNZkv3TpksoRMcaYb0wmE9555x309PQgLy+PtyWdAP60poglS5bg0UcfBQAcOnQIVVVVKkfEGGOj6+vrwzvvvIOOjg5kZGRg9+7d0Ol0aocVdjiRTyGrVq3Cpk2bIKXE/v37UVtbq3ZIjDHmkcViwX/8x3+gpaUFM2bMwAsvvACDwaB2WGGJE/kUs3HjRqxatQp2ux3vv/8+b33KGAs5Nptt8PyUkJCAl156ieeK+4ET+RQjhMD27duxZMmSIVe8jDEWChwOBz766CPU1tYiJiYGL7/8MuLi4tQOK6xxIp+ChBB48sknMXfuXPT19eHtt99Ga2ur2mExxqY5h8OBTz75ZHDVthdffBFJSUlqhxX2OJFPUVqtFs888wxmz56Nnp4e7N27l5M5Y0w1DocDBw4cQHl5OfR6PZ5//nmkpqaqHdaUwIl8CtPpdNizZ89gMn/rrbe4mZ0xFnQOhwMff/wxKioqYDAY8OKLLyI7O1vtsKYMTuRTXEREBPbs2YP8/Hz09vbirbfewt27d9UOizE2Tdjtduzfvx+VlZWcxCcJJ/JpQEnmhYWFMJvN2Lt3L+7cuaN2WIyxKc5ms+GDDz7A1atXYTAY8NJLLyErK0vtsKYcTuTThE6nw3PPPYeioqLBAXD19fVqh8UYm6IsFgv27duH6upqREZG4pVXXkFmZqbaYU1JnMinEZ1Oh2eeeQYLFy7EwMAA3n33Xdy8eVPtsBhjU4xyflGmmH33u99Fenq62mFNWZzIpxmtVounn34ay5Ytg9Vqxb59+1BZWal2WIyxKcJkMuG3v/0tGhoaEBcXh+9973uYNWuW2mFNabyo7TSk0Wjw5JNPwmAw4Ny5c9i/fz+6urqwdu1aCCHUDo8xFqZaW1vx7rvvoqurC8nJyXjxxReRmJiodlhTnl81ciFEkhDiiBDihvP3iCMmhHhICHHZ7adfCLHTed9bQohbbvct9Sce5jshBB555JHB7QKPHDmCw4cPw+FwqBwZYywc1dfX480330RXVxeysrLw6quvchIPEn+b1n8G4KiUshDAUee/h5BSHpNSLpVSLgWwGYAZwJduD/mJcr+U8rKf8bBxEEJgzZo12LVrF7RaLUpLS/G73/0OVqtV7dAYY2GksrISb7/9Nvr7+zFv3jy8/PLLvHZ6EPmbyHcA2Ov8ey+AnWM8fheAw1JKs5/vywJo4cKFePnll2E0GnHt2jXs3bsXZjMfIsbY6KSUOHv2LPbv3w+73Y5Vq1bhmWeeQUREhNqhTSv+JvJZUspmAHD+njnG43cDeG/YbT8XQpQLIX4lhOA97FSSk5ODV199FfHx8WhsbMSbb76J9vZ2tcNijIUoh8OBzz//HF9+SQ2s27Ztw/bt26HR8BjqYBNSytEfIMRXADwtiPvXAPZKKRPcHtshpfTYKSKESANQDiBdSml1u+0uAD2ANwDclFL+nZfnvw7gdQDIzs5eznOgJ4fJZMK+ffvQ3NyM6Oho7N69mxdwYIwNYbFYcODAAVRVVUGr1eKpp57CwoUL1Q5rShNCXJRSFnu8b6xEPsYLXwewSUrZ7EzKx6WUc7089i8ALJBSvu7l/k0AfiylfHys9y0uLpZlZWUTjpuNbmBgAB9++CFqamqg1Wrx6KOPorjY4/eHMTbNtLe34/3330dLSwuMRiN2796N3NxctcOa8kZL5P62gRwC8Irz71cAHBzlsXswrFndmfwhaM7TTgA8oTkEGAwG7NmzB6tXr4bdbsenn36KQ4cOwWazqR0aY0xFN27cwBtvvIGWlhakpKTgtdde4yQeAvytkScD+B2AbAANAJ6RUrYLIYoB/EBK+ZrzcbkAzgDIklI63J7/NYAZAASAy87n9Iz1vlwjD57y8vLBJJ6ZmYlnn30WcXFxaofFGAsiKSVOnTqFY8eOQUqJoqIiPPXUUzAYeFhTsExa07paOJEHV3NzMz744AN0dnYiJiYGzzzzDHJyctQOizEWBAMDA/jkk09QVVUFIQQeeughrF+/nhePCrLJbFpn00BaWhpef/115OXloaenB3v37kVpaSnC8SKQMea7trY2/OY3v0FVVRWMRiP27NmDDRs2cBIPMZzImU+ioqLw0ksvYc2aNXA4HPjss89w8OBBXjyGsSnq2rVr+PWvf43W1lbMmDEDf/zHf4w5c+aoHRbzgNdaZz7TaDR45JFHkJ6ejkOHDuHy5ctobGzErl27kJrqaYYiYyzcWK1WfPnll7hw4QIAYP78+dixYwf3h4cw7iNnE3Lv3j3s378fra2t0Gq12Lp1K1atWsVNboyFsXv37uGjjz5CS0sLtFottmzZgjVr1vD/6xDAg93YpLBarfjiiy+gHIvCwkLs2LEDMTExKkfGGBsPKSUuXLiAL7/8EjabDcnJydi1axfS0tLUDo05cSJnk6qqqgqHDh1CX18fYmJisHPnThQUFKgdFmPMB2azGQcPHsT169cBAA888AC2b98OvV6vcmTMHSdyNum6u7vx8ccfo66uDgCwZs0abNmyBTodD8NgLFTV1tbiwIEDMJlMMBqNeOKJJ7BgwQK1w2IecCJnQeFwOHDmzBkcO3YMDocDqamp2LlzJw+EYyzEWK1WfP311ygpKQFAmyY9/fTTiI+PVzky5g0nchZUjY2N+Oijj9DR0QGNRoN169Zhw4YNXDtnLATcunULhw4dGvz/uXHjRqxfv553LQtxnMhZ0A0MDODrr78eXDgmJSUFO3bs4J3UGFNJf38/jhw5gosXLwIAZs2ahSeffBIZGRkqR8Z8wYmcqaahoQGHDh1CW1sbhBBYuXIltmzZwgNpGAui69ev49NPP4XJZIJWq8WGDRuwbt06aLVatUNjPuJEzlRls9lw4sQJnDlzBg6HAwkJCXjiiSeQn5+vdmiMTWm9vb04fPgwKitpY8nMzEzs2LEDM2bMUDkyNl6cyFlIuHv3Lg4ePIjm5mYAwNKlS7Ft2zZERUWpHBljU4uUEhUVFfj8889hNpsRERGBLVu2YOXKldwXHqY4kbOQ4XA4cPbsWRw/fhw2mw2RkZHYtGkTVqxYwScYxgKgubkZhw8fRkNDAwBg9uzZeOKJJ5CYmKhyZMwfnMhZyGlra8Phw4dx8+ZNAMDMmTOxfft2zJ49W+XIGAtPvb29OHr0KC5dugQpJaKjo7F161YsWbKEl1idAjiRs5AkpcT169fxxRdfoKOjAwAwb948bNu2jWsPjPnIbrejtLQUJ06cQH9/PzQaDVavXo0NGzbAaDSqHR4LkNESOU/sZaoRQqCoqAgFBQUoKSnBqVOnUFVVhRs3bmDt2rVYt24dj25nbBQ3b97E4cOH0dbWBgAoKCjA9u3bkZKSonJkLJi4Rs5CRnd3N7766iuUl5cDAOLi4vDwww9j0aJF3DTImJu2tjYcOXJkcH30pKQkbN++HYWFhfx/ZYripnUWVm7fvo3Dhw+jqakJAPWfb968GXPnzuWTFJvWOjs7cfz4cXz77beQUkKv12Pjxo1YtWoVr5w4xXEiZ2FHSonLly/j+PHj6OrqAgBkZGRg8+bNmD17Nid0Nq2YTCacPHkS33zzDex2OzQaDZYtW4ZNmzYhNjZW7fBYEHAiZ2HLZrPh4sWLOHXqFHp6egDQBg9btmxBdna2ytExNrnMZjNOnz6N0tJS2Gw2CCGwaNEibNq0CUlJSWqHx4KIEzkLexaLBaWlpThz5gz6+voAAIWFhdi8eTPS0tJUjo6xwBoYGEBJSQlKSkowMDAAgGZ0PPTQQ5g5c6bK0TE1cCJnU0Z/f//gCc5isQAA5s6diwcffBBZWVnc5M7CWm9vL0pLS1FaWjp4wVpQUIDNmzcjPT1d5eiYmjiRsylneJMjAGRlZWHt2rUoKirihM7CSnt7O86ePYvLly8Pfp9zcnKwefNm5OTkqBwdCwWcyNmU5akGk5ycjLVr12LJkiU8kpeFtDt37uDMmTOoqqqCci6eO3cu1q5di+zsbL4gZYM4kbMpz2Kx4NKlSygpKUFnZycAICYmBqtWrUJxcTEiIyNVjpAxIqVETU0Nzpw5g7q6OgCAVqvF4sWLsXbtWt6ZjHnEiZxNGw6HA1evXsWZM2cGd1nT6/VYsmQJli9fjtTUVJUjZNNVf38/ysvLUVZWhpaWFgCAwWBAcXExVq9ezdPI2Kg4kbNpR0qJW7du4cyZM4MbswC0H3NxcTEWLFiAiIgIFSNk04GUEk1NTSgrK0NlZSWsVisAIDY2FmvWrMHy5cthMBhUjpKFA07kbFpraWlBWVkZysvL0d/fDwAwGo2DtXSezsMCbWBgABUVFSgrK8Pdu3cHb8/Ly0NxcTGKioqg1WpVjJCFG07kjAGwWq2orKzExYsX0djYOHh7dnY2iouLMW/ePK6lswmTUuLu3bsoKytDRUXF4PTIqKgoLF26FMuXL0dycrLKUbJwxYmcsWGUE255efngCddgMKCoqAiLFi3C7NmzodFoVI6ShYP29nZUVFSgsrISra2tg7fn5OQMXiDy7AnmL07kjHlhsVhQUVGBixcvDm7SAgDR0dGYP38+Fi1axAvNsBFMJhMqKytRWVmJO3fuDN4eFRWFxYsXY/ny5Tz6nAUUJ3LGfHD//n1UVlaioqJicH9nAIiPj8fChQuxaNEizJo1i5P6NNXX14erV6+ioqIC9fX1g/O+9Xo95s2bh4ULF2L27Nnc980mBSdyxsZB6etUalzK7msALTYzZ84czJkzB9nZ2XzSnuLa29tx48YNVFdXo66uDna7HQDN+54zZw4WLlyIOXPm8NgKNuk4kTM2QVJKNDQ0oLKyEleuXIHZbB68z2AwoKCgAHPmzEFBQQGio6NVjJQFgt1ux+3bt1FdXY0bN24M6fMWQmD27NlYuHAh5s2bB6PRqGKkbLrhRM5YADgcjsGTfHV19YiTfGZmJgoLCzFnzhxugg8jZrMZNTU1qK6uRk1NzeAURYCmKebn5/PFGlMdJ3LGJkFHR8dgze3WrVuDza4ADXrKyckZ/Jk1axaPgg8RPT09qK+vR319Perq6gZXWVOkpKQMdp9kZWVx9wkLCZzIGZtkFosFtbW1g7W67u7uIfcbjUZkZ2cjJycHubm5SEtL48QeJN3d3airqxtM3u4DGQFAp9MhOzt7MHknJSWpFClj3nEiZyyIpJTo6OgYUutTNnJR6PV6ZGZmIj09HampqUhLS0NSUhI3x/upr68Pd+/eRXNzM5qbm9HY2IiOjo4hj9Hr9cjKyhpsLcnIyOB53izkcSJnTGVdXV2DSb2+vh73798f8RiDwTCY1JWflJQUrrl70dPTM5iwlZ/hF0wAfa7u3RxpaWncXM7CzqQlciHEMwD+FsA8ACullB6zqxBiO4B/AqAF8Bsp5S+ct+cBeB9AEoBvALwkpbSM9b6cyFm4M5lMuHPnzpAkZDKZRjxOp9NhxowZSEpKQnJy8uDv5ORkREZGTvkavM1mQ0dHB+7fv4/29nbcv39/8MfT5xUREYFZs2YNuRji8QlsKpjMRD4PgAPAvwH4sadELoTQAqgGsBVAI4ALAPZIKa8KIX4H4GMp5ftCiH8F8K2U8l/Gel9O5Gwq6unpGdIs3NzcPKJZ2J3RaByS3OPi4hAbG4uYmBjExsYiKioqpBOYlBIWiwUmkwk9PT3o6emByWQaTNjt7e3o6uqCt3OUwWAYkrBTU1O5BYNNWaMlcr86hqSUVc43GO1hKwHUSClrnY99H8AOIUQVgM0Annc+bi+odj9mImdsKoqJiUFBQQEKCgoGb+vv70dbW9uIGml7ezv6+/tx586dIUuEuhNCIDo6ekhyj4mJgdFohF6vH/FjMBiG/Fuj0Yz6f1tKCSklbDYbBgYGYLFYRvy4397b2zuYtJXfyrae3mg0GiQmJg5piVD+TkhImPItEoz5IhgjPDIA3Hb7dyOAVQCSAXRKKW1ut2cEIR7GwobRaERmZiYyMzOH3C6lRG9v75Daa3d395AkaTabB2u6/hBCDP4o7638+CsiImLIRUZMTAwSExMHk3ZCQgL3ZzM2hjETuRDiKwCpHu76aynlQR/ew9Mlsxzldm9xvA7gdYC2nWRsOhNCDCY+b/8f7Hb7YCJ3T/Ceas+ebnM4HAAwZtKOiIgYUZv3VMuPiooakrBjY2Oh1+u5Vs2Yn8ZM5FLKh/18j0YAWW7/zgTQBKANQIIQQueslSu3e4vjDQBvANRH7mdMjE15Wq0W8fHxiI+Pn/BruNe+pZQjauechBlTXzBGhVwAUCiEyBNC6AHsBnBI0iX+MQC7nI97BYAvNXzGWJAIIaDRaKDVaqHT6aDVagf7zjmJMxYa/ErkQoinhBCNANYA+IMQ4gvn7elCiM8AwFnb/jMAXwCoAvA7KeUV50v8FMBfCiFqQH3mb/oTD2OMMTbd8IIwjDHGWIgbbfoZT7hkjDHGwhgncsYYYyyMcSJnjDHGwhgncsYYYyyMcSJnjDHGwhgncsYYYyyMcSJnjDHGwhgncsYYYyyMcSJnjDHGwhgncsYYYyyMcSJnjDHGwhgncsYYYyyMcSJnjDHGwhgncsYYYyyMcSJnjDHGwlhY7kcuhGgFUB/Al0wB0BbA11PTVCnLVCkHwGUJRVOlHACXJRRNRjlypJQzPN0Rlok80IQQZd42bA83U6UsU6UcAJclFE2VcgBcllAU7HJw0zpjjDEWxjiRM8YYY2GMEzl5Q+0AAmiqlGWqlAPgsoSiqVIOgMsSioJaDu4jZ4wxxsIY18gZY4yxMDZtErkQ4hkhxBUhhEMI4XU0oRBiuxDiuhCiRgjxM7fb84QQ54UQN4QQHwgh9MGJ3GOMSUKII85YjgghEj085iEhxGW3n34hxE7nfW8JIW653bc0+KXwrRzOx9ndYj3kdnu4HZOlQogS5/ewXAjxnNt9qh4Tb997t/sNzs+4xvmZ57rd91fO268LIR4JZtye+FCWvxRCXHUeg6NCiBy3+zx+19TiQ1m+K4RodYv5Nbf7XnF+H28IIV4JbuQj4hyrHL9yK0O1EKLT7b6QOSZCiH8XQrQIISq93C+EEP+fs5zlQogH3O6bvOMhpZwWPwDmAZgL4DiAYi+P0QK4CWA2AD2AbwHMd973OwC7nX//K4AfqliWXwL4mfPvnwH4hzEenwSgHUCU899vAdgVAsfEp3IA6PFye1gdEwBzABQ6/04H0AwgQe1jMtr33u0xfwrgX51/7wbwgfPv+c7HGwDkOV9Hq+Jx8KUsD7n9X/ihUpbRvmshXJbvAvhnD89NAlDr/J3o/DsxVMsx7PF/DuDfQ/SYbADwAIBKL/d/B8BhAALAagDng3E8pk2NXEpZJaW8PsbDVgKokVLWSiktAN4HsEMIIQBsBrDf+bi9AHZOXrRj2uGMwddYdgE4LKU0T2pU4zfecgwKx2MipayWUt5w/t0EoAWAxwUegszj937YY9zLtx/AFucx2AHgfSnlgJTyFoAa5+upZcyySCmPuf1fOAcgM8gx+sqX4+LNIwCOSCnbpZQdAI4A2D5JcY5lvOXYA+C9oEQ2TlLKk6BKkTc7ALwtyTkACUKINEzy8Zg2idxHGQBuu/270XlbMoBOKaVt2O1qmSWlbAYA5++ZYzx+N0b+x/i5s+nnV0IIw2QE6QNfy2EUQpQJIc4p3QMI82MihFgJqp3cdLtZrWPi7Xvv8THOz7wLdAx8eW4wjTeeV0E1KIWn75pafC3LHzm/N/uFEFnjfG4w+ByLs5sjD8DXbjeH0jEZi7eyTurx0AXqhUKBEOIrAKke7vprKeVBX17Cw21ylNsnzWhlGefrpAFYBOALt5v/CsBdUCJ5A8BPAfzdxCId8/0DUY5sKWWTEGI2gK+FEBUAuj08LpyOyTsAXpFSOpw3B+2YeArJw23DP8uQ+b8xBp/jEUK8CKAYwEa3m0d816SUNz09Pwh8KcvvAbwnpRwQQvwA1Gqy2cfnBst4YtkNYL+U0u52Wygdk7Go8v9kSiVyKeXDfr5EI4Ast39nAmgCrZmbIITQOWsjyu2TZrSyCCHuCSHSpJTNzqTQMspLPQvggJTS6vbazc4/B4QQvwXw44AE7UEgyuFshoaUslYIcRzAMgAfIQyPiRAiDsAfAPw3Z9Ob8tpBOyYeePvee3pMoxBCByAe1MToy3ODyad4hBAPgy7ANkopB5TbvXzX1EoaY5ZFSnnf7Z+/BvAPbs/dNOy5xwMeoW/G8x3ZDeBH7jeE2DEZi7eyTurx4Kb1oS4AKBQ0GloP+lIdkjRa4RiorxkAXgHgSw1/shxyxuBLLCP6m5yJRuln3gnA4wjMIBizHEKIRKWZWQiRAuBBAFfD8Zg4v1MHQH1oHw67T81j4vF7P+wx7uXbBeBr5zE4BGC3oFHteQAKAZQGKW5PxiyLEGIZgH8D8KSUssXtdo/ftaBFPpIvZUlz++eTAKqcf38BYJuzTIkAtmFoq1ww+fL9ghBiLmggWInbbaF2TMZyCMDLztHrqwF0OS/SJ/d4TOYIv1D6AfAU6KpoAMA9AF84b08H8Jnb474DoBp0xffXbrfPBp2gagB8CMCgYlmSARwFcMP5O8l5ezGA37g9LhfAHQCaYc//GkAFKFm8CyAmVMsBYK0z1m+dv18N12MC4EUAVgCX3X6WhsIx8fS9BzXtP+n82+j8jGucn/lst+f+tfN51wE8qtYxGEdZvnKeA5RjcGis71oIl+V/ALjijPkYgCK3537febxqAHwvlMvh/PffAvjFsOeF1DEBVYqanf+PG0FjLH4A4AfO+wWA/+ssZwXcZkhN5vHgld0YY4yxMMZN64wxxlgY40TOGGOMhTFO5IwxxlgY40TOGGOMhTFO5IwxxlgY40TOGPv/26sDEgAAAABB/1+3I9ATAmMiB4AxkQPAWAkS4V6ANV4CAAAAAElFTkSuQmCC\n",
            "text/plain": [
              "<Figure size 576x576 with 1 Axes>"
            ]
          },
          "metadata": {
            "tags": [],
            "needs_background": "light"
          }
        },
        {
          "output_type": "stream",
          "text": [
            "Estimate of Pi:3.088\n"
          ],
          "name": "stdout"
        }
      ]
    },
    {
      "cell_type": "code",
      "metadata": {
        "id": "Jt6PuImyxK3i",
        "colab_type": "code",
        "colab": {}
      },
      "source": [
        ""
      ],
      "execution_count": 0,
      "outputs": []
    }
  ]
 }
No results found