Created
November 20, 2024 06:42
-
-
Save ljmartin/710b0b9e970f4d2f8e0d87c0739c3427 to your computer and use it in GitHub Desktop.
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| {"cells":[{"id":"510ea8f2-4422-490b-aed6-e12031e25d94","cell_type":"code","execution_count":1,"outputs":[],"source":["import numpy as np\n","from tqdm.notebook import tqdm\n","import matplotlib.pyplot as plt\n","from scipy.integrate import odeint\n","from scipy import optimize\n"],"metadata":{}},{"id":"c04d9ec2-d923-4f41-bd99-113c8ba39a27","cell_type":"markdown","source":["# Combining Kd's\n","Tip: Skip to the end for a tldr. \n","\n","Ligand species, arising from protonation or tautomer states, will often bind with different Kd's (dissociation constant) to a target of interest. How does this affect your observed Kd in experiment? More to the point: If I predict that one protomer of a ligand is very potent, how much do I downweight that prediction when I learn that the protomer is very rare? \n","\n","There are (at least) three papers that suggest how to do this:\n","- Combining protomer energies was implemented in FEP+ in [this Schrodinger paper](https://doi.org/10.1021/acs.jctc.8b00826), equation 4. That derivation may well be correct, but the math is missing a step for me so I don't want to use it.\n","- [This paper](https://doi.org/10.1021/ct1002913), equation 22, deals with combining Kd's from multiple conformations on the _protein_ side (for a single ligand species), by summing the equilibrium binding constants for each conformation, each being weighted by the population of that conformation.\n","- Finally, [this article](https://pubmed.ncbi.nlm.nih.gov/23170882/) presents a \"master equation\" that governs the contributions of all ligand _and_ protein species (protomers, tautomers, and conformations), along with their binding modes. The derivation seems clearer to me - it's a big, messy equation but made of little, easier pieces. And it seems to match the previous derivations to my eye. So let's use this one.\n","\n","The 'master equation', equation 2, looks like this:\n","\n","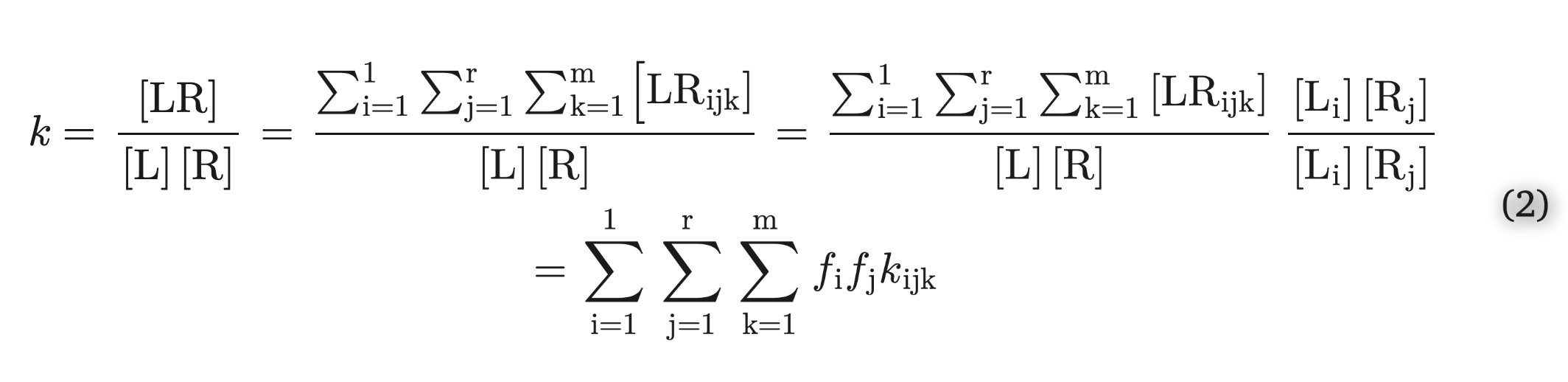\n","\n","where ijk is ligand i, receptor j, binding mode k, square brackets are concentrations, and 'f' is the fraction of unbound ligand and receptor. K is the _association_ constant, so that's 1/Kd. This equation suggests we can calculate the observed association constants 'k' by summing all the sub-k's, weighted by the fractional population in solution of that species (before binding).\n","\n","# Validation by simulation\n","We can't validate this 'master equation' theory by experiment, because it's impossible to isolate a ligand species, such as a tautomer, to measure its Kd individually and then apply the equation to compare with the observed Kd from the mixture. We only have access to that observed Kd (measured using the mixture of species). Nevertheless, more than 50 years ago [Martin and Hansch](https://pubmed.ncbi.nlm.nih.gov/5140003/) were seeing implicit experimental support for this equation when they tried incorporating the fraction of charged ligand species into their pioneering QSAR models.\n","\n","Instead of experimental observation, let's settle for a numerical simulation using ordinary differential equations! In such a simulation, we can set the on- and off-rates of every reversible reaction, and that means we can directly observe the species' concentrations as they reach equilibrium. \n","\n","To keep things manageable, this simulation will model the concentrations of a ligand with two tautomers, complexing with a single protein conformation. For the ligand, we start by equilibrating the tautomer populations to arrive at the two free fraction values (f). We can also equilibrate a mixture of the ligand tautomers and the protein to arrive at an observered Kd. Since we know all the on-rates and off-rates, we can calculte association constants (k) for each species individually. Then we can predict the observed Kd using the master equation (the 'f's and the 'k's), and see if the values match up. \n","\n","In a little more detail:\n","- Using an ODE, we can simulate the % of free ligand, free protein, and bound complex that is implied by a reversible reaction `P+L<->PL`\n","- Likewise, we can simulate the % of tautomer species in the same way, where the reversible reaction is `L1<->L2`\n","- Likewise, we can simulate the % of each unbound and bound tautomer species to a protein, `P+L1+L2<->PL1+L2<->PL1+PL2<->PL2+L1`. In practice we only care about `PL1+PL2`, because that's what is measurable in a real experiment, i.e. it represents the combined, observed, Kd\n","- To set up these simulations, we have to input an on-rate and an off-rate for each process. Since the equilibrium binding constant is just on-rate/off-rate, we know the individual Kd's of each ligand species in this simulation, so we know exactly how to generate a combined Kd using the master equation.\n","- After the simulation of the protein and the ligand species mixture, we can then fit a kinetic model to the signal from the combined `PL1+PL2`, as you might do in an experiment, to generate the \"experimental\" apparent Kd. \n","- Finally, we can compare the apparent Kd (from our simulated 'experimental' data) to the predicted combined Kd (from the master equation) and see if the two match up. "],"metadata":{},"attachments":{}},{"id":"35a5b2bd-bae1-4763-936d-cab578f1befd","cell_type":"markdown","source":["# Start with the tautomers\n","To make the master equation work, we'd need the tautomer transition reaction to happen much faster than the protein complexation process. For many tautomers of interest, this is a plausible assumption (see the paper). In this case, I set the forward and reverse-rates of the tautomer transition to lead to ~95% tautomer 1, and ~5% tautomer 2, while both being pretty fast. \n","\n","The cell below generates an equilibrated solution of the tautomers by starting from an equal mixture (impossible to realise in practice) and then waiting 2 seconds. You can see that the rates are reasonably fast because the equilibration happens in <1s. "],"metadata":{},"attachments":{}},{"id":"80117db7-70db-48a5-8b0c-67435493f39d","cell_type":"code","execution_count":2,"outputs":[{"output_type":"display_data","data":{"text/plain":["<Figure size 640x480 with 1 Axes>"],"image/png":["iVBORw0KGgoAAAANSUhEUgAAAioAAAHACAYAAACMB0PKAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjkuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy80BEi2AAAACXBIWXMAAA9hAAAPYQGoP6dpAABOKElEQVR4nO3dd3wUdf4/8NdsSTY9gXQIIfQWIEgROASRjihX8ChyoMJ5Hko7FfieEMBDwQM7CuIJ+JPmHUWUorTQpPdIhxCQEEIgyaZnszu/Pza7siSEbMvMTl7Px2Mfuzs7O/t+ZxL2xWeaIIqiCCIiIiIZUkldABEREdHDMKgQERGRbDGoEBERkWwxqBAREZFsMagQERGRbDGoEBERkWwxqBAREZFsMagQERGRbDGoEBERkWwxqBAREZFsKSao7NmzB4MGDUJ0dDQEQcCGDRvc/pk3b97E888/j9q1a8PHxwfx8fE4evSo2z+XiIioplBMUMnPz0ebNm2wcOHCavm8rKwsdO3aFVqtFlu2bMHZs2exYMEChISEVMvnExER1QSCEi9KKAgC1q9fj8GDB1unFRcX45///CdWrVqF7OxstGrVCvPmzUOPHj0c+oypU6di//792Lt3r2uKJiIionIUM6LyKK+++ioOHDiA1atX4/Tp0xgyZAj69euHS5cuObS8jRs3on379hgyZAjCw8ORkJCAJUuWuLhqIiKimq1GjKhcv34dDRo0wPXr1xEdHW2dr1evXujYsSPeeecduz9Dp9MBACZPnowhQ4bgyJEjmDBhAhYtWoRRo0a5pA8iIqKaTiN1AdXhzJkzMBqNaNKkic304uJi1K5dGwBw/vx5NG/evNLlTJkyBXPnzgUAmEwmtG/f3hpyEhISkJyczKBCRETkQjUiqOTl5UGtVuPYsWNQq9U2r/n7+wMAGjRogHPnzlW6HEuoAYCoqCi0aNHC5vXmzZtj7dq1LqqaiIiIakRQSUhIgNFoREZGBrp161bhPF5eXmjWrFmVl9m1a1dcuHDBZtrFixcRGxvrVK1ERET0G8UElby8PFy+fNn6PCUlBSdPnkStWrXQpEkTjBgxAn/5y1+wYMECJCQk4M6dO9ixYwdat26NgQMH2v15kyZNQpcuXfDOO+/gueeew+HDh/HFF1/giy++cGVbRERENZpidqZNSkrCk08+WW76qFGjsGzZMhgMBvzrX//C119/jZs3byI0NBSPP/44Zs2ahfj4eIc+84cffsC0adNw6dIlxMXFYfLkyRg7dqyzrRAREVEZxQQVIiIiUp4acx4VIiIi8jwMKkRERCRbHr0zrclkQlpaGgICAiAIgtTlEBERURWIoojc3FxER0dDpap8zMSjg0paWhpiYmKkLoOIiIgccOPGDdStW7fSeTw6qAQEBAAwNxoYGOjSZRsMBvz000/o06cPtFqtS5ctB+zP8ym9R6X3Byi/R/bn+dzVo16vR0xMjPV7vDIeHVQsm3sCAwPdElR8fX0RGBioyF9A9uf5lN6j0vsDlN8j+/N87u6xKrttcGdaIiIiki0GFSIiIpItBhUiIiKSLQYVIiIiki0GFSIiIpItBhUiIiKSLQYVIiIiki0GFSIiIpItBhUiIiKSLQYVIiIiki0GFSIiIpItBhUiIiKSLY++KCFRTSOKYtk9YDSJMIpAqdEEqEwQRUDEb6/b3EO877F5OSLum+eB94r3fVal9Tyy3ke9/+EzlBpKkVMCZOQWQ6sxSlJDVd5flRoeptRgwL1iIC27EBptqYNLcY9HXyru0UpLS5FVDNzKKYJG497+qnBtO5czGEqRXdaf1s71J7jkJ+x+hlID8g3S1sCgQoogiiJKjCYUlZhQaDAit7AIN/OBEzeyUWoSUGgwoshgfq3QYESxwYgSowmlRhEGowmGsvtSowklRhGlRpPNdIPRhFKTiJJS871JFGEyiTCVBQaTaLkBJpMIo+W5CTCJYtk8sM5nNIn3hQ3RGhQqDRMV0mDywe3u/wFLRoMZx3ZLXYSbaTDr+F6pi3AjDWYe3yN1EW6kQaKi+wPa1VZhiISfz6BCslJkMOJufgnu5hXjbn4J7uWV4G5+MbILDMgtKkVukeW+FPqi36blFZfCVO7LXAOcPixFG1QFlf0P2PKSKIoVXga+skvDP+r/qZV/7iPeXYWa7WUyGqFSqx18t3s4OkJUkWrpz5UF2/WxIkwmE1QqlV0jJI8axZMblcSDPwwqVG1KjSb8mlWIG1kFSMsuxM2sQtzMLkJadiHScgpxJ7cYBSUPH+KvKrVKgE6rgspUiiB/X/h6qeGjVUNXdvPRquGtVcFLrYJGrYKXWoBGrYL2gcdatVB2r4JGLZTNL0CjEqASBKjL7lUqASoBUAsChLLpapX5y1QtWObBfe8xP7Y8F8qeA+YvUcs/eObHsH4DChB+mwbzsPqO7dvRu3dvaLUa8/uE376IBZhrsMz/4LJt7h9YtuV9jxpOrywwOMtgMGDz5s0YMGAAtFqt2z5HSr/12FeRPbI/z2fpUUoMKuRyRpOIyxl5+CUtB1fu5OFKRj6u3MlD6t0ClBhNj3y/Vi2gtp83avl5oba/F2r7eSHY1wsBOk3ZTWtzH6jTwN9bC19vcwjRqlX3/QPSTcH/gKjgpwWCfbWK7ZGIiEGFnJaRW4SDV+/hxPUsnPk1B7+k6VFoqHhkxFujQkwtX9QJ9kGdEB/UCfZBdLAO0UE+iAjUoZa/FwK8NW79nzoREXkOBhWym77IgP2XMvHzlbs4cPUuLmfklZvHz0uNltFBaBzhj4Zh/mgQ5oeGYf6oE+wDldQbPImIyGMwqFCV3MwuxPazt7H93G0cvHoXBuNvO4MJAtAiKhAd6tdC67pBaF03CHGh/lAzkBARkZMYVOih7uQWY+OpNHx38iZO/5pj81rDMD90axyGzg1ro1NcLQT7eklUJRERKRmDCtkoMhjx09nbWH/8V+y5lAlj2TG/KgF4LDYEvVtEoHeLSMSF+klcKRER1QQMKgQA+DWrACsOXceaIzdwL7/EOr1NTDD+kFAHA1tHIdTfW8IKiYioJmJQqeGOpmbhq5+vY8e529YTpkUH6fDHx+picEIdNAzzl7ZAIiKq0RhUaqiSUhN23BTw/cEj1tOz/65RKEZ2jsVTzcKhUfN6lUREJD0GlRpo98U7mLEhGan3zKe17tMiAm/2a4ZG4Rw9ISIieWFQqUEycovwrx/OYeOpNABAgFbElAEtMbxTfZ7bhIiIZIlBpYbYcOImZnyXDH1RKVQC8JfH66G58Sr+0L4uQwoREckWg4rC5RYZkPjdL1h34iYAoFWdQLz7+9ZoFuGLzZuvSlwdERFR5RhUFOxCei7++v+OIvVuAVQCMP6pxnj1yUbQlF20j4iISO4YVBTqp1/SMWnNSeSXGFEn2AcfDm2LDvVrSV0WERGRXRhUFEYURSzafRXv/Xgeogh0blAbn41ohxA/nuKeiIg8D4OKgoiiiDmbzuHLfSkAgL90jsX0p1tAy3OiEBGRh2JQUQijScS0dafx7dFfAQDTn26Bl34XJ3FVREREzmFQUQCjScTkb0/iu5NpUAnAvD+2xpD2MVKXRURE5DQGFQ8niiL+uf4MvjuZBo1KwKfDE9CvVZTUZREREbkEd17wYKIoYvYPZ7H6yA2oBOCjoQwpRESkLAwqHmzR7qtYuv8aAOC9P7XBwNYMKUREpCwMKh5qa3I65m09DwBIHNQCf3qsrsQVERERuR6DigdKvpmDSWtOAgBGdY7FC115dA8RESkTg4qHycwrxpjlR1FoMOKJJmGY/nQLqUsiIiJyGwYVD2IyiZi05iTS9UVoGOaHT4cnQMOTuRERkYLxW86DfL77CvZeyoROq8Lnzz+GQJ1W6pKIiIjcikHFQxxLvYcFP10AAMx+thWaRARIXBEREZH7Mah4gCKDEW/89zRMIjC4bTSG8AgfIiKqIRhUPMCCny7gamY+IgK9MeuZVhAEQeqSiIiIqgWDiswdS71nvRryu3+IR5Av90shIqKag0FFxopLjXjjf6chisAf29VFz2YRUpdERERUrRhUZOzLvSm4eicfYQHemMHzpRARUQ3EoCJTadmF+HTnZQDAPwc05yYfIiKqkRhUZGrO5nMoNBjRoX4Inm0bLXU5REREkmBQkaGfr2Ri0+lbUAnAzGda8igfIiKqsRhUZMZkEjH7+7MAgOcfj0XL6CCJKyIiIpIOg4rMbDyVhvPpuQjQaTCpVxOpyyEiIpIUg4qMlJSasGCb+TT5f+veECF+XhJXREREJC0GFRlZfeQ6btwrRFiAN17oWl/qcoiIiCTHoCITRQYjPt5hPhx5/FON4eulkbgiIiIi6TGoyMTqw9eRmVeMuiE+GNohRupyiIiIZIFBRQZKSk34Ys9VAOZ9U7RqrhYiIiKAQUUWNpy8ibScIoQFeONPj9WVuhwiIiLZYFCRmNEk4vOkKwCAsd3ioNOqJa6IiIhIPhhUJLbtbDpSMvMR5KPFiE6xUpdDREQkKwwqElu6/xoAYESnevDz5pE+RERE92NQkdDZND0OpdyDWiVgZGeOphARET2IQUVCy3++BgDo1yoSUUE+0hZDREQkQwwqErmXX4INJ28CAF7oUl/aYoiIiGRK0qBiNBoxffp0xMXFwcfHBw0bNsTbb78NURSlLKtafHv0BopLTWhVJxCPxYZIXQ4REZEsSbr35rx58/D5559j+fLlaNmyJY4ePYoXXngBQUFBGD9+vJSluZUoivj2yA0AwMjHYyEIgsQVERERyZOkQeXnn3/Gs88+i4EDBwIA6tevj1WrVuHw4cNSluV2R1OzcDUzH75eagxsHS11OURERLIl6aafLl26YMeOHbh48SIA4NSpU9i3bx/69+8vZVlut6ZsNOXp1lHw5yHJREREDyXpt+TUqVOh1+vRrFkzqNVqGI1GzJkzByNGjKhw/uLiYhQXF1uf6/V6AIDBYIDBYHBpbZbluXq5ecWl2HQ6DQDwh7ZRLl9+VbmrP7lQen+A8ntUen+A8ntkf57PXT3aszxBlHDP1dWrV+ONN97Av//9b7Rs2RInT57ExIkT8f7772PUqFHl5p85cyZmzZpVbvrKlSvh6+tbHSU77cBtAauvqhGuE/F/bY3g7ilERFTTFBQUYPjw4cjJyUFgYGCl80oaVGJiYjB16lSMGzfOOu1f//oXvvnmG5w/f77c/BWNqMTExCAzM/ORjdrLYDBg27Zt6N27N7RarcuWO3TJYRy7no03+zbG2N/FuWy59nJXf3Kh9P4A5feo9P4A5ffI/jyfu3rU6/UIDQ2tUlCRdNNPQUEBVCrb3WTUajVMJlOF83t7e8Pb27vcdK1W67ZfElcu+9esAhy7ng1BAP74WD1Z/GK782cnB0rvD1B+j0rvD1B+j+zP87m6R3uWJWlQGTRoEObMmYN69eqhZcuWOHHiBN5//328+OKLUpblNt+fugUA6BRXCxGBOomrISIikj9Jg8onn3yC6dOn4+9//zsyMjIQHR2Nl19+GTNmzJCyLLfZeMq8E+0zbepIXAkREZFnkDSoBAQE4MMPP8SHH34oZRnV4nJGLs7d0kOjEtC/VaTU5RAREXkEXuunmmws2+zzRJMwhPh5SVwNERGRZ2BQqQaiKOJ762YfnomWiIioqhhUqsGF27lIycyHl0aFXi0ipC6HiIjIYzCoVIOffrkNAHiicShPmU9ERGQHBpVq8NPZdABAnxbciZaIiMgeDCpudjO7EMk39VAJwFPNw6Uuh4iIyKMwqLjZtl/MoyntY2uhtn/5s+oSERHRwzGouNlPZ837p/RpyZ1oiYiI7MWg4kY5BQYcSrkHAOjNo32IiIjsxqDiRkkXM2A0iWgaEYDY2n5Sl0NERORxGFTcaPfFOwCAJ5txJ1oiIiJHMKi4ickkYs/FTABA9yZhEldDRETkmRhU3OTsLT0y84rh56XGY7EhUpdDRETkkRhU3MSy2adzw1B4afhjJiIicgS/Qd3EElS6N+VmHyIiIkcxqLiBvsiA46lZAIDujRlUiIiIHMWg4gY/X76LUpOIBqF+qFfbV+pyiIiIPBaDihvsvWTe7PMEj/YhIiJyCoOKGxy4ehcA0KVhbYkrISIi8mwMKi52W1+Eq3fyIQhApzgGFSIiImcwqLjYwbLRlBZRgQjy1UpcDRERkWdjUHExS1Dp3ICjKURERM5iUHGxA1fKggr3TyEiInIag4oL3copxLW7BVAJQIe4WlKXQ0RE5PEYVFzIMpoSXycIgTrun0JEROQsBhUXsuyf8jg3+xAREbkEg4oLHUq5BwB4nDvSEhERuQSDiovcyS1G6t0CCALQrl6I1OUQEREpAoOKixy/br4IYZPwAAT5cP8UIiIiV2BQcRHL1ZIfq8/RFCIiIldhUHGRo5agws0+RERELsOg4gLFpUac+TUHAPBYLIMKERGRqzCouEDyTT1KjCbU9vNCbG1fqcshIiJSDAYVFziWaj4s+bHYEAiCIHE1REREysGg4gLHLPuncLMPERGRSzGoOEkURRxLzQbAoEJERORqDCpO+jWrEJl5xdCqBbSqEyR1OURERIrCoOKk02VH+zSLDIROq5a4GiIiImVhUHHS6ZvZAIDWdTmaQkRE5GoMKk46fcM8osKgQkRE5HoMKk4wmUQk37QElWBpiyEiIlIgBhUnpNzNR25xKXRaFRqH+0tdDhERkeIwqDjBctr8ltFB0Kj5oyQiInI1frs64dSv2QCAeB6WTERE5BYMKk6wjKi0iWFQISIicgcGFQeVGk1ITjMHlfg6wdIWQ0REpFAMKg66fCcPRQYT/L01aBDqJ3U5REREisSg4qDfdqQNhErFKyYTERG5A4OKg87dygUAtIgOlLgSIiIi5WJQcdC5W3oAQIsoBhUiIiJ3YVBxgCiKOFsWVJozqBAREbkNg4oDbuUUIafQAI1KQOMInpGWiIjIXRhUHGDZ7NMwzB/eGrXE1RARESkXg4oDzqZZNvsESFwJERGRsjGoOOBcetmOtDzih4iIyK0YVBxgOTSZO9ISERG5F4OKnfKLS3Htbj4ABhUiIiJ3Y1Cx0/n0XIgiEBbgjVB/b6nLISIiUjQGFTud4/lTiIiIqg2Dip3Op/OIHyIiourCoGKni7fzAABNIxhUiIiI3I1BxQ6iKOLSbfMRP00YVIiIiNyOQcUOd/NLkFVggCCYz0pLRERE7iV5ULl58yaef/551K5dGz4+PoiPj8fRo0elLqtCF8tGU2JCfOHjxVPnExERuZtGyg/PyspC165d8eSTT2LLli0ICwvDpUuXEBISImVZD3U5w7x/ShNeiJCIiKhaSBpU5s2bh5iYGCxdutQ6LS4uTsKKKmcZUWkUzv1TiIiIqoOkm342btyI9u3bY8iQIQgPD0dCQgKWLFkiZUmVunSbIypERETVSdIRlatXr+Lzzz/H5MmT8X//9384cuQIxo8fDy8vL4waNarc/MXFxSguLrY+1+vN5zQxGAwwGAwurc2yvPuXaxlRiavl4/LPq24V9ackSu8PUH6PSu8PUH6P7M/zuatHe5YniKIouvTT7eDl5YX27dvj559/tk4bP348jhw5ggMHDpSbf+bMmZg1a1a56StXroSvr69ba80zAP88qoEAEe91NIL70hIRETmmoKAAw4cPR05ODgIDKz/Tu6QjKlFRUWjRooXNtObNm2Pt2rUVzj9t2jRMnjzZ+lyv1yMmJgZ9+vR5ZKP2MhgM2LZtG3r37g2tVotDKfeAo0dRN8QXgwd1c+lnSeHB/pRG6f0Byu9R6f0Byu+R/Xk+d/Vo2SJSFZIGla5du+LChQs20y5evIjY2NgK5/f29oa3d/kLAWq1Wrf9kliWffVuIQDzid6U9Avpzp+dHCi9P0D5PSq9P0D5PbI/z+fqHu1ZlqQ7006aNAkHDx7EO++8g8uXL2PlypX44osvMG7cOCnLqpBlR9rGPCMtERFRtZE0qHTo0AHr16/HqlWr0KpVK7z99tv48MMPMWLECCnLqpBlR9rG4Tzih4iIqLo4vemnuLi4ws0xVfX000/j6aefdrYMt7tyJx8A0IhBhYiIqNrYPaKyZcsWjBo1Cg0aNIBWq4Wvry8CAwPRvXt3zJkzB2lpae6oU1L6IgMy88yHRTcI85O4GiIiopqjykFl/fr1aNKkCV588UVoNBpMmTIF69atw48//ogvv/wS3bt3x/bt29GgQQP87W9/w507d9xZd7W6lmkeTQkL8EaATtk7TBEREclJlTf9vPfee/jggw/Qv39/qFTl881zzz0HwHyRwU8++QTffPMNJk2a5LpKJXS1bLNPXChHU4iIiKpTlYNKRSdgq0idOnUwd+5chwuSo6tlIyoNGFSIiIiqlaRH/XiKq3fMhyZz/xQiIqLqZddRP7Nnz67SfDNmzHCoGLlKybRs+uERP0RERNXJrqAyc+ZMREdHIzw8HA+7RJAgCIoKKqIo3hdUOKJCRERUnewKKv3798fOnTvRvn17vPjii3j66acr3LFWSW7nFqOgxAi1SkC9Wu698CERkRKZTCYUFRVJXYbLGQwGaDQaFBUVwWg0Sl2OWzjao1arhVrtmqv32hVUNm3ahLS0NCxfvhxvvPEGXn75ZfzlL3/Biy++iKZNm7qkILm5llkAAIgJ8YGXRtmhjIjI1dRqNVJSUh46Cu/JRFFEZGQkbty4AUEQpC7HLZzpMTg4GJGRkU7/bOw+M210dDSmTZuGadOmYc+ePVi6dCk6dOiA+Ph4bN++HT4+Pk4VJDcpd7nZh4jIEaIoIigoCGq1GnXq1FHcCLzJZEJeXh78/f0V15uFIz2KooiCggJkZGQAAKKiopyqwalT6Hfo0AHXrl3D2bNnceLECRgMBuUFlbIRFe5IS0RkH6PRCB8fH4SFhcHXV3mbzk0mE0pKSqDT6RQdVBzp0ZIFMjIyEB4e7tRmIId+sgcOHMDYsWMRGRmJTz75BKNGjUJaWhoCAwMdLkSuLDvS8tBkIiL7GI1GCIIArZZn9K6JLOHUYDA4tRy7RlTee+89LFu2DJmZmRgxYgT27t2L1q1bO1WA3FlGVHiyNyIi+1j2S1Hq/htUOVetd7uCytSpU1GvXj0899xzEAQBy5Ytq3C+999/3xW1Sa7UBPyaXQgAiOOIChERUbWzK6g88cQTEAQBv/zyy0PnUVJyvlcMGE0idFoVIgN1UpdDRERu9qjvsMTERMycOdPh5V+7dg1xcXE4ceIE2rZt6/BypPDFF19g5cqVOH78OHJzc5GVlYXg4GC3f65dQSUpKclNZcjT3SLzL2y9Wr6KCmBERFSxW7duWR+vWbMGM2bMwIULF6zT/P2Vf2CFwWCocL+igoIC9OvXD/369cO0adOqrR5l7qbsIpnF5vt6tbjZh4ioJoiMjLTegoKCIAiC9Xl+fj5GjBiBiIgI+Pv7o1OnTuX+Ay8IAjZs2GAzLTg42LqrRFxcHAAgISEBgiCgR48eAMxH18yePRt169aFt7c32rZti61bt1qXce3aNQiCgG+//RbdunWDj48POnTogIsXL+LIkSNo3749/P390b9/f9y5c8fm87/88ks0b94cOp0OzZo1w2effVZuuWvWrEH37t2h0+mwYsWKCn82EydOxNSpU/H444878JN1XJWDyty5c1FQUFCleQ8dOoRNmzY5XJRcZN43okJERDVbXl4eBgwYgB07duDEiRPo27cvhg0bhuvXr1d5GYcPHwYAbN++Hbdu3cK6desAAB999BEWLFiA+fPn4/Tp0+jbty+eeeYZXLp0yeb9iYmJeOutt3D8+HFoNBoMHz4cb775Jj766CPs3bsXly9ftrmMzYoVKzBjxgzMmTMH586dwzvvvIPp06dj+fLlNsudOnUqJkyYgHPnzqFv376O/ojcosqbfs6ePYvY2FgMGTIEgwYNQvv27REWFgYAKC0txdmzZ7Fv3z588803SEtLw9dff+22oqvL3bIzPsfWZlAhInKWKIooNEhzqnkfrdrpTfht2rRBmzZtrM9nz56NtWvX4vvvv8drr71WpWVYvjdr166NyMhI6/T58+djypQpGDp0KABg3rx52LVrFz788EMsXLjQOt/rr79uDRITJkzAsGHDsGPHDnTt2hUA8NJLL9kc6JKYmIgFCxbgD3/4AwDziM7Zs2exePFijBo1yjrfxIkTrfPITZWDytdff41Tp07h008/xfDhw6HX66FWq+Ht7W0daUlISMCYMWMwevRo6HSev/NpZjFHVIiIXKXQYESLGT9K8tlnZ/eFr5dT5zhFXl4eZs6ciU2bNuHWrVsoLS1FYWGhXSMqFdHr9UhLS7OGDYuuXbvi1KlTNtPuPyVIREQEACA+Pt5mmuWMsPn5+bhy5QpeeukljB071jpPaWkpgoKCbJbbvn17p3pwJ7vWWps2bbBkyRIsXrwYp0+fRmpqKgoLCxEaGoq2bdsiNDTUXXVWO1EUrSMq9TiiQkRU473++uvYtm0b5s+fj0aNGsHb2xt//OMfUVJSYp1HEIRy1zVy9oRn97t/J1fLCNGD00wmEwBzsAKAJUuWoFOnTjbLefBMsX5+8t0X06F4qVKp0LZtW487tMoe9/JLUGISIAhA3RBlXRaAiEgKPlo1zs6WZv8HH63zV/Ldv38/Ro8ejd///vcAzCMhD46mhIWF2Rw5dOnSJZv9O728vADA5krEgYGBiI6Oxv79+9G9e3ebz+vYsaPD9UZERCA6OhpXr17FiBEjHF6O1JwbB1Ow6/fMJ3qLDNTBW+OaS1UTEdVkgiA4vflFSo0bN8a6deswaNAgCIKAt956q9zoSc+ePfHpp5+ic+fOMBqNmDJlis2IR3h4OHx8fLB161bUrVsXOp0OQUFBeOONN5CYmIiGDRuibdu2WLp0KU6ePPnQI3CqatasWRg/fjyCgoLQr18/FBcX4+jRo8jKysLkyZPtWlZ6ejrS09Nx+fJlAMCZM2cQEBCAevXqoVatWk7VWRkenvwQ17PMQaVeLY6mEBGR+azrISEh6NKlCwYNGoS+ffuWu4zMggULEBMTg27dumH48OF4/fXXbS7IqNFo8PHHH2Px4sWIjo7Gs88+CwAYP348Jk+ejH/84x+Ij4/H1q1bsXHjRjRu3NipmseMGYMvv/wSS5cuRXx8PLp3745ly5ZZD5O2x6JFi5CQkGDd3+WJJ55AQkICNm7c6FSNjyKID8ZBD6LX6xEUFIScnByXXxDx/Z/O4+OdV/CndnUw/7m2Ll22HBgMBmzevBkDBgxQ5AXDlN4foPweld4foPwec3NzcfHiRTRv3lyxV0/W6/UIDAxU9NWTHe2xqKgIKSkpiIuLK3eAjT3f38r8ybrADY6oEBERSY5B5SFu3DPv/BTDHWmJiIgk49Kg8tlnn2H27NmuXKRkbtyzjKgob7iSiIjIU7g0qKxdu9bmjHieqshgxO1c84V+Yrjph4iISDIuPU5sx44drlycZG7czUME7iFAbUCwj/J2cCMiIvIUnntAuxsZj3yFQ7qZ2It2EISRUpdDRERUYzm06efdd9/FV199VW76V199hXnz5jldlNTuekUBAOoJGRJXQkREVLM5FFQWL16MZs2alZvesmVLLFq0yOmipNa1fQcAQB1kAJ57mhkiIiKP51BQSU9PR1RUVLnpD17jwGMFxUAUVNCIJUA+R1WIiIik4lBQiYmJwf79+8tN379/P6Kjo50uSnIaLyCwDgBAyLombS1EREQ1mENBZezYsZg4cSKWLl2K1NRUpKam4quvvsKkSZOs1wDwdGJIffOD7FRJ6yAiouojCEKlt5kzZzq1/GvXrkEQBJw8edIl9VaXe/fu4bXXXkPTpk3h4+ODevXqYfz48cjJyXH7Zzt01M8bb7yBu3fv4u9//ztKSkoAADqdDlOmTMG0adNcWqBkgmMB7IWQlSJ1JUREVE3u331hzZo1mDFjBi5cuGCd5u/vL0VZ1cpgMJS79lRaWhrS0tIwf/58tGjRAqmpqfjb3/6GtLQ0/O9//3NrPQ6NqAiCgHnz5uHOnTs4ePAgTp06hXv37mHGjBmurk8yYoj5ypICR1SIiGqMyMhI6y0oKAiCIFif5+fnY8SIEYiIiIC/vz86deqEpKQkm/cLgoANGzbYTAsODraeDNVy1eKEhAQIgoAePXoAMF/8b/bs2ahbty68vb3Rtm1bbN261boMy0jMt99+i27dusHHxwcdOnTAxYsXceTIEbRv3x7+/v7o378/7ty5Y/P5X375JZo3bw6dTodmzZrhs88+K7fcNWvWoHv37tDpdFixYkW5n0urVq2wdu1aDBo0CA0bNkTPnj0xZ84cfP/99ygtLXXwp101Tp2Z1t/fHx06dECrVq3g7e3tqppkQQyONT/gPipERAQgLy8PAwYMwI4dO3DixAn07dsXw4YNw/Xr16u8jMOHDwMAtm/fjlu3bmHdunUAgI8++ggLFizA/Pnzcfr0afTt2xfPPPMMLl26ZPP+xMREvPXWWzh+/Dg0Gg2GDx+ON998Ex999BH27t2Ly5cv2wwarFixAjNmzMCcOXNw7tw5vPPOO5g+fTqWL19us9ypU6diwoQJOHfuHPr27VulXixXPtZo3HtKNoeWnp+fj7lz52LHjh3IyMiAyWSyef3q1asuKU5SZUGFO9MSEbmIKAKGAmk+W+sLCIJTi2jTpg3atGljfT579mysXbsW33//PV577bUqLSMsLAwAULt2bURGRlqnz58/H1OmTMHQoUMBAPPmzcOuXbvw4YcfYuHChdb5Xn/9dWuQmDBhAoYNG4YdO3aga9euAICXXnrJ5lI2iYmJWLBgAf7whz8AMI/onD17FosXL8aoUaOs802cONE6T1VkZmbi7bffxl//+tcqv8dRDgWVMWPGYPfu3Rg5ciSioqIgOLny5ci66Sc/AyjJB7z8JK6IiMjDGQqAdyQ6MvT/0pz+dzwvLw8zZ87Epk2bcOvWLZSWlqKwsNCuEZWK6PV6pKWlWcOGRdeuXXHq1Cmbaa1bt7Y+joiIAADEx8fbTMvIMJ9WIz8/H1euXMFLL71kc6BLaWkpgoKCbJbbvn17u+odOHAgWrRo4fTOxVXhUFDZsmULNm3aVO6Hqig+wShR+8LLWABkpQIRLaSuiIiIJPT6669j27ZtmD9/Pho1agRvb2/88Y9/tB5UApj3UREfOFGowWBwWQ337+RqGSR4cJplK0deXh4AYMmSJejUqZPNctRqtc1zP7+qhbjc3Fz069cPAQEBWL9+fbmdbt3BoaASEhKCWrVquboW2SnwCodX4TUgK4VBhYjIWVpf88iGVJ/tpP3792P06NH4/e9/D8A8svDgaMqDJz69dOkSCgp+29zl5eUFADAajdZpgYGBiI6Oxv79+9G9e3ebz+vYsaPD9UZERCA6OhpXr17FiBEjHF6OhV6vR9++feHt7Y2NGzdCp9M5vcyqcCiovP3225gxYwaWL18OX1/nV75c5XuHI7jwGneoJSJyBUHw6M3ojRs3xrp16zBo0CAIgoC33nqr3OhJz5498emnn6Jz584wGo2YMmWKzahDeHg4fHx8sHXrVtStWxc6nQ5BQUF44403kJiYiIYNG6Jt27ZYunQpTp48WeEROPaYNWsWxo8fj6CgIPTr1w/FxcU4evQosrKyMHny5CovR6/Xo1+/figoKMA333wDvV4PvV4PwBzOHhyhcSWHgsqCBQtw5coVREREoH79+uWGfo4fP+6S4qSW7x1ufnCP51IhIqrp3n//fbz44ovo0qULQkND8eabbyIrK8tmngULFuCFF15At27dEB0djY8++gjHjh2zvq7RaPDxxx9j9uzZmDFjBrp164akpCTrydP+8Y9/ICMjAy1atMDGjRvRuHFjp2oeM2YMfH198e9//xtvvPEG/Pz8EB8fj4kTJ9q1nOPHj+PQoUMAgEaNGtm8lpKSgvr16ztVZ2UcCiqDBw92cRnyVOBl3jsbPOkbEVGNM3r0aIwePdr6vH79+ti5c6f1uclkwvPPP4/AwEDrtOjoaPz44482y8nOzrZ5PmbMGIwZM8ZmmkqlQmJiIhITEyuspX79+uVGb3r06FFu2oM1A8Dw4cMxfPjwKi+3IhV9VnVxKKg87AepNPne5j2quemHiIhIGk6dpeXYsWM4d+4cAKBly5ZISEhwSVFykW8dUUkFTEZA5b5tcERERFSeQ0ElIyMDQ4cORVJSEoKDgwGYh7aefPJJrF692npCG09X6FUbotoLgrEEyL4O1IqTuiQiIqIaxaFT6L/22mvIzc3FL7/8gnv37uHevXtITk6GXq/H+PHjXV2jdAQVUHbiN9y9Im0tRERENZBDQWXr1q347LPP0Lx5c+u0Fi1aYOHChdiyZYvLipMDsXbZ3s13L0tbCBERUQ3kUFAxmUwVno1Oq9WWu+6PpxNrNTQ/uHup8hmJiMiG5cypUh0tQtJy1Xp3KKj07NkTEyZMQFrab2cYvHnzJiZNmoSnnnrKJYXJBUdUiIgco1arIYqiS08hT57DckZeZ0+z79DOtJ9++imeeeYZ1K9fHzExMQCAGzduoFWrVvjmm2+cKkh2rCMq3EeFiMgearUahYWFuHPnDry8vKBSOfR/Y9kymUwoKSlBUVGR4nqzcKRHURRRUFCAjIwMBAcHO33WWoeCSkxMDI4fP47t27fj/PnzAIDmzZujV69eThUjR9ZNPzk3gJICwEu5lwwgInIlQRCQnZ2NsLAwpKamSl2Oy4miiMLCQvj4+Fg3cymNMz0GBwcjMjLS6RocPo+KIAjo3bs3evfu7XQRsuZbG9AFA0XZwL2rQGQrqSsiIvIYJpMJcXFxitxPxWAwYM+ePXjiiSeq5SrCUnC0R61W67Lr/9gVVHbu3IlXX30VBw8etDllMADk5OSgS5cuWLRoEbp16+aS4mRBEIDajYCbR837qTCoEBHZRaVSKfKLXK1Wo7S0FDqdTpH9AfLo0a6Nah9++CHGjh1bLqQAQFBQEF5++WW8//77LitONrhDLRERkSTsCiqnTp1Cv379Hvp6nz59bK4SqRihDCpERERSsCuo3L59u9KhH41Ggzt37jhdlOxwRIWIiEgSdgWVOnXqIDk5+aGvnz59GlFRUU4XJTu1G5vvGVSIiIiqlV1BZcCAAZg+fTqKiorKvVZYWIjExEQ8/fTTLitONmo1MN8XZgH5d6WthYiIqAax66ift956C+vWrUOTJk3w6quvomnTpgCA8+fPY+HChTAajfjnP//plkIl5eULBNYF9L+aT6XvV1vqioiIiGoEu4JKREQEfv75Z7zyyiuYNm2a9bh4QRDQt29fLFy4EBEREW4pVHJhTcxB5c4FoN7jUldDRERUI9h9zt/Y2Fhs3rwZmZmZOHToEA4ePIjMzExs3rwZcXFxDhcyd+5cCIKAiRMnOrwMtworu1L0nfPS1kFERFSDOHxm2pCQEHTo0MElRRw5cgSLFy9G69atXbI8twgzb+ZCxjlp6yAiIqpBJL+KUl5eHkaMGIElS5YgJCRE6nIeLtwyonJB2jqIiIhqEIdHVFxl3LhxGDhwIHr16oV//etflc5bXFyM4uJi63O9Xg/AfC0CV19G3LI863KDG0ALALlpMORmArogl35edSvXn8IovT9A+T0qvT9A+T2yP8/nrh7tWZ4gSnilqNWrV2POnDk4cuQIdDodevTogbZt2+LDDz+scP6ZM2di1qxZ5aavXLkSvr7uv6pxn+QJ8DFkYU+T6cjya+z2zyMiIlKigoICDB8+HDk5ORVelud+ko2o3LhxAxMmTMC2bdug0+mq9J5p06Zh8uTJ1ud6vR4xMTHo06fPIxu1l8FgwLZt29C7d2/r2XjV2V8BKUno0qgWxIQBLv286lZRf0qi9P4A5feo9P4A5ffI/jyfu3q0bBGpCsmCyrFjx5CRkYF27dpZpxmNRuzZsweffvopiouLy10i2tvbG97e3uWWpdVq3fZLYrPsiBZAShI09y4DCvmldOfPTg6U3h+g/B6V3h+g/B7Zn+dzdY/2LEuyoPLUU0/hzJkzNtNeeOEFNGvWDFOmTCkXUmTBcuTPHR75Q0REVB0kCyoBAQFo1aqVzTQ/Pz/Url273HTZsJxLJYPnUiEiIqoOkh+e7FEsIyq5aUBRjrS1EBER1QCSH558v6SkJKlLqJxPMBAQBeTeMp9PJaaj1BUREREpGkdU7BXWzHzPU+kTERG5HYOKvSxnqL19Vto6iIiIagAGFXtFtDTf306Wtg4iIqIagEHFXpHx5vv0M4B0J/UlIiKqERhU7BXWDFBpgKJsQH9T6mqIiIgUjUHFXhpvILSJ+XE6N/8QERG5E4OKIyLKTkiXfqby+YiIiMgpDCqOsOyncptBhYiIyJ0YVBwRaRlR4aYfIiIid2JQcURE2YjKvatASb60tRARESkYg4oj/MMA/0gAIk/8RkRE5EYMKo6ybv45LW0dRERECsag4ijLkT88Qy0REZHbMKg4ynLkzy2OqBAREbkLg4qjohPM97eTAaNB2lqIiIgUikHFUSFxgHcQUFoEZJyTuhoiIiJFYlBxlEoFRLc1P047IWkpRERESsWg4gzL5p+049LWQUREpFAMKs6o0858f5NBhYiIyB0YVJxhGVHJOAsYiqSthYiISIEYVJwRFAP4hgKmUp5PhYiIyA0YVJwhCL9t/uEOtURERC7HoOIsy+Yf7qdCRETkcgwqzormiAoREZG7MKg4yzKicuc8UKSXthYiIiKFYVBxVkAEEFwPgAjcPCZ1NURERIrCoOIKMZ3M9zcOS1sHERGRwjCouII1qByStg4iIiKFYVBxBUtQ+fUIYDJKWwsREZGCMKi4QngLwMsfKNabd6olIiIil2BQcQW1BqjzmPkxN/8QERG5DIOKq9R73HzPHWqJiIhchkHFVWI6mu+vH5S2DiIiIgVhUHGVuh0ACEBWCpCXIXU1REREisCg4iq6IPNOtQBw/YC0tRARESkEg4or1e9qvr+2T9o6iIiIFIJBxZXq/858n7JX2jqIiIgUgkHFlWLLgsqdc0DeHWlrISIiUgAGFVfyqw1EtDI/vsZRFSIiImcxqLha/W7mewYVIiIipzGouBr3UyEiInIZBhVXq98VgADcvQTob0ldDRERkUdjUHE1nxAgMt78OHW/tLUQERF5OAYVd4h7wnx/dZe0dRAREXk4BhV3aNjTfH95JyCK0tZCRETkwRhU3CG2K6DxAXLTgIxzUldDRETksRhU3EGr++3on8vbpa2FiIjIgzGouEujXuZ7BhUiIiKHMai4iyWoXD8AFOdJWwsREZGHYlBxl9oNgeBYwFjCqykTERE5iEHFXQSBm3+IiIicxKDiTpagculHHqZMRETkAAYVd2rQw3yYcvZ14PYvUldDRETkcRhU3MnL97eTv53fJG0tREREHohBxd2aDTTfn/9B2jqIiIg8EIOKuzXpBwgqIP20eRMQERERVRmDirv51QbqdTY/Pr9Z2lqIiIg8DINKdeDmHyIiIocwqFQHS1BJ/RnIz5S2FiIiIg/CoFIdQuoDUW0B0Qic3SBxMURERJ6DQaW6tPqj+f7MWmnrICIi8iAMKtWl1R/M99d/BnJ+lbYWIiIiD8GgUl2C6gL1upgfJ6+TthYiIiIPIWlQeffdd9GhQwcEBAQgPDwcgwcPxoULF6Qsyb3iyzb/JHPzDxERUVVIGlR2796NcePG4eDBg9i2bRsMBgP69OmD/Px8KctynxaDAUEN3DoJZF6WuhoiIiLZ00j54Vu3brV5vmzZMoSHh+PYsWN44oknJKrKjfxCzdf+ubwNOLUSeGqG1BURERHJmqRB5UE5OTkAgFq1alX4enFxMYqLi63P9Xo9AMBgMMBgMLi0FsvyXL1cofVQaC5vg3hiBUp/9yagUrt0+VXlrv7kQun9AcrvUen9Acrvkf15Pnf1aM/yBFEURZd+uoNMJhOeeeYZZGdnY9++fRXOM3PmTMyaNavc9JUrV8LX19fdJbqEymRAn+QJ8Dbm4UCDfyAjqI3UJREREVWrgoICDB8+HDk5OQgMDKx0XtkElVdeeQVbtmzBvn37ULdu3QrnqWhEJSYmBpmZmY9s1F4GgwHbtm1D7969odVqXbps1bZ/Qn14MUxNn4bxT8tcuuyqcmd/cqD0/gDl96j0/gDl98j+PJ+7etTr9QgNDa1SUJHFpp9XX30VP/zwA/bs2fPQkAIA3t7e8Pb2Ljddq9W67ZfELct+bBRweDFUl7ZCVZJj3ndFIu782cmB0vsDlN+j0vsDlN8j+/N8ru7RnmVJetSPKIp49dVXsX79euzcuRNxcXFSllN9IloC0e0AUylwapXU1RAREcmWpEFl3Lhx+Oabb7By5UoEBAQgPT0d6enpKCwslLKs6tHuL+b7I18CJqO0tRAREcmUpEHl888/R05ODnr06IGoqCjrbc2aNVKWVT1aPwfogoGsa8ClbVJXQ0REJEuS7qMik/14peHlZx5V+flj4NAioGk/qSsiIiKSHV7rR0odxgCCCri6C8g4L3U1REREssOgIqWQWKDpAPPjw4ulrYWIiEiGGFSk1ulv5vuTK4G8O9LWQkREJDMMKlKr/zugzmNAaRFwcKHU1RAREckKg4rUBAHo9rr58eEvgcJsScshIiKSEwYVOWjSDwhvAZTkAkeWSF0NERGRbDCoyIFKBfxusvnxgc+A4lxp6yEiIpIJBhW5aPl7oFZDoPCeOawQERERg4psqDVAz7fMj3/+BMjPlLYeIiIiGWBQkZMWg4GoNuZ9VfYukLoaIiIiyTGoyIlKBTyVaH585EsgK1XaeoiIiCTGoCI3DXsCcd0BYwmwbbrU1RAREUmKQUVuBAHo+w4gqIGz3wFXdkldERERkWQYVOQoshXQcaz58ZY3gdISaeshIiKSCIOKXPWYBviGApkXecFCIiKqsRhU5MonGOg9y/w4aS6QfUPScoiIiKTAoCJnbYYDMY8DJXnAxtcAUZS6IiIiomrFoCJnKhXw7EJAowOu7gKOL5e6IiIiomrFoCJ3oY2AnmWHKf/4FjcBERFRjcKg4gkefwWI6WQ+Y+2GVwCTUeqKiIiIqgWDiidQqYFnPwO0fsC1vcCef0tdERERUbVgUPEUoY2Apz8wP06aC1zdLW09RERE1YBBxZO0+TOQMBKACKx9ifurEBGR4jGoeJr+7wER8UD+HWDVUKA4V+qKiIiI3IZBxdN4+QLDVgF+4cDtZGDtWO5cS0REisWg4omCY8xhRaMDLm4Btk7jyeCIiEiRGFQ8Vd32wODPzI8PLwZ2zZG2HiIiIjdgUPFkrf4IDJhvfrzn38De96Wth4iIyMUYVDxdx7FA79nmxztmAfs+kLYeIiIiF2JQUYKuE4DuU82Pt88037jPChERKQCDilI8OQ3oNcv8eN8HwA+TAGOptDURERE5iUFFSX43EXj6QwACcGwpsOJPQGGWxEURERE5jkFFadq/ADz3NaD1Ba7uAr7sBdy5KHVVREREDmFQUaIWzwAv/QQExQB3LwNf9ABOrOB+K0RE5HEYVJQqMh4Yuwuo3w0w5APf/d18fSBuCiIiIg/CoKJk/mHAX74DnpoBCGogeS3waUfgzP84ukJERB6BQUXpVGqg2z+AF38EQpsA+RnA2pegXj0UvsW3pa6OiIioUgwqNUVMB+Bv+4An/wmovaC6ugNPnZsK1fbpQEm+1NURERFViEGlJtF4A93fBF45AFODJ6ESjVAf+hz4qh9wfhOvwkxERLLDoFIThTaCcdh/cbDBJIhaPyD9NLB6OPBRG/P1gvIzpa6QiIgIAINKjXY7KAGlL+8Huk4EfGoBOTfM1wt6vznw7V+A85uB0hKpyyQiohpMI3UBJLGgukDvWUCPacAv64DDS4C048DZ78w3n1rmqzTH/wmo28G8cy4REVE1YVAhM60OaDvcfEs/A5xaDZz5L5B3GziyxHzzCwOa9AWaDgQa9AC8fKWumoiIFI5BhcqLjDffes0CUpKA098CF7YC+XeAE9+YbxofoF4n8wnl4roD0W0BtVbqyomISGEYVOjh1BqgUS/zzWgAUveb91u5sAXIuQ5cTTLf8Dbg5W/eNBSd8NstqC4gCBI3QUREnoxBhapGrTVv7mnQA+g/D7hzHkjZC1zbA1zbZz41/9Vd5puFbygQ1gwIbWw+2VxoEyC0kfkaRNzXhYiIqoBBhewnCEB4c/Ot018Bkwm4nQzcPAqknTDfMs4BBZlA6j7z7X4qDRAYDQTVM4+6BNUFgmMA/wjzfjC+tQG/UPMoDUdkiIhqNAYVcp5KBUS1Nt8sDEVAxlkg8xKQedF8u3vZfDOWANnXzbfKaHTmURm/2oBPCOAdCOgCAe+gsvtA23utH6D1Md+ghbY0HygtBjQaBh4iIg/FoELuodUBddqZb/czGYHcdCDnV/N5W3JumB9n3zBfhyj/rnmn3dJCoLQI0P9qvtn78QAGAMCZVwBBBWh9zQFGUxZktDpA7QWotObNWmqt+blaWzbNy7yPjtqrbD7Nfa9rzMtUqc0Xe7Q+Vv12sz5XV/6aoDIHPcFySiPhvlBleVz2/IHHgtGIWnkXINyoDWi0FbzP8hgPXUbFn1fBZz9MpQHQyfeWGuBXdMscbjUP7KjtTPB0Z832Ki2FT/Edc2jXyOmfYxddtLS0FL7Fd4DsVPf2J9VFVktL4VucAWRds7M/D7oobGkpvA05kpYgp78MqglUaiCojvmGTg+fryTffIbcgkzzfWEWUKQHinPK7vUP3OcChgLAUAgYCiEaCiCIZZcEEE1ASZ75piAaAN0A4JLEhbiJFkAvADgncSFupAXQBwDOSlyIm2gB9AbYnwfTAmgV8jiAYZLVwKBC8uTlZ76FxDr09lKDAVs2bUT/p3pAC0NZiCkqCzJlgcZkMB/NZDSUPS55+HNjCWAq/W2aKAKi0RyCTGX31uemh7wmVjCvsewxAIj3/c/Q8rjsueXxfa+Logn5+fnw8/Ut+7/8g+9H+fc/ZFmVv16ZR8zzyGU8/HUR5vWo0WggVDpa4b4aqvb+Ki6jgtEYEYDRWAq1WuPIeIybOV9RtfYnweZdESKMpUaoNepH/I5WRH5rvCIiRBgFL0lrYFAhxRIFTdm+K8o8v0upwYAdmzdjwIAB0Cqwx1KDAZsV3B+g/B7Zn+crNRhwcvNmREtYA6/1Q0RERLLFoEJERESyxaBCREREssWgQkRERLLFoEJERESyxaBCREREssWgQkRERLLFoEJERESyxaBCREREssWgQkRERLLFoEJERESyxaBCREREssWgQkRERLLFoEJERESypZG6AGeIoggA0Ov1Ll+2wWBAQUEB9Hq9Ii/fzf48n9J7VHp/gPJ7ZH+ez109Wr63Ld/jlfHooJKbmwsAiImJkbgSIiIisldubi6CgoIqnUcQqxJnZMpkMiEtLQ0BAQEQBMGly9br9YiJicGNGzcQGBjo0mXLAfvzfErvUen9Acrvkf15Pnf1KIoicnNzER0dDZWq8r1QPHpERaVSoW7dum79jMDAQMX+AgLsTwmU3qPS+wOU3yP783zu6PFRIykW3JmWiIiIZItBhYiIiGSLQeUhvL29kZiYCG9vb6lLcQv25/mU3qPS+wOU3yP783xy6NGjd6YlIiIiZeOIChEREckWgwoRERHJFoMKERERyVaNCSoLFy5E/fr1odPp0KlTJxw+fLjS+f/73/+iWbNm0Ol0iI+Px+bNm21eF0URM2bMQFRUFHx8fNCrVy9cunTJnS08kj09LlmyBN26dUNISAhCQkLQq1evcvOPHj0agiDY3Pr16+fuNh7Knv6WLVtWrnadTmczj9zWoT399ejRo1x/giBg4MCB1nnktP727NmDQYMGITo6GoIgYMOGDY98T1JSEtq1awdvb280atQIy5YtKzePvX/X7mRvj+vWrUPv3r0RFhaGwMBAdO7cGT/++KPNPDNnziy3Dps1a+bGLh7O3v6SkpIq/B1NT0+3mU8u69De/ir6+xIEAS1btrTOI6f19+6776JDhw4ICAhAeHg4Bg8ejAsXLjzyfXL4LqwRQWXNmjWYPHkyEhMTcfz4cbRp0wZ9+/ZFRkZGhfP//PPPGDZsGF566SWcOHECgwcPxuDBg5GcnGyd57333sPHH3+MRYsW4dChQ/Dz80Pfvn1RVFRUXW3ZsLfHpKQkDBs2DLt27cKBAwcQExODPn364ObNmzbz9evXD7du3bLeVq1aVR3tlGNvf4D5BEX3156ammrzupzWob39rVu3zqa35ORkqNVqDBkyxGY+uay//Px8tGnTBgsXLqzS/CkpKRg4cCCefPJJnDx5EhMnTsSYMWNsvsgd+Z1wJ3t73LNnD3r37o3Nmzfj2LFjePLJJzFo0CCcOHHCZr6WLVvarMN9+/a5o/xHsrc/iwsXLtjUHx4ebn1NTuvQ3v4++ugjm75u3LiBWrVqlfsblMv62717N8aNG4eDBw9i27ZtMBgM6NOnD/Lz8x/6Htl8F4o1QMeOHcVx48ZZnxuNRjE6Olp89913K5z/ueeeEwcOHGgzrVOnTuLLL78siqIomkwmMTIyUvz3v/9tfT07O1v09vYWV61a5YYOHs3eHh9UWloqBgQEiMuXL7dOGzVqlPjss8+6ulSH2Nvf0qVLxaCgoIcuT27r0Nn198EHH4gBAQFiXl6edZqc1t/9AIjr16+vdJ4333xTbNmypc20P//5z2Lfvn2tz539mblTVXqsSIsWLcRZs2ZZnycmJopt2rRxXWEuUpX+du3aJQIQs7KyHjqPXNehI+tv/fr1oiAI4rVr16zT5Lr+RFEUMzIyRADi7t27HzqPXL4LFT+iUlJSgmPHjqFXr17WaSqVCr169cKBAwcqfM+BAwds5geAvn37WudPSUlBenq6zTxBQUHo1KnTQ5fpTo70+KCCggIYDAbUqlXLZnpSUhLCw8PRtGlTvPLKK7h7965La68KR/vLy8tDbGwsYmJi8Oyzz+KXX36xviandeiK9fef//wHQ4cOhZ+fn810Oaw/Rzzqb9AVPzO5MZlMyM3NLfc3eOnSJURHR6NBgwYYMWIErl+/LlGFjmnbti2ioqLQu3dv7N+/3zpdaevwP//5D3r16oXY2Fib6XJdfzk5OQBQ7vftfnL5LlR8UMnMzITRaERERITN9IiIiHLbSi3S09Mrnd9yb88y3cmRHh80ZcoUREdH2/zC9evXD19//TV27NiBefPmYffu3ejfvz+MRqNL638UR/pr2rQpvvrqK3z33Xf45ptvYDKZ0KVLF/z6668A5LUOnV1/hw8fRnJyMsaMGWMzXS7rzxEP+xvU6/UoLCx0ye+83MyfPx95eXl47rnnrNM6deqEZcuWYevWrfj888+RkpKCbt26Wa8cL2dRUVFYtGgR1q5di7Vr1yImJgY9evTA8ePHAbjm3y25SEtLw5YtW8r9Dcp1/ZlMJkycOBFdu3ZFq1atHjqfXL4LPfqihOQac+fOxerVq5GUlGSzw+nQoUOtj+Pj49G6dWs0bNgQSUlJeOqpp6Qotco6d+6Mzp07W5936dIFzZs3x+LFi/H2229LWJnr/ec//0F8fDw6duxoM92T119Ns3LlSsyaNQvfffedzT4c/fv3tz5u3bo1OnXqhNjYWHz77bd46aWXpCi1ypo2bYqmTZtan3fp0gVXrlzBBx98gP/3//6fhJW53vLlyxEcHIzBgwfbTJfr+hs3bhySk5Ml21/GXoofUQkNDYVarcbt27dtpt++fRuRkZEVvicyMrLS+S339izTnRzp0WL+/PmYO3cufvrpJ7Ru3brSeRs0aIDQ0FBcvnzZ6Zrt4Ux/FlqtFgkJCdba5bQOnekvPz8fq1evrtI/elKtP0c87G8wMDAQPj4+LvmdkIvVq1djzJgx+Pbbb8sNsz8oODgYTZo08Yh1WJGOHTtaa1fKOhRFEV999RVGjhwJLy+vSueVw/p79dVX8cMPP2DXrl2oW7dupfPK5btQ8UHFy8sLjz32GHbs2GGdZjKZsGPHDpv/cd+vc+fONvMDwLZt26zzx8XFITIy0mYevV6PQ4cOPXSZ7uRIj4B5b+23334bW7duRfv27R/5Ob/++ivu3r2LqKgol9RdVY72dz+j0YgzZ85Ya5fTOnSmv//+978oLi7G888//8jPkWr9OeJRf4Ou+J2Qg1WrVuGFF17AqlWrbA4tf5i8vDxcuXLFI9ZhRU6ePGmtXSnrcPfu3bh8+XKV/rMg5foTRRGvvvoq1q9fj507dyIuLu6R75HNd6HLdsuVsdWrV4ve3t7ismXLxLNnz4p//etfxeDgYDE9PV0URVEcOXKkOHXqVOv8+/fvFzUajTh//nzx3LlzYmJioqjVasUzZ85Y55k7d64YHBwsfvfdd+Lp06fFZ599VoyLixMLCwurvT9RtL/HuXPnil5eXuL//vc/8datW9Zbbm6uKIqimJubK77++uvigQMHxJSUFHH79u1iu3btxMaNG4tFRUWy72/WrFnijz/+KF65ckU8duyYOHToUFGn04m//PKLdR45rUN7+7P43e9+J/75z38uN11u6y83N1c8ceKEeOLECRGA+P7774snTpwQU1NTRVEUxalTp4ojR460zn/16lXR19dXfOONN8Rz586JCxcuFNVqtbh161brPI/6mVU3e3tcsWKFqNFoxIULF9r8DWZnZ1vn+cc//iEmJSWJKSkp4v79+8VevXqJoaGhYkZGhuz7++CDD8QNGzaIly5dEs+cOSNOmDBBVKlU4vbt263zyGkd2tufxfPPPy926tSpwmXKaf298sorYlBQkJiUlGTz+1ZQUGCdR67fhTUiqIiiKH7yySdivXr1RC8vL7Fjx47iwYMHra91795dHDVqlM383377rdikSRPRy8tLbNmypbhp0yab100mkzh9+nQxIiJC9Pb2Fp966inxwoUL1dHKQ9nTY2xsrAig3C0xMVEURVEsKCgQ+/TpI4aFhYlarVaMjY0Vx44dK9mXgCja19/EiROt80ZERIgDBgwQjx8/brM8ua1De39Hz58/LwIQf/rpp3LLktv6sxyq+uDN0tOoUaPE7t27l3tP27ZtRS8vL7FBgwbi0qVLyy23sp9ZdbO3x+7du1c6vyiaD8mOiooSvby8xDp16oh//vOfxcuXL1dvY2Xs7W/evHliw4YNRZ1OJ9aqVUvs0aOHuHPnznLLlcs6dOR3NDs7W/Tx8RG/+OKLCpcpp/VXUW8AbP6u5PpdyKsnExERkWwpfh8VIiIi8lwMKkRERCRbDCpEREQkWwwqREREJFsMKkRERCRbDCpEREQkWwwqREREJFsMKkRERCRbDCpEREQkWwwqRORSo0ePLne5++o0cuRIvPPOO1Wad+jQoViwYIGbKyIiZ/AU+kRUZYIgVPp6YmIiJk2aBFEUERwcXD1F3efUqVPo2bMnUlNT4e/v/8j5k5OT8cQTTyAlJQVBQUHVUCER2YtBhYiqLD093fp4zZo1mDFjBi5cuGCd5u/vX6WA4C5jxoyBRqPBokWLqvyeDh06YPTo0Rg3bpwbKyMiR3HTDxFVWWRkpPUWFBQEQRBspvn7+5fb9NOjRw+89tprmDhxIkJCQhAREYElS5YgPz8fL7zwAgICAtCoUSNs2bLF5rOSk5PRv39/+Pv7IyIiAiNHjkRmZuZDazMajfjf//6HQYMG2Uz/7LPP0LhxY+h0OkREROBPf/qTzeuDBg3C6tWrnf/hEJFbMKgQkdstX74coaGhOHz4MF577TW88sorGDJkCLp06YLjx4+jT58+GDlyJAoKCgAA2dnZ6NmzJxISEnD06FFs3boVt2/fxnPPPffQzzh9+jRycnLQvn1767SjR49i/PjxmD17Ni5cuICtW7fiiSeesHlfx44dcfjwYRQXF7uneSJyCoMKEbldmzZt8NZbb6Fx48aYNm0adDodQkNDMXbsWDRu3BgzZszA3bt3cfr0aQDAp59+ioSEBLzzzjto1qwZEhIS8NVXX2HXrl24ePFihZ+RmpoKtVqN8PBw67Tr16/Dz88PTz/9NGJjY5GQkIDx48fbvC86OholJSU2m7WISD4YVIjI7Vq3bm19rFarUbt2bcTHx1unRUREAAAyMjIAmHeK3bVrl3WfF39/fzRr1gwAcOXKlQo/o7CwEN7e3jY7/Pbu3RuxsbFo0KABRo4ciRUrVlhHbSx8fHwAoNx0IpIHBhUicjutVmvzXBAEm2mWcGEymQAAeXl5GDRoEE6ePGlzu3TpUrlNNxahoaEoKChASUmJdVpAQACOHz+OVatWISoqCjNmzECbNm2QnZ1tnefevXsAgLCwMJf0SkSuxaBCRLLTrl07/PLLL6hfvz4aNWpkc/Pz86vwPW3btgUAnD171ma6RqNBr1698N577+H06dO4du0adu7caX09OTkZdevWRWhoqNv6ISLHMagQkeyMGzcO9+7dw7Bhw3DkyBFcuXIFP/74I1544QUYjcYK3xMWFoZ27dph37591mk//PADPv74Y5w8eRKpqan4+uuvYTKZ0LRpU+s8e/fuRZ8+fdzeExE5hkGFiGQnOjoa+/fvh9FoRJ8+fRAfH4+JEyciODgYKtXD/9kaM2YMVqxYYX0eHByMdevWoWfPnmjevDkWLVqEVatWoWXLlgCAoqIibNiwAWPHjnV7T0TkGJ7wjYgUo7CwEE2bNsWaNWvQuXPnR87/+eefY/369fjpp5+qoToicgRHVIhIMXx8fPD1119XemK4+2m1WnzyySduroqInMERFSIiIpItjqgQERGRbDGoEBERkWwxqBAREZFsMagQERGRbDGoEBERkWwxqBAREZFsMagQERGRbDGoEBERkWwxqBAREZFs/X9e87gr/FXe8wAAAABJRU5ErkJggg=="]},"metadata":{}}],"source":["#ODE:\n","def rate_equations(y, t, k_tau1, k_tau2):\n"," L1, L2 = y # concentrations\n"," # rate updates:\n","\n"," #rate tautomer 1 per time:\n"," dL1dt = k_tau2 * L2 - k_tau1 * L1\n","\n"," #rate tautomer 2 per time:\n"," dL2dt = k_tau1 * L1 - k_tau2 * L2 \n"," \n"," return [dL1dt, dL2dt]\n","\n","# initialise concentrations to some starting value:\n","L1_0 = 5e-6 # 5 μM\n","L2_0 = 5e-6 # 5 μM\n","\n","# set some rates for the tautomer transition:\n","k_tau1 = 0.5 # in M^-1 s^-1 #this could be considered the off-rate\n","k_tau2 = 10 # in s^-1 #which makes this the on-rate. Remember the reaction is reversible\n"," # so on- and off-rates both happen at same time. Molar Units in the 'on' rate are a convention.\n","# Initial conditions\n","y0 = [L1_0, L2_0]\n","\n","# Time points for the simulation\n","t = np.linspace(0, 2, 1000) # 2 second simulation. It's fast, so 2s is all we need!\n","\n","# Integrate the rate equations\n","y = odeint(rate_equations, y0, t, args=(k_tau1, k_tau2))\n","\n","# Extract the concentrations\n","L1 = y[:, 0]\n","L2 = y[:, 1]\n","plt.plot(t, L1, label='Tautomer 1')\n","plt.plot(t, L2, label='Tautomer 2')\n","plt.legend()\n","plt.ylabel('Conc. (M)')\n","plt.xlabel('Time (s)')\n","plt.grid()"],"metadata":{}},{"id":"836a0e8e-8e4a-4f85-a137-e14b4534a3bd","cell_type":"markdown","source":["Let's plot it as % populations instead. At equilibrium, these % populations are also known as the 'f' values of each tautomer. \n"],"metadata":{},"attachments":{}},{"id":"c02e33e2-e062-448c-9564-5e832d4a0251","cell_type":"code","execution_count":3,"outputs":[{"output_type":"execute_result","execution_count":null,"data":{"text/plain":["(0.0, 100.0)"]},"metadata":{}},{"output_type":"display_data","data":{"text/plain":["<Figure size 640x480 with 1 Axes>"],"image/png":["iVBORw0KGgoAAAANSUhEUgAAAjsAAAG2CAYAAACZEEfAAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjkuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy80BEi2AAAACXBIWXMAAA9hAAAPYQGoP6dpAABrwElEQVR4nO3dd3hT5dsH8G+SJulu6W4ZpVBG2SDCj1nAQhmC4EAQFQEXoggIKq/IEkUQFJUlKkNlylIBQYQCyt5Q9ijL0hYodI80Oe8foYeGNiFpkyY5/X6uK1eSkzsn99OTcfc5z3mOTBAEAUREREQSJbd3AkRERES2xGKHiIiIJI3FDhEREUkaix0iIiKSNBY7REREJGksdoiIiEjSWOwQERGRpLHYISIiIkljsUNERESSxmKHiIiIJM2uxc6uXbvQs2dPhIWFQSaTYf369QaPC4KA8ePHIzQ0FG5uboiJicGFCxcMYlJTUzFgwAB4e3vD19cXQ4YMQWZmZjm2goiIiByZXYudrKwsNG7cGHPmzCnx8enTp+Obb77B/PnzsX//fnh4eCA2Nha5ublizIABA3Dq1Cls3boVGzZswK5du/D666+XVxOIiIjIwckc5USgMpkM69atQ+/evQHoe3XCwsLw3nvvYfTo0QCAtLQ0BAcHY/HixejXrx/OnDmDevXq4eDBg2jevDkAYPPmzejevTtu3LiBsLAwezWHiIiIHISLvRMwJiEhAUlJSYiJiRGX+fj4oGXLlti7dy/69euHvXv3wtfXVyx0ACAmJgZyuRz79+9Hnz59Slx3Xl4e8vLyxPs6nQ6pqanw9/eHTCazXaOIiIjIagRBQEZGBsLCwiCXG99Z5bDFTlJSEgAgODjYYHlwcLD4WFJSEoKCggwed3FxgZ+fnxhTkqlTp2LSpElWzpiIiIjs4fr166hSpYrRxx222LGlsWPHYtSoUeL9tLQ0VKtWDQkJCfDy8rLa62g0GsTFxaFjx45QKpVWW68jkXob2T7nJ/U2sn3OT+pttGX7MjIyEBER8cjfboctdkJCQgAAycnJCA0NFZcnJyejSZMmYkxKSorB8woKCpCamio+vyRqtRpqtbrYcj8/P3h7e1shez2NRgN3d3f4+/tL8g0MSL+NbJ/zk3ob2T7nJ/U22rJ9het71BAUh51nJyIiAiEhIdi2bZu4LD09Hfv370erVq0AAK1atcK9e/dw+PBhMWb79u3Q6XRo2bJluedMREREjseuPTuZmZm4ePGieD8hIQHHjh2Dn58fqlWrhhEjRmDKlCmoVasWIiIi8PHHHyMsLEw8YisqKgpdu3bFa6+9hvnz50Oj0eDtt99Gv379eCQWERERAbBzsXPo0CF07NhRvF84jmbgwIFYvHgx3n//fWRlZeH111/HvXv30LZtW2zevBmurq7ic5YuXYq3334bTzzxBORyOZ555hl888035d4WIiIickx2LXY6dOgAU9P8yGQyTJ48GZMnTzYa4+fnh2XLltkiPSIiIpIAhx2zQ0RERGQNLHaIiIhI0ljsEBERkaSx2CEiIiJJY7FDREREksZih4iIiCSNxQ4RERFJGosdIiIikjQWO0RERCRpDnvWc6KKQBAEaHUCdAKgEwToit7X3b8vCBAE3F8uQKdDkeUCtIX3dUKR9QIC9M8DAOH+az24rb9VUKDF5XTg0NW7UChcxJyEh9YDg/XcXybeNlz3g1j965uYJP1Bvmb8nUr7fG2BFidSZXA5nSy2sTRZPKodZjTTjHWYsxZD2gItjt6WASeToHBRWPx8W5PB9NmoH0WrLcDROzLI4pMesf2s4xEnz7aJgoICHLvfRhcXy9poh3QtVqDV4tgdGdrnFaCSnc7qzmKniKysLCgUxb8sFAqFwfm4srKyjK5DLpfDzc1NvJ+bm4usrKwST2v/cGx2drbRL3WZTAZ3d/dSxebk5ECn0xnN2cPDo1Sxubm54qWkNj4cq9Vqja7X3d0dsvvfMnl5eSgoKLBKrJubG+RyfQdmfn4+NBqNweMFWh0y8wqQmVuAfJkLcgsE5ORrkZ6dg6ycPGTl5uPYlTxc+usU8rVAXoEWORotCuCCPJ0M+QVa5OXlIy8/HwVaARqt7v5FQIFWhwJBQAFcoIUMGq2A/Lx85GvyodEaFieFZC5KyOT696CgLYCgNd42g1idFkKBxniswgWywmKmpNij/5gfa7BeBWQKpeWxgg6CJt86sXIFZC6FsQIETV7JgSf3mx8LQCaXQ+aiEu/r8nOtEguZDHKlunSxmlzjVdXpA5ArXc2LleGh2DyTlZhcVbpYoSAfgonvE0tiF507Ln7uhQINBJ3x7xOZUm1BrAoymf47QtBqIJj4nrIo1uCzbF7sovMnLPvcl+d3RKljCz/LCvS9lw2VzPg2ViqVUKn0nyOdToecnByzYs0hEx71L1MFkJ6eDh8fH6OPd+/eHRs3bhTve3h4IDs7u8TY6Oho7NixAwCg0WgQEBCA9PT0EmObN2+OgwcPiverV6+Oq1evlhhbr149nDp1Srxfv359nD59usTY8PBwXLlyRbz/+OOP49ChQyXGBgQE4NatW+L9Dh06YOfOnSXGuru7GxR6PXr0wKZNm0qMBQz/G3/uueewevVqo7GZmZlicfTKK69gyZIlRmNTUlIQGBgIABg2bBjmzp1rNHbSsjjIvIKQmpWPvxbNwOktS43Ghg6eA1VgOADg3r9LkbZ7udHYkJe/hDq0NgAgbf8a3NuxyGhscP/P4FqtEQAg48gGpG6dbzQ28NkJcK/5OAAg8+TfuLNpltHYas/+H/waRkMuk+He6V24vGKK0djIZ8cguHlXyGRA6pl9OL34I6OxtfoMR9U2fSCTyXD34lEcmTfSaGydXkNRo1N/yGRA2rUz2D3zDeOx3Qahbo8hAID0m5cR9+nLxvN9oj8aPD0MAJB15ya2jn/OaGxE+z5o8vx7kMlkyMu4i40fPGk0Nvx/3dD85XEAgIK8HPw2MsZobOVmHdHqtQd/09VD2xiNDWnQCu2GzRT/zV47vBO0RoqYwFpN0fG9OeL930Z3R17mvRJjK4XXRZf/Wyje/+P/nkb2naQSY71Dq6PbxAfnCfxz4gCk30woMdbdPwQ9P1sr3v/rs8G4e/VsibFqT1/0nvngc7595jDcOn+0xFiFyhXPfrtdvL/r2/dwM35vibEA0Hf+HvH2ngUf4caROKOxfWb9DaWr/p+4A4un4Mo+4989vb7YCFevSgCAw8tn4NLOtUZje0xZA4+AUADAsTWzcX6r8XMtdhn/C3zCagAATv3xA05vXGg09okPf4Bf9XoAgHN/LcWJtXOMxrYf+S1c/KvDz98Pl3auxdEVM43Gth32BUIb6t+LV/ZsxMGfPjUa+79Xp6DqY50AANcPb8e+H8YZjX385Y9QvVUPAMDNk7vx79wxRmObPv8eIjs8AwBIOX8EO79622hsoz7DUKtzf9xNvYsRLTzRq0tHo7ETJkzAxIkTAQCnTp1CgwYNjMaOHj0aX3zxhfj7nZaWBm9vb6PxEEhIS0sTcL83vqRL9+7dDeLd3d2NxkZHR4tx+fn5gre3t9HY5s2bG6w3PDzcaGy9evUMYuvVq2c0Njw83CC2efPmRmMDAgIMYqOjo43Guru7G8R2797d5N+tqGeffdZkbGZmphg7cOBAk7Gr/40Xvt91SZj0+ymh3hPPmYyt/OaPQvgHG4TwDzYI3i2eNhlb/53vhejp24Wus3YJdboPMhk7Zu4a4Yd/Lgs/770iDHhnrMnYBSt+F07euCecS0oXJk6daTJ2zbrfhJz8AiFPoxV+/HGhydhVq1aJf7NVq1aZjF20aJEYu2HDBpOxs2fPFmPj4uJMxk6fPl2MPXDggMnYCRMmiLHx8fEmY0ePHi3GJiQkmIx96623xNiUlBSTsQMHDhRjMzMzTcY+++yzBu9hU7Gl/Y4QBEEICAgwGmvJd0RUVJRBrNS+I+7evSvGPuo7IiUlRYx96623TMYmJCSIsaNHjzYZGx8fL8ZOmDDBZOyBAwfE2OnTp5uM3bp1q7B+/XohPz9fmD17tsnYDRs2iOtdtGiRyVhH+Y7Iz88X1q9fL+zZs8dkbGm+Iwp/v9PS0gRT2LODBz07iYmJJVaGpd2NpdFosHbtWsTGxkp6N9aWLVtKbGNpd2Pl5uYiMTUL8f+lIf5mGi6mZOLKrSxcTc2GRiuY7KJ2Uyrg56mEn7sKfp5qBPl6IcDLFX4eKnirAHcXGTxdFfByVcJL7QJPVyU81S5QuchL3OWl0WhKbJ+rq6u4y7Ok3WNFFY3VaDTIzze+S0atVov77C2JLSgoQF6e8V0yKpVKzL9obEntKxqr1WqRm2t8N0vRrmRLYi3pon5UrIuLC9Rq/a4eQRCK9boWbaObm5vJ2KIs+dyXZVe3JbElfe4L29e1a1eDHmpH+Y4w9bk3J7awfX369BHfE+W5q7u0sZZ8RygUCmzZsgXdu3cX440p7++IR8Wa87mXyWTYtGkTYmNjTb4fSvMdYW7PDsfsFOHh4WHw4TMVZy5XV1d4eHiUWOw8rOiXjzVji35ZWjO28MNsThuL/hA8rECrw4kbadh7+Q4OJKTixI003M4s4YOmUMPdVY6IAE/UCPBAlUpuCPN1Q2XfB9febi7il1xZqFQqqFQqaDSaR7avMNYcSqXSrPeCpbEuLi5mD2wsGvuo9ikUCrPf75bEyuVym8TKZLJiscbaWFKsKY4QW9LnvrB9Dz/mKN8RZY0tbF/Rz7VarRaL1kexJNaSz7I1Y4sWQo72HfEo5nzuC9v38D8FpljyuTcHix2yi+up2dh6Ohm7L97GgYRUZOQZ/uelkMtQK8gTDSv7ICrUG5FBnqgR6IEwHzfI5c5w/AERETkKFjtULgRBwPEbadh6Ogl/n07BueQMg8e9XF3QMsIf/6vhh6bVKqFeqDfcVI53GC0RETkfFjtkU5dvZWLd0f+w7uh/uHH3wf5XhVyGFtX90LFuIFrVCEC9MG8o2GNDREQ2wGKHrC4jV4P1R//D6iP/4fj1e+JyD5UCHeoGoXNUMDrUCYSvu/lzJBAREZUWix2ymvPJGfh571WsPXIDWfn6EfcKuQztawWgd9PK6FIvhLumiIio3LHYoTJLzAJeXHgQ+xPuistqBnrghZbh6NU4DIFe5h0JQUREZAssdqjU8gt0WLL3Kr4+pUCu9i4Uchk6RwXj5VbhaFXT3yqHgBMREZUVix0qlX2X7+CjdSdx6VYWABkaVfbG3BcfQ5VK5s/tQUREVB5Y7JBFUrPy8dmmM1h9+AYAwN9DhZjgHEx8uQXcXLm7ioiIHA+LHTJb3NkUjFl9HLcz8yGTAQNaVsPITjXxb9xWuCjk9k6PiIioRCx26JFyNVp8/udZLN5zBQBQO9gTU59uhMfCK5k83wsREZEjYLFDJt1My8EbPx/GiRtpAIBBbarjg6514arkIeREROQcWOyQUUeu3cUbPx/GrYw8VHJX4su+TdCxbpC90yIiIrIIix0q0YYTiRi18jjytTrUDfHC9y83R1U/HmlFRETOh8UOFbNs/zV8tP4kBAHoUi8YXz3fBB5qvlWIiMg58ReMDMzbcQnTNp8FoD/aavJTDXiCTiIicmosdkg0f+eDQmdYx5oY3aUOZ0EmIiKnx2KHAABL9lzB53/qC50xsXUwrGOknTMiIiKyDs4ER1h16Dom/H4KAPBOp0gWOkREJCksdiq4fy7cwti1JwEAQ9pGYFTn2nbOiIiIyLpY7FRgF1My8NbSI9DqBPRpWhnjekRxjA4REUkOi50KKjUrH4MXH0JGbgGah1fC5880ZKFDRESSxGKnAtLqBAxffhTXUrNRzc8d3730GNQuPP0DERFJE4udCmj29ov49+JtuCkV+GFgc/h7qu2dEhERkc2w2Klg9ly8jVnbzgMApvRugNrBXnbOiIiIyLZY7FQgadkajFx1DIIA9G1eBc88VsXeKREREdkci50KZPKG00hOz0ONAA9M6tXA3ukQERGVCxY7FcTfp5Ox5sgNyGTAF881gpuKA5KJiKhiYLFTAaRla/B/6/QTB77aNgKPhfvZOSMiIqLyw2KnApj65xmkZOShRqAH3utSx97pEBERlSsWOxJ37Po9rDx0HQAw7ZlGcFVy9xUREVUsLHYkTKcTMP63eAgC8HSzyni8OndfERFRxcNiR8JWHrqOEzfS4KV2wYfd6to7HSIiIrtgsSNRadkaTN98FgAwonNtBHm52jkjIiIi+2CxI1Fzd1zE3WwNagd74uVW4fZOh4iIyG5Y7EjQzbQcLN5zBQDwYbe6UCq4mYmIqOLir6AEff33BeQV6NCiuh861gmydzpERER2xWJHYi6mZGLV/UPNP+hWFzKZzM4ZERER2ReLHYn5dvsF6ASgc71gPBZeyd7pEBER2R2LHQm5cjsLfxxPBACMiKll52yIiIgcA4sdCZm34xJ0AtCpbhDqh/nYOx0iIiKHwGJHIhLv5WDt0RsAgGEdI+2cDRERkeNgsSMRC3ZdhkYroFUNf47VISIiKoLFjgSk5WjEI7De6ljTztkQERE5FhY7EvDroevIzteiTrAX2kYG2DsdIiIih8Jix8lpdQKW7L0CAHilTXXOq0NERPQQFjtObvvZFFxPzYGPmxK9m1S2dzpEREQOh8WOk1u0OwEA0K9FVbipFHbOhoiIyPE4dLGj1Wrx8ccfIyIiAm5ubqhZsyY++eQTCIIgxgiCgPHjxyM0NBRubm6IiYnBhQsX7Jh1+bl8KxN7Lt2BXAa83Kq6vdMhIiJySA5d7EybNg3z5s3D7NmzcebMGUybNg3Tp0/Ht99+K8ZMnz4d33zzDebPn4/9+/fDw8MDsbGxyM3NtWPm5WPl/SOwOtQJQmVfNztnQ0RE5Jhc7J2AKXv27MFTTz2FHj16AACqV6+O5cuX48CBAwD0vTqzZs3CuHHj8NRTTwEAfvrpJwQHB2P9+vXo16+f3XK3NY1WhzWH/wMA9G1e1c7ZEBEROS6HLnZat26NBQsW4Pz586hduzaOHz+Of//9F19++SUAICEhAUlJSYiJiRGf4+Pjg5YtW2Lv3r1Gi528vDzk5eWJ99PT0wEAGo0GGo3GavkXrsua6yz095kU3M7Mg7+HCu0jK9nkNcxhyzY6ArbP+Um9jWyf85N6G23ZPnPXKROKDoBxMDqdDv/3f/+H6dOnQ6FQQKvV4tNPP8XYsWMB6Ht+2rRpg8TERISGhorP69u3L2QyGVauXFnieidOnIhJkyYVW75s2TK4u7vbpjFW9v1ZOeLvytEpVIenquvsnQ4REVG5y87OxgsvvIC0tDR4e3sbjXPonp1Vq1Zh6dKlWLZsGerXr49jx45hxIgRCAsLw8CBA0u93rFjx2LUqFHi/fT0dFStWhVdunQx+ceylEajwdatW9G5c2colUqrrTclIw+j9u8CIOD959qhZqCH1dZtKVu10VGwfc5P6m1k+5yf1Ntoy/YV7pl5FIcudsaMGYMPP/xQ3B3VsGFDXL16FVOnTsXAgQMREhICAEhOTjbo2UlOTkaTJk2MrletVkOtVhdbrlQqbfJGs/Z6/zx1HVqdgGbVfFE3zNdq6y0LW/3tHAXb5/yk3ka2z/lJvY22aJ+563Poo7Gys7MhlxumqFAooNPpd9tEREQgJCQE27ZtEx9PT0/H/v370apVq3LNtTz9fjwRANC7KScRJCIiehSH7tnp2bMnPv30U1SrVg3169fH0aNH8eWXX2Lw4MEAAJlMhhEjRmDKlCmoVasWIiIi8PHHHyMsLAy9e/e2b/I2knA7CydupEEhl6F7w9BHP4GIiKiCc+hi59tvv8XHH3+Mt956CykpKQgLC8Mbb7yB8ePHizHvv/8+srKy8Prrr+PevXto27YtNm/eDFdXVztmbjt/3O/VaV3THwGexXfFERERkSGHLna8vLwwa9YszJo1y2iMTCbD5MmTMXny5PJLzE4EQcBvx/Rz6zzF82ARERGZxaHH7JCh0zfTcelWFlQucsTWD7Z3OkRERE6BxY4T2XDiJgCgU50geLlKd8Q+ERGRNbHYcSJ/nUoCAHRrGGLnTIiIiJwHix0ncTElE5duZUGpkKFj3SB7p0NEROQ0WOw4ib9O63t1WtcMgDd3YREREZmNxY6T+OtUMgCgCwcmExERWYTFjhNISsvFsev3IJMBnaNY7BAREVmCxY4T2HpG36vTtKovgrylOVkiERGRrbDYcQKFR2F1qc+jsIiIiCzFYsfBZecXYP/lVABATBSPwiIiIrIUix0Ht/9yKvK1OlT2dUPNQE97p0NEROR0WOw4uB3nUgAA0XUCIZPJ7JwNERGR82Gx4+B2nr8FAIiuHWjnTIiIiJwTix0HduV2Fq7cyYaLXIY2kQH2ToeIiMgpsdhxYIW9Os2rV4Kn2sXO2RARETknFjsO7MEuLB6FRUREVFosdhxUXoEWey/dAcDxOkRERGXBYsdBHbt2DzkaLQI8VYgK9bJ3OkRERE6LxY6D2ntZ36vzvxr+POSciIioDFjsOKjCXVitavrbORMiIiLnxmLHAeVqtDh67R4AoFUNFjtERERlwWLHAR2+ehf5Wh2CvdWICPCwdzpEREROjcWOAxJ3YXG8DhERUZmx2HFAhYOTOV6HiIio7FjsOJisvAIcv34PANC6Jk8RQUREVFYsdhzM4at3UaATUNnXDVX93O2dDhERkdNjseNgDl29CwBoGeFn50yIiIikgcWOgzl8NRUA0Cy8kp0zISIikgYWOw6kQKvDsfvz6zSvzmKHiIjIGljsOJCzSRnIytfCS+2CWkE8HxYREZE1sNhxIEeu6cfrNA2vBIWc8+sQERFZA4sdB3Loir7Yeawad2ERERFZC4sdB3L4/pFYHK9DRERkPWUqdvLy8qyVR4WXlJaL/+7lQC4DGlf1tXc6REREkmFRsfPnn39i4MCBqFGjBpRKJdzd3eHt7Y3o6Gh8+umnSExMtFWeklfYqxMV6g1PtYudsyEiIpIOs4qddevWoXbt2hg8eDBcXFzwwQcfYO3atdiyZQt++OEHREdH4++//0aNGjXw5ptv4tatW7bOW3IKi53HOL8OERGRVZnVhTB9+nR89dVX6NatG+Ty4vVR3759AQD//fcfvv32W/zyyy8YOXKkdTOVuBM37gEAmnAXFhERkVWZVexs2bIF3t7ej4yrXLkyPv/88zInVdEUaHWIT0wDADSq4mvfZIiIiCTGrN1YlSpVQkpKCgCgU6dOuHfvni1zqnAupGQiV6ODl9oFNQI87J0OERGRpJhV7Hh6euLOnTsAgB07dkCj0dg0qYqmcBdWg8o+kHMyQSIiIqsyazdWTEwMOnbsiKioKABAnz59oFKpSozdvn279bKrIE7cKNyF5WPnTIiIiKTHrGLnl19+wZIlS3Dp0iXs3LkT9evXh7u7u61zqzAeFDu+9k2EiIhIgswqdtzc3PDmm28CAA4dOoRp06bB19fXlnlVGHkFWpxNSgfAnh0iIiJbsHj2uri4OFvkUWGduZkBjVaAn4cKVSq52TsdIiIiyeG5seyscHByw8o+kMk4OJmIiMjaWOzYWeF4ncbchUVERGQTLHbs7CQHJxMREdkUix07ytVocfFWJgCgfuVHz1BNRERElmOxY0cXUzKh1QnwdVcixNvV3ukQERFJktWKnaioKCgUCmutrkI4nag/5LxeqDcHJxMREdmIxYeeGzN16lSkpaVZa3UVwumb+mInKpS7sIiIiGzFasVO7969rbWqCqOw2KnHYoeIiMhmOGbHTgRBwBn27BAREdlcqXp2Vq9ejVWrVuHatWvIz883eOzIkSNWSUzqbtzNQUZuAZQKGSKDPO2dDhERkWRZ3LPzzTffYNCgQQgODsbRo0fRokUL+Pv74/Lly+jWrZstcpSkwl6dyCAvqFzYwUZERGQrFv/Kzp07FwsWLMC3334LlUqF999/H1u3bsXw4cM5QNkCDwYne9k5EyIiImmzuNi5du0aWrduDUB/NvSMjAwAwEsvvYTly5dbNzsJO8PByUREROXC4mInJCQEqampAIBq1aph3759AICEhAQIgmDd7CSMR2IRERGVD4uLnU6dOuH3338HAAwaNAgjR45E586d8fzzz6NPnz5WT1CKMnI1uJ6aA4BHYhEREdmaxUdjLViwADqdDgAwbNgw+Pv7Y8+ePejVqxfeeOMNqycoRRdS9OfDCvJSo5KHys7ZEBE5B61WC41GY+80rE6j0cDFxQW5ubnQarX2TsfqytI+pVJplbMzWFzsyOVyyOUPOoT69euHfv36lTmRiuRCsn6cU+1gDk4mIjJHcnKyOEZUagRBQEhICK5fvy7JUweVtX2+vr4ICQkp09/GajMok/nOJ+t7dmoFc34dIqJH8fLyQnp6OoKDg+Hu7i65gkCn0yEzMxOenp4GnQlSUdr2CYKA7OxspKSkAABCQ0NLnYPVip2oqCicP39ekl1w1naePTtERGbRarXw8vJCYGAg/P397Z2OTeh0OuTn58PV1VWyxU5p2+fm5gYASElJQVBQUKl3aVntrzp16lQsXLjQWqsT/ffff3jxxRfh7+8PNzc3NGzYEIcOHRIfFwQB48ePR2hoKNzc3BATE4MLFy5YPQ9runh/zE4tzpxMRGRSQUEB5HI53N3d7Z0K2Unhti/LeC2HPhHo3bt30aZNG3Ts2BF//vknAgMDceHCBVSqVEmMmT59Or755hssWbIEERER+PjjjxEbG4vTp0/D1dXV6jmVVXquBjfTcgEAtdizQ0RkUuGUJlLbdUXms8a2t7hnx9TEgWPGjClTMg+bNm0aqlatikWLFqFFixaIiIhAly5dULNmTQD6D8GsWbMwbtw4PPXUU2jUqBF++uknJCYmYv369VbNxVou3B+vE+ytho+b0s7ZEBERSZ/FPTtDhw6Fr69vsfNgjRw5EitWrMAXX3xhteR+//13xMbG4rnnnsPOnTtRuXJlvPXWW3jttdcA6CcyTEpKQkxMjPgcHx8ftGzZEnv37jV6lFheXh7y8vLE++np+gn+NBqNVQ9rLFxX0XWeTbwHAIgM9JTEIZQltVFK2D7nJ/U2Sr19BQUFAPT/3BZOeyI1hb1XUm1jWdun0+kgCAI0Gk2xMTvmvu9lgoXTHm/cuBEDBgzAhg0b0LZtWwDAO++8g7Vr12Lbtm2oW7euJaszqXA31KhRo/Dcc8/h4MGDePfddzF//nwMHDgQe/bsQZs2bZCYmGgwSrtv376QyWRYuXJlieudOHEiJk2aVGz5smXLbL5feN0VOXbclCM6RIenI6T3piYisiYXFxeEhISgatWqUKmcZ16yosMtSvLBBx/gww8/LPX6r127hsaNG2PXrl1o2LBhqddjD4sXL8bq1atx4sQJZGRk4MqVK/Dx8TEan5+fj+vXryMpKUksfgtlZ2fjhRdeQFpaGry9jU/Sa3HPTo8ePTB37lz06tULW7duxY8//ojffvsNcXFxqF27tqWrM0mn06F58+b47LPPAABNmzZFfHy8WOyU1tixYzFq1Cjxfnp6OqpWrYouXbqY/GNZSqPRYOvWrejcuTOUSv0uq1+XHAZwB51bNkD35lWs9lr2UlIbpYTtc35Sb6PU25eZmYnLly/Dw8NDPDLHGfz333/i7VWrVmHChAk4c+aMuMzT0xOenvqDVARBQEZGBry8vMwen1L4XA8PD6v+blmTRqOBUqks1j5BENCjRw/06NED//d//wcvLy+TbcjNzYWbmxvat29fbCxu4Z6ZRynVAOUXXngB9+7dQ5s2bRAYGIidO3ciMjKyNKsyKTQ0FPXq1TNYFhUVhTVr1gDQn6cL0E82VbRnJzk5GU2aNDG6XrVaDbVaXWy5Uqm0yZdF0fVeTMkCAESF+Ujqi8lWfztHwfY5P6m3Uartc3HR/0zJZDKnOiw7LCxMvO3r6wuZTCYuu3TpEoYOHYp9+/YhKysLUVFR+Oijj9CrVy+xjTKZDOvWrTM4+MfX1xezZs3CK6+8Io5dfeyxxwAA0dHR2LFjB3Q6HaZMmYIFCxbg1q1biIqKwueff46uXbsCAK5cuYKIiAisXLkS3377LQ4dOoQGDRpg6dKlSEtLw9ChQ3H27Fm0a9cOP/30EwIDA8XX/+GHHzBz5kwkJCSgevXqGD58ON566y2D9a5YsQJz587F/v37MX/+fLzyyivirqvCbThy5EgAwI4dOwAUn6z4YXK5HDKZrMT3uLnvebOKnaK9IEUFBgaiWbNmmDt3rrjsyy+/NOuFzdGmTRucO3fOYNn58+cRHh4OAIiIiEBISAi2bdsmFjfp6enYv38/hg4darU8rCUtR4OkdP2RWJFBPBKLiKg0BEFAjqb853RzUyqscmRQZmYmunfvjk8//RRqtRpLlixB//79cebMGVSvXt2sdRw4cAAtWrTA33//jfr164u7+L7++mvMnDkT3333HZo2bYqFCxeiV69eOHXqFGrVqiU+f8KECZg1axaqVauGwYMH44UXXoCXlxe+/vpruLu7o2/fvhg/fjzmzZsHAFi6dCnGjx+P2bNno2nTpjh69Chee+01eHh4GOxp+fDDDzFz5kw0bdrUoY6INqvYOXr0aInLIyMjkZ6eLj5u7UMDR44cidatW+Ozzz5D3759ceDAASxYsAALFiwQX2/EiBGYMmUKatWqJR56HhYWZpND4cuqcH6dEG9XHolFRFRKORot6o3fUu6ve3pyLNxVZZ+xpXHjxmjcuLF4f/LkyVizZg3++OMPvPPOO2ato7DHxd/fX9zLAQAzZszABx98IB6gM23aNMTFxWHWrFmYM2eOGDd69GjExsYCAN599130798f27ZtQ5s2bQAAQ4YMweLFi8X4CRMmYObMmXj66acB6DsbTp8+je+++86g2BkxYoQY40jM2mpxcXG2zqNEjz/+ONatW4exY8di8uTJiIiIwKxZszBgwAAx5v3330dWVhZef/113Lt3D23btsXmzZsdqqIsdOl+sRPJyQSJiCqszMxMTJw4ERs3bsTNmzdRUFCAnJwcXLt2rUzrTU9PR2JioliwFGrTpg2OHz9usKxRo0bi7eDgYAAwGOgcHBwsnqYhKysLly5dwpAhQ8SjoQH9kXIPDyxu3rx5mdpgKw5/bqwnn3wSTz75pNHHZTIZJk+ejMmTJ5djVqVz6ba+2KkZ6GHnTIiInJebUoHTk2Pt8rrWMHr0aGzduhUzZsxAZGQk1Go1nnnmGeTn54sxhQN5i7Lm9AJFx7oU7pV5eFnhWJvMTP1v1/fff4+WLVsarOfhQ8E9PBzz981qxc7cuXNx+/ZtjB8/3lqrlJyEW/rByREBjvlmICJyBjKZzCq7k+xl9+7deOWVV9CnTx8A+h6Zh3t1AgMDcfPmTfH+hQsXkJ2dLd4vHKNT9HyU3t7eCAsLw+7duxEdHW3wei1atCh1vsHBwQgLC8Ply5cN9qw4E6u9W9asWYOEhAQWOyZcvq0vdmoEcjcWEVFFVatWLaxduxY9e/aETCbDuHHjivXidOrUCbNnz0arVq2g1WrxwQcfGPS8BAUFwc3NDZs3b0aVKlXg6uoKHx8fjBkzBhMmTEDNmjXRpEkTLFq0CMeOHcPSpUvLlPOkSZMwfPhw+Pj4oGvXrsjLy8OhQ4dw9+5dowcxGZOUlISkpCRcvHgRAHDy5El4eXmhWrVq8PPzK1OexljtOL5t27bh8uXL1lqd5Gh1Aq7eYc8OEVFF9+WXX6JSpUpo3bo1evbsidjYWIMxNAAwc+ZMVK1aFe3atcMLL7yA0aNHG0x66+Ligm+++QbfffcdwsLC8NRTTwEAhg8fjlGjRuG9995Dw4YNsXnzZvz+++8GR2KVxquvvooffvgBixYtQsOGDREdHY3FixcjIiLC4nXNnz8fTZs2Fcf/tG/fHk2bNsXvv/9ephxNsXgGZSlKT0+Hj4/PI2dgtJRGo8GmTZvQvXt3JKbnI/qLHVC5yHF2clfI5dI4qV3RNkpxjg+2z/lJvY1Sb19GRgbOnz+PqKgoyZ75XKfTIT09Hd7e3k41l5C5ytq+3NxcJCQkICIiosRJBc35/S71bqzTp0/j2rVrBgOqAKBXr16lXaWkFe7CivD3kEyhQ0RE5AwsLnYuX76MPn364OTJkwajxQtHcxcdLEUPXL5VOF6Hu7CIiIjKk8X9Se+++y4iIiKQkpICd3d3nDp1Crt27ULz5s3FqZ+puMu39IfusdghIiIqXxb37Ozduxfbt29HQECAeD6Ltm3bYurUqRg+fLjR2ZYruoTC3VgBPBKLiIioPFncs6PVauHlpT+vU0BAABITEwEA4eHhxc5jRQ9wNxYREZF9WNyz06BBAxw/fhwRERFo2bIlpk+fDpVKhQULFqBGjRq2yNHpZeUViCcArcHDzomIiMqVxcXOuHHjkJWl76WYPHkynnzySbRr1w7+/v5YuXKl1ROUgit39LNe+nmo4OuusnM2REREFYvFxU7hWVIB/VnPz549i9TUVFSqVMnqZz2XisJih5MJEhERlT+rnC7CVtM7S4V4mggWO0REROXOrAHKb775Jm7cuGHWCleuXFnmc3BIzdXCnh0OTiYiIip3ZhU7gYGBqF+/Prp374558+bh4MGD+O+//3Dnzh1cvHgRv//+O95//31Uq1YNX331FRo2bGjrvJ3K9bs5AIBwPxY7REQVgUwmM3mZOHFimdZ/5coVyGQyHDt2zCr5lpfU1FS88847qFOnDtzc3FCtWjUMHz4caWlpNn1ds3ZjffLJJ3j77bfxww8/YO7cuTh9+rTB415eXoiJicGCBQvQtWtXmyTqzK6l6nt2qvlJ87wuRERk6ObNm+LtlStXYvz48QbTs3h6Sn/ONY1GU+x8bYmJiUhMTMSMGTNQr149XL16FW+++SYSExOxevVqm+Vi9jw7wcHB+Oijj3Dy5Encvn0bR44cwe7du3Hu3DncvXsXq1evZqFTgjwtcDtTf/6wav4sdoiIKoKQkBDx4uPjA5lMJt7PysrCgAEDEBwcDE9PT7Rs2bLYGQhkMhnWr19vsMzX1xeLFy8GAPFs402bNoVMJkOHDh0A6E+6OXnyZFSpUgVqtRpNmjTB5s2bxXUU9gitWrUK7dq1g5ubGx5//HGcP38eBw8eRPPmzeHp6Ylu3brh1q1bBq//ww8/ICoqCq6urqhbty7mzp1bbL0rV65EdHQ0XF1dSxzS0qBBA6xZswY9e/ZEzZo10alTJ3z66af4448/UFBQUMq/9qOVaoBypUqVUKlSJWvnIkl39NPrwNddCR836Z2RmIio3AkCoMku/9dVugNWOOo4MzMT3bt3x6effgq1Wo0lS5agf//+OHPmDKpXr27WOg4cOIAWLVrg77//Rv369aFS6ac1+frrrzFz5kx89913aNq0KRYuXIhevXrh1KlTqFWrlvj8CRMmYNasWahWrRoGDx6MF154AV5eXvj666/h7u6Ovn37Yvz48Zg3bx4AYOnSpRg/fjxmz56Npk2b4ujRo3jttdfg4eGBgQMHiuv98MMPMXPmTDRt2rTYGcqNKTxjuYuLVY6ZKpHt1kwAgNt5+g8Gd2EREVmJJhv4LKz8X/f/EgFV2cdeNm7cGI0bNxbvT548GWvWrMEff/yBd955x6x1BAYGAgD8/f0REhIiLp8xYwY++OAD9OvXDwAwbdo0xMXFYdasWZgzZ44YN3r0aHEqmXfffRf9+/fHtm3b0KZNGwDAkCFDxF4kQF8czZw5E08//TQAfc/S6dOn8d133xkUOyNGjBBjzHH79m188skneP31181+Tmmw2LGxwp4dFjtERAToe3YmTpyIjRs34ubNmygoKEBOTg6uXbtWpvWmp6cjMTFRLFgKtWnTBsePHzdY1qhRI/F2cHAwABgcXBQcHIyUlBQAQFZWFi5duoQhQ4bgtddeE2MKCgrg4+NjsN7mzZtblG+PHj1Qr169Mg/YfhQWOzZ2O5c9O0REVqV01/ey2ON1rWD06NHYunUrZsyYgcjISKjVajzzzDPIz88XY2QyGQRBMHieRqOxyusDMBg4XDgh8MPLdDodAH1xBgDff/89WrZsabAehUJhcN/Dw7yer4yMDHTt2hVeXl5Yt25dsYHM1mZRsSMIAq5fv46goCCz98VVdLfv9+yEc3AyEZF1yGRW2Z1kL7t378Yrr7yCPn36AND3cDzcqxMYGGhwRNeFCxeQnf1gnFLhGB2tVisu8/b2RlhYGHbv3o3o6GiD12vRokWp8w0ODkZYWBguX76MAQMGlHo9hdLT0xEbGwu1Wo3ff/+9XOoJi4udyMjIYgOdyLg74pgd5/1gEhGR9dSqVQtr165Fz549IZPJMG7cuGK9OJ06dcLs2bPRqlUraLVafPDBBwa9H0FBQXBzc8PmzZtRpUoVuLq6wsfHB2PGjMGECRNQs2ZNNGnSBIsWLcKxY8fKPNnvpEmTMHz4cPj4+KBr167Iy8vDoUOHcPfuXYwaNcrs9aSnp6NLly7Izs7GL7/8gvT0dKSnpwPQF3gP9xRZi9mHngOAXC5HrVq1cOfOHZskIzVanYDUPP1tHnZOREQA8OWXX6JSpUpo3bo1evbsidjYWIMxNAAwc+ZMVK1aFe3atcMLL7yA0aNHw939we+Ii4sLvvnmG3z33XcICwvDU089BQAYPnw4Ro0ahffeew8NGzbE5s2b8fvvv5e5g+LVV1/FDz/8gEWLFqFhw4aIjo7G4sWLxUPgzXXkyBHs378fJ0+eRGRkJEJDQ8XL9evXy5SjKTLh4XLyEf744w9Mnz4d8+bNQ4MGDWyVV7lKT0+Hj4+PePibtVy5lY4OM/+BUiHD2U+6QSGX3olSNRoNNm3ahO7du9t8n6s9sH3OT+ptlHr7MjIycP78eURFRRn82EuJTqdDeno6vL29IZdb1AfhFMravtzcXCQkJCAiIqLYLi9zf78tHqD88ssvIzs7G40bN4ZKpYKbm5vB46mpqZauUrIKZ06uWslNkoUOERGRM7C42Jk1a5YN0pCm66n6c2JVrSTN/0aIiIicgcXFTtHJg8i0a/eLnWp+bo+IJCIiIlsp1c7BS5cuYdy4cejfv7846dCff/6JU6dOWTU5Z5d0+w5qy64j3JfTGREREdmLxcXOzp070bBhQ+zfvx9r164VJxs6fvw4JkyYYPUEndnEKy/iL/UHiFL8Z+9UiIiIKiyLi50PP/wQU6ZMwdatW8VJjQD9nAD79u2zanLOLkmun4K7muzWIyKJiIjIViwudk6ePCnO+lhUUFAQbt++bZWkpKJOlP48IyG6m4+IJCIiIluxuNjx9fU1mMK60NGjR1G5cmWrJCUVgm84AEB+74p9EyEiIqrALC52+vXrhw8++ABJSUniicJ2796N0aNH4+WXX7ZFjk5LqKSfWVJ276qdMyEiIqq4LC52PvvsM9StWxdVq1ZFZmYm6tWrh/bt26N169YYN26cLXJ0Xvd7dmR3r9g3DyIiogrM4mJHpVLh+++/x6VLl7Bhwwb88ssvOHv2LH7++WebncDLWQmVqutvpN0AtBq75kJEROUrIyMDI0aMQHh4ONzc3NC6dWscPHhQfPyVV16BTCaDQqFApUqVoFAo0LVrV/HxvLw8vPTSS/D29kbt2rXx999/G6z/iy++wDvvvFNu7XFmpZ4Aplq1aqhWrZo1c5EezxBoZUooBA2Qdh3wq2HvjIiIqJy8+uqriI+Px88//4ywsDD88ssviImJwenTp8Uxrl27dsWPP/6IjIwMeHl5GZyCacGCBTh8+DD27t2LP//8Ey+88AKSk5Mhk8mQkJCA77//HocOHbJX85yKxcWOIAhYvXo14uLikJKSAp1OZ/D42rVrrZac05PJkKUOgnfuf0BqAosdIqIKIicnB2vWrMFvv/2G9u3bAwAmTpyIP/74A/PmzcOUKVMAAGq1GiEhIXB3dy92oswzZ86gV69eqF+/PmrUqIExY8bg9u3bCAwMxNChQzFt2jSrnrxayiwudkaMGIHvvvsOHTt2RHBwMGQynuDSlCzV/WKH43aIiKwqKyvL6GMKhcLgDNmmYuVyuUGPSkmxHh4eFuVWUFAArVZb7Czdbm5u+Pfff8X7O3bsQEhICHx8fPDEE0/g008/hb+/PwCgcePG+Pnnn5GTk4MtW7YgNDQUAQEBWLp0KVxdXUucBoZKZnGx8/PPP2Pt2rXo3r27LfKRnGx1oP7G3QT7JkJEJDGenp5GH+vevTs2btwo3g8KCkJ2dnaJsdHR0dixY4d4v3r16sXmjRMEwaLcvLy80KpVK3zyySeIiopCcHAwli9fjr179yIyMhKAfhfW008/jfDwcMTHx+PTTz9Ft27dsHfvXigUCgwePBgnTpxAvXr1EBAQgFWrVuHu3bsYP348duzYgXHjxmHFihWoWbMmFi5cyOlfTLC42PHx8UGNGtwdY64sdZD+RiqLHSKiiuTnn3/G4MGDUblyZSgUCjRr1gz9+/fH4cOHAeincgEAnU6H8PBwtGzZErVq1cKOHTvwxBNPQKlUYs6cOQbrHDRoEIYPH46jR49i/fr1OH78OKZPn47hw4djzZo15d5GZ2FxsTNx4kRMmjQJCxcuNOj2o5JlqfSnjMBdzrVDRGRNhedmLMnDRwcXnrS6JEXHyQDAlStXypRXoZo1a2Lnzp3IyspCeno6QkND8fzzzxvtMKhRowYCAgJw8eJFPPHEE8Uej4uLw6lTp/DDDz9gzJgx6N69Ozw8PNC3b1/Mnj3bKjlLlcXFTt++fbF8+XIEBQWhevXqUCqVBo8fOXLEaslJgcFuLEEAOMaJiMgqLBlHY6tYc9fn4eGBu3fvYsuWLZg+fXqJcTdu3MCdO3cQGhpa7LHc3FwMGzYMS5cuhUKhgFarFXetaTQaaLVaq+YsNRYXOwMHDsThw4fx4osvcoCyGbJVARAggyw/E8i+A3gE2DslIiIqB1u2bIEgCKhTpw4uXryIMWPGoG7duhg0aBAyMzMxadIkPPPMMwgKCsLJkycxefJkREZGIjY2tti6PvnkE3Tv3h1NmzYFALRp0wZjxozBoEGDMHv2bLRp06a8m+dULC52Nm7ciC1btqBt27a2yEdydHIV4BUKZCTqx+2w2CEiqhDS0tIwduxY3LhxA35+fnjmmWfw6aefQqlUoqCgACdOnMCSJUtw7949hISEIDY2FlOmTIFarTZYT3x8PFatWoVjx46Jy5599lns2LED7dq1Q506dbBs2bJybp1zsbjYqVq1Ko/rt5BQqTpkGYn6XVlVH7d3OkREVA769u2Lvn37lviYm5sbtmzZAkA/QDk9Pb3YPDuFGjRogAsXLhgsk8vlmDt3LubOnWv9xCXI4tNFzJw5E++//77VBnBVCPdPCMojsoiIiMqfxT07L774IrKzs1GzZk24u7sXG6CcmppqteSkQiicOfnORfsmQkREVAFZXOzMmjXLBmlIm+Cnn0AKdy6YDiQiIiKrK9XRWGQZwb+m/sadSzz8nIiIqJyV6qznWq0W69evx5kzZwAA9evXR69evYpN4kT3VYoAIAPy0oHMFMAr2N4ZERERVRgWFzsXL15E9+7d8d9//6FOnToAgKlTp6Jq1arYuHEjatasafUknZ6LGvCtBty7qh+3w2KHiIio3Fh8NNbw4cNRs2ZNXL9+HUeOHMGRI0dw7do1REREYPjw4bbIURoCaumvOW6HiIioXFncs7Nz507s27cPfn5+4jJ/f398/vnnnMHRFP9I4OLfPCKLiIionFncs6NWq5GRkVFseWZmJlQqlVWSkiT/+0dk3WaxQ0REVJ4sLnaefPJJvP7669i/fz8EQYAgCNi3bx/efPNN9OrVyxY5SgN3YxEREdmFxcXON998g5o1a6JVq1ZwdXWFq6sr2rRpg8jISM7BY0phz87dK4BWY9dUiIjI9iZOnAiZTGZwqVu3rvj4qFGj4Ofnh/DwcKxatcrgub/++it69uxZ3ilLlsVjdnx9ffHbb7/h4sWL4qHnUVFRiIyMtHpykuIVBijdAU02cPcqEMC/FxGR1NWvXx9///23eN/FRf+z+8cff2DZsmX466+/cO7cObz66qvo3bs3goKCkJaWho8++sjgeVQ2Fhc7kydPxujRoxEZGWlQ4OTk5OCLL77A+PHjrZqgZMjlgF9NIPmkfpAyix0iojLJysoy+phCoYCrq6tZsXK5HG5ubiZjPTw8SpWji4sLQkJCii0/c+YMOnTogObNm6NZs2YYOXIkEhISEBQUhPfffx9Dhw5FtWrVSvWaVJzFu7EmTZqEzMzMYsuzs7MxadIkqyQlWQE8bQQRkbV4enoavTzzzDMGsUFBQUZju3XrZhBbvXr1YjGldeHCBYSFhaFGjRoYMGAArl27BgBo3LgxDh06hLt37+Lw4cPIzc1FZGQk/v33Xxw5coRTuViZxcWOIAiQlXC6g+PHjxscjk4lKBy3w8PPiYgkr2XLlli8eDE2b96MefPmISEhAe3atUNGRgZiY2Px4osv4vHHH8fgwYMxd+5ceHh4YOjQoZg/fz7mzZuHOnXqoE2bNjh16pS9m+L0zN6NValSJXGAVe3atQ0KHq1Wi8zMTLz55ps2SVIy/O8fkXWbPTtERGVV0l6GQg+fviglJcVorFxu+H//lStXypRXoaI9Ro0aNULLli3FwchDhgzBxIkTMXHiROh0OqSnp+Pzzz9HTEwMlEolpkyZgpMnT2LDhg14+eWXcfjwYavkVFGZXezMmjULgiBg8ODBmDRpEnx8fMTHVCoVqlevjlatWtkkSckIrK2/vnXWvnkQEUmAJeNobBVrCV9fX9SuXRsXLxbv3T9//jyWLl2Ko0ePYuHChWjfvj0CAwPRt29fDB48GBkZGfDy8rJJXhWB2cVO4dnOIyIi0Lp1ayiVSpslZcznn3+OsWPH4t133xUPc8/NzcV7772HFStWIC8vD7GxsZg7dy6Cgx3w/FMBdQDIgOw7QOYtwDPQ3hkREVE5yczMxKVLl/DSSy8ZLBcEASNHjsSMGTPg6ekJrVYLjUY/RUnhtVarLfd8pcTiMTsRERG4efMmrl27VuLFVg4ePIjvvvsOjRo1Mlg+cuRI/PHHH/j111+xc+dOJCYm4umnn7ZZHmWicgcqhetv3zpj31yIiMimRo8ejZ07d+LKlSvYs2cP+vTpA4VCgf79+xvE/fDDDwgICBDn1WnTpg22b9+Offv24auvvkK9evXg6+trhxZIh8WHnlevXr3EAcqFbFF9ZmZmYsCAAfj+++8xZcoUcXlaWhp+/PFHLFu2DJ06dQIALFq0CFFRUdi3bx/+97//WT2XMguM0k8seOscENHe3tkQEZGN3LhxA/3798edO3cQGBiItm3bYt++fQgMfNCrn5ycjKlTp+LPP/8Ul7Vo0QLvvfceevTogaCgICxZssQe6UuKxcXO0aNHDe5rNBocPXoUX375JT799FOrJVbUsGHD0KNHD8TExBgUO4cPH4ZGo0FMTIy4rG7duqhWrRr27t1rtNjJy8tDXl6eeD89PV1sS2GXoTU83A0JAHL/WlDgT2iTTkFnxdeyl5LaKCVsn/OTehul3r6CggIA+l09Op3OztlYZtmyZSUuL9qOwMBAXLp0CRkZGQZtHDduHMaNG1fic5yNIAjidWnaodPpIAgCNBpNsYHn5r7vLS52GjduXGxZ8+bNERYWhi+++MLqu5BWrFiBI0eO4ODBg8UeS0pKgkqlKta9FxwcjKSkJKPrnDp1aolzAv31119wd3cvc84P27p1q3i7SmoeHgNw9/we7BY2Wf217KVoG6WI7XN+Um+jVNtXOClfVlaWZAu6QiWdZFtKStu+/Px85OTkYNeuXWLxWyg7O9usdVhc7BhTp06dEguSsrh+/TreffddbN261WAmzLIaO3YsRo0aJd5PT09H1apV0aVLF3h7e1vtdTQaDbZu3YrOnTs/GNB9szKw8Dv4a2+he7dugIldgs6gxDZKCNvn/KTeRqm3LzMzE5cvX4aHh4fBLMdSIgiCeLSVqWEizqqs7cvNzYWbmxvat29frBYo3DPzKBYXOw+vWBAE3Lx5ExMnTkStWrUsXZ1Jhw8fRkpKCpo1ayYu02q12LVrF2bPno0tW7YgPz8f9+7dM+jdSU5OLnF67kJqtRpqtbrYcqVSaZMvC4P1htQDIIMsJxXK/DTJHJFlq7+do2D7nJ/U2yjV9hWeS0omkxWbD0cqCnftSLWNZW2fXC6HTCYr8T1u7nu+VCcCfbgyEwQBVatWxYoVKyxdnUlPPPEETp48abBs0KBBqFu3Lj744ANUrVoVSqUS27ZtE6cGP3fuHK5du+a4c/4UHpF194r+iCyJFDtERESOyuJiJy4uzuC+XC5HYGAgIiMjxQrcWry8vNCgQQODZR4eHvD39xeXDxkyBKNGjYKfnx+8vb3xzjvvoFWrVo55JFahwiOyUs7yiCwiIhMK/7kuHORKFY81tr3F1Ul0dHSZX9SavvrqK8jlcjzzzDMGkwo6tKC6wPk/OdcOEdEjuLi4QKfTITs722YzG5NjKxyEXJbdtKXuijl9+jSuXbuG/Px8g+W9evUqdTLm2LFjh8F9V1dXzJkzB3PmzLHp61pVYF39dQpPG0FEZIpCoUBGRgZu3boFuVwOd3d3yQ3i1el0yM/PR25urmTH7JSmfYIgIDs7GykpKfD19S122LklLC52Ll++jD59+uDkyZOQyWRi91Lhm49TWpuhsNi5dQYQBKc/IouIyJYyMjJQu3ZtkyfzdGaCICAnJwdubm6SK+SAsrfP19fX5EFH5rC42Hn33XcRERGBbdu2ISIiAgcOHMCdO3fw3nvvYcaMGWVKpsIIrAPI5EDOXSAjCfAOtXdGREQOLTg4GKGhoZKca0ej0WDXrl1o3769JI+oK0v7lEplmXp0Cllc7Ozduxfbt29HQEAA5HI55HI52rZti6lTp2L48OHFZlimEijdAP9awO1zQHI8ix0iIjMoFAqr/PA5GoVCgYKCAri6ukqy2HGE9lm8c1Cr1YqnmQ8ICEBiYiIAIDw8HOfOnbNudlIWcv8os6STpuOIiIioTCzu2WnQoAGOHz+OiIgItGzZEtOnT4dKpcKCBQtQo0YNW+QoTSENgfg1LHaIiIhszOJiZ9y4ccjKygIATJ48GU8++STatWsHf39/q08qKGnBDfXXyfH2zYOIiEjiLC52YmNjxduRkZE4e/YsUlNTUalSJUmOIreZkPvFzp2LQH62fmZlIiIisjqLx+wMHjy42JlL/fz8kJ2djcGDB1stMcnzCgY8AgFBB6RwckEiIiJbsbjYWbJkCXJycootz8nJwU8//WSVpCqMwt6dpBP2zYOIiEjCzN6NlZ6eDkEQxFO1Fz3NularxaZNmxAUFGSTJCUruAFwaTvH7RAREdmQ2cVO4dnOZTIZateuXexxmUyGSZMmWTU5yQtppL9OYrFDRERkK2YXO3FxcRAEAZ06dcKaNWvg5+cnPqZSqRAeHo6wsDCbJClZhXPtJMcDOh0gwXOiEBER2ZvZxU7h2c4TEhJQrVo1HnllDf61AIUayM8E7l0B/DhPERERkbVZ3JUQHh7OQsdaFC5AcD397ZvH7ZsLERGRRHG/ib2FNdVf/3fEvnkQERFJFIsdewtrpr9O5AlUiYiIbIHFjr0V9uwkHtMPUiYiIiKrsvh0EUXdvn0b+/fvh1arxeOPP47Q0FBr5VVxBNYFXNyA/Az9qSMCix/WT0RERKVX6p6dNWvWIDIyEpMmTcKECRNQs2ZNLFq0yJq5VQwKFyC0sf52IsftEBERWZvZxU5mZqbB/UmTJuHAgQM4cOAAjh49il9//RUfffSR1ROsECrfH7fDQcpERERWZ3ax89hjj+G3334T77u4uCAlJUW8n5ycDJVKZd3sKgpxkDKLHSIiImsze8zOli1bMGzYMCxevBhz5szB119/jeeffx5arRYFBQWQy+VYvHixDVOVsMJBykknAa0GUCjtmw8REZGEmF3sVK9eHRs3bsTy5csRHR2N4cOH4+LFi7h48SK0Wi3q1q1rcHJQsoBfDUDtA+SlASlngNBG9s6IiIhIMiweoNy/f38cPHgQx48fR4cOHaDT6dCkSRMWOmUhlwNhTfS3uSuLiIjIqiwqdjZt2oSZM2fi0KFD+OGHHzB9+nQMGDAAY8aMQU5Ojq1yrBgqP6a/vnHQvnkQERFJjNnFznvvvYdBgwbh4MGDeOONN/DJJ58gOjoaR44cgaurK5o2bYo///zTlrlKW9WW+uvrB+ybBxERkcSYXewsXrwYmzZtwooVK3Dw4EH8/PPPAACVSoVPPvkEa9euxWeffWazRCWvagv99e3zQHaqfXMhIiKSELOLHQ8PDyQkJAAArl+/XmyMTr169fDPP/9YN7uKxN0PCLg/ezJ7d4iIiKzG7GJn6tSpePnllxEWFobo6Gh88skntsyrYirs3bm+z755EBERSYjZh54PGDAAXbt2xeXLl1GrVi34+vraMK0Kqur/gKO/sGeHiIjIiiw6Eai/vz/8/f1tlQsVDlL+7zBQkA+4cEZqIiKisir1iUDJBgJqAW5+QEGufjZlIiIiKjMWO45EJityCDrH7RAREVkDix1HUzhI+RqLHSIiImtgseNoqrXSX1/bCwiCfXMhIiKSABY7jqZyM8DFDci6Bdw6a+9siIiInB6LHUfjogaq/U9/O2GXfXMhIiKSABY7jiiinf6axQ4REVGZsdhxRNXb66+v7gZ0OvvmQkRE5ORY7DiisCaAyhPIuQskx9s7GyIiIqfGYscRKZQPjsq6wpOrEhERlQWLHUcljtthsUNERFQWLHYcVfX7xc7V3YC2wL65EBEROTEWO44qtDHg6gvkpetPDEpERESlwmLHUckVQM2O+tsX/7ZvLkRERE6MxY4ji+ysv7641b55EBEROTEWO44s8gn9deJRIPOWfXMhIiJyUix2HJlXCBDcUH/7cpx9cyEiInJSLHYcXa0Y/TXH7RAREZUKix1HF1lY7GzjqSOIiIhKgcWOo6vaElB5Adm3gZvH7J0NERGR02Gx4+gUygeHoJ/bZN9ciIiInBCLHWdQ90n99dmN9s2DiIjICbHYcQa1uwAyBZByGrhzyd7ZEBERORUWO87ArRJQva3+Nnt3iIiILMJix1lwVxYREVGpsNhxFnW766+v7wcyU+ybCxERkRNhseMsfKoAYU0BCDwqi4iIyAIsdpxJ4a6sU+vsmwcREZETYbHjTBo8rb9O2AVkJNs3FyIiIifBYseZ+NUAKj8GCDrg9Hp7Z0NEROQUWOw4m4bP6a9PrrZvHkRERE6CxY6zqd8HkMmBGweAu1ftnQ0REZHDc+hiZ+rUqXj88cfh5eWFoKAg9O7dG+fOnTOIyc3NxbBhw+Dv7w9PT08888wzSE6W8HgWr5AHEwzGr7FvLkRERE7AoYudnTt3YtiwYdi3bx+2bt0KjUaDLl26ICsrS4wZOXIk/vjjD/z666/YuXMnEhMT8fTTT9sx63JQuCvrxCpAEOybCxERkYNzsXcCpmzevNng/uLFixEUFITDhw+jffv2SEtLw48//ohly5ahU6dOAIBFixYhKioK+/btw//+9z97pG179Z4CNr0P3DoD/HcYqNLc3hkRERE5LIcudh6WlpYGAPDz8wMAHD58GBqNBjExMWJM3bp1Ua1aNezdu9dosZOXl4e8vDzxfnp6OgBAo9FAo9FYLd/CdVlznQAAhTsUUT0hP7kKukOLoQ1ubN31W8BmbXQQbJ/zk3ob2T7nJ/U22rJ95q5TJgjOsR9Ep9OhV69euHfvHv79918AwLJlyzBo0CCDwgUAWrRogY4dO2LatGklrmvixImYNGlSseXLli2Du7u79ZO3Af+Ms2h78TNo5K7Y0uBbaBVqe6dERERUrrKzs/HCCy8gLS0N3t7eRuOcpmdn2LBhiI+PFwudshg7dixGjRol3k9PT0fVqlXRpUsXk38sS2k0GmzduhWdO3eGUqm02noBAEI3CPOWQ3k3AV2r5UJo3Me66zeTTdvoANg+5yf1NrJ9zk/qbbRl+wr3zDyKUxQ7b7/9NjZs2IBdu3ahSpUq4vKQkBDk5+fj3r178PX1FZcnJycjJCTE6PrUajXU6uI9IUql0iZvNFutF81eArZNhsvxpUDzl62/fgvYrI0Ogu1zflJvI9vn/KTeRlu0z9z1OfTRWIIg4O2338a6deuwfft2REREGDz+2GOPQalUYtu2beKyc+fO4dq1a2jVqlV5p1v+Gr8AyBTA9X1A8ml7Z0NEROSQHLrYGTZsGH755RcsW7YMXl5eSEpKQlJSEnJycgAAPj4+GDJkCEaNGoW4uDgcPnwYgwYNQqtWraR7JFZR3qFA3R762/vn2zcXIiIiB+XQxc68efOQlpaGDh06IDQ0VLysXLlSjPnqq6/w5JNP4plnnkH79u0REhKCtWvX2jHrcva/ofrrE6uA7FT75kJEROSAHHrMjjkHirm6umLOnDmYM2dOOWTkgKq1AkIaAkkngSM/AW1H2DsjIiIih+LQPTtkBpkMaHm/d+fA94C2wL75EBERORgWO1LQ4BnA3R9IvwGc+c3e2RARETkUFjtSoHQFWryuv/3PVzxfFhERUREsdqSixeuAyhNIPgmc32LvbIiIiBwGix2pcPcDHh+iv73rC/buEBER3cdiR0pavQ24uAL/HQISdto7GyIiIofAYkdKPIOAZgP1t+M+Y+8OERERWOxIT7tRgIsbcH0/cO5Pe2dDRERkdyx2pMYr5MGsytsmAzqtffMhIiKyMxY7UtTmXcDVF7h1Bji+wt7ZEBER2RWLHSly8wXavae/vX0KkJdp13SIiIjsicWOVLV4HahUHchIBP6ZYe9siIiI7IbFjlQpXYGun+tv75kN3L5g33yIiIjshMWOlNXpBtSKBXQa4M/3eSg6ERFVSCx2pK7rVEChAi5tB07zJKFERFTxsNiROv+aQJsR+tubxgDZqXZNh4iIqLyx2KkI2o8GAusCWSn6goeIiKgCYbFTEbiogd5zAZkCiF8NnP7d3hkRERGVGxY7FUXlx/STDQLAhpFA5i375kNERFROWOxUJB0+BILqAdm3gbWvATqdvTMiIiKyORY7FYmLGnh2of5EoZfjgH9m2jsjIiIim2OxU9EERQE97hc5Oz4DLu+wazpERES2xmKnImo6AGgyABB0wKqBwO2L9s6IiIjIZljsVFQ9vgSqPA7k3gOWPcf5d4iISLJY7FRUSleg3zLApxqQehlY+RJQkGfvrIiIiKyOxU5F5hkEvLASUHkBV/8Ffh0EaDX2zoqIiMiqWOxUdMH1gH5LAYUaOLcRWPcGoNPaOysiIiKrYbFDQI1o4PmfAbkSiF8D/P4OCx4iIpIMFjukVzsWePZHQCYHji0FVg/iGB4iIpIEFjv0QL2ngOeWAAoVcPo3YNnzQF6mvbMiIiIqExY7ZKheL+CFVYDSQz/L8qJuwL3r9s6KiIio1FjsUHE1OwIDfwfcA4CkE8D3HYFr++ydFRERUamw2KGSVWkOvB4HBDcEsm4Bi58E9s7hyUOJiMjpsNgh43yrAUO2APV6AzoNsOX/gKXPAhnJ9s6MiIjIbCx2yDSVB/DcYv3pJVxcgUvbgLn/A44tAwTB3tkRERE9EosdejSZDHh8CPD6Tv1urZxUYP1QYElP4M4Fe2dHRERkEosdMl9QXf04nphJgIsbcOUfuCxoj/o3lgI5d+2dHRERUYlY7JBlFEqg7Qhg2D6gVixkOg0ib22By/ftgUtx3LVFREQOh8UOlU6l6sCAVSjo/yuyVEGQZdwEfu6tH89z4HsgN93eGRIREQFgsUNlJNToiH9qj4O22Sv6iQhvnQU2jQa+jAL+GKGfn4e9PUREZEcsdqjM8pS+0HWbAbx3Bug2HQioDeRnAocXAQtjgW+aAHGfAXcu2TtVIiKqgFzsnQBJiKsP0PINoMXrQMIu4PgK4MzvwN0rwM5p+ktQfaBON6BudyC0KSBnvU1ERLbFYoesTyYDakTrLz1mAGc3ASdWApe2Aymn9Jd/ZgCeIUCtzkBEe6B6O8A71N6ZExGRBLHYIdtSeQCNntNfslOBC1uBcxuBi9uAzCTg6M/6CwD4RwLV2wKVmwNhTYHAuoCCb1EiIiob/pJQ+XH3Axo/r78U5AFX/gEu7wAS/tGfcPTORf3l8GJ9vIsbENIACGmoHwfkXwsIiAR8qnH3FxERmY3FDtmHixqIjNFfACDnHnB1D3BtD5B4DLh5HMhLB24c1F8MnusK+NXQn7vLpwrgU/XBtXcY4BEIKF3Lu0VEROSgWOwUkZWVBYVCUWy5QqGAq6urQZwxcrkcbm5u4v3c3FxkZWVBqVQ+MjY7OxuCkcO0ZTIZ3N3dSxWbk5MDnYmzlXt4eJQqNjc3V7yU1MaHY7VardH1urv7QFa3O1C3O/Ly8lCQnw+kJuiLntvn7vf6XALuJsBdyIEs5TSQchp5BQIKSkpX5QG4B8DNJxByr0DAPQD5Kl9oXDwAtfeDi6sXoPYC1N5w8w2C3M0HkCuQn58PjUYDjUZTYvtcXV3F90phrDFFYzUaDfLz843GqtVquLi4WBxbUFCAvLw8o7EqlUrMv2hsSe0rGqvVapGbm2t0vUqlEiqVyuJYnU6HnJwcq8S6uLhArVYDAARBQHZ2tsHjRdvo5uZmMrYoSz73ZfmOsCS2pM99Yfuys7Ph4+NjMrZQeX5HmPrcmxNb2L6ibcnLy0NBQYHR9bq7u0Mmk5kV6+bmBvn9nuJHfZYtibXkO6Lo746jfUc8Ktacz33httBqtSbzLe13hFkEEtLS0gQARi/du3c3iHd3dzcaGx0dLcbl5+cL3t7eRmObN29usN7w8HCjsfXq1TOIrVevntHY8PBwg9jmzZsbjQ0ICDCIjY6ONhrr7u5uENu9e3eTf7einn32WZOxmZmZYuzAgQNNxqacOyAI5/8ShIM/Cm/1etxkbMK7noIwwVsQJngLo1upTMbGD/XQx04OECY8YXy7ARAOTOstCL+/Kwib3hemv9rJZGzc9x8JwolfBSF+nTB73FCTsRuWfC0IiccE4eZJYdGsKSZjVy1ZIAiZtwQh646w6pdFJmMX/fCdIOTnCIImV9jw2zqTsbO//VbcFnFxcSZjp0+fLsYeOHDAZOyECRPE2Pj4eJOxo0ePFmMTEhJMxr711ltibEpKisnYgQMHirGZmZkmY5999lmD97Cp2NJ+RwiCIAQEBBiNteQ7IioqyiBWat8Rd+/eFWMf+R2RkiLGvvXWWyZjExISxNjRo0ebjI2PjxdjJ0yYYDL2wIEDYuz06dNNxm7dulVYv369kJ+fL8yePdtk7IYNG8T1Llpk+nO/atUqMXbVqlUmYxctWiTGbtiwwWTs7NmzxVhzviPy8/OF9evXC3v27DEZW5rviMLf77S0NMEU9uyQ86lUHQgM1N+uchjAQeOxT84CKimArNtA/K8ADjx6/dp8oMD4fyoA9AOts+//N3bF+H9AAIB/vwJu3P+oHTb+Xw0AYPOHwOX7PUjHHhH7x7vA5dH626eM/9coxl4fo799/hGxm8YAtz/S375i/D9iAMDfE4HcL/RH4N14ROw/XwJTf9TfTn5EDvu/A6au1N+++4j1HvkJ+PwPADIg03gvAgDg5Gpg2g797XzjvRMAgHObgGkRpmMKXY4DptfQ5wAAGuP/keL6fuCLyAf3c1KNxyadBL6o9eB++n9GQ2Wplwxj71wzvt70/wxjk64bj81JNYy9fsN4rCbHMPZyovFYwPDvcC7JZKjLnGaA6v5YvfgU0+ud3QLwvP/5PHrLdOx30YDf/c/cgdumY3/sCoTc703YbWK7AcBPvYG4+719O++ZDFX8+jK6VpXD5Zwa2JNmer2rXwVO3e+VO/SImep/extI+EB/+4TxHkQA+s99ymT97TPGezwBAFsnAFkz9bcvmXivA8COqXAR5qFrfj6OPD7LdKwNyQSB09ump6fDx8cHiYmJ8Pb2LvZ4abuoNRoN1q5di9jYWEnvxtqyZUuJbbRsN5b53c4266JWyiHXZAMFOcjPSoMmJwMFuZk4tPcfNG/cAC5CPlCQA2hy4SorgEKXC2jzkZ+bC01+LqAr0BdKWs2Di64ArgotFEIBoNVAk5eLfM39GJ0WEHSAoAUEAdDpoFYIcJHrAEEHjaYA+QXaIo/fvxb0z1PLtXC5/91foBOQZ6ImUCkApUJmcaxWJyDXRKxSAahKEasTBOSYqHcsiXWRA2oXfawgCMi2UqxCDrjejwWArHzjX5WWxMplgJuydLHZGsHohOQyGeBeytgcjQCdiV8CD1XpYnMLBGhN1JSWxLor8eBzb2z3dSli3ZSA/H5svlaAxkS9bEmsqwugkFseq9EKyDcRq3YBXEoR6wjfEbmv7YbW1/g/EKXZjVX4+52Wllbi73ch9uwU4eHhYfADbSrOXK6urvDw8Cix2HlY0QLFmrFFCyprxhbukzanjUWLxUdRq9XiuAprxqpUqkfv41Xp26/yqQIV9AVr5sUsuDfpbrR9qvsXcyjvX6wWKwiAoIOLoIOLTgt9D+/95RDw4NfuwW0XCHC5/7hGU4CtW/9C55gYKF1cisUqIMBD3INjar0CFMAjYh+QAzD3UyQX12vyDwFA36/y8Ho1BRrs2rkL7du3L9LGkmJNv4a5OaCEHB6EFF+HJTm4C4K+UilCU1CAf/75B+3atQOKtM/8bwjA/E+9ZbH6T73sEVFFY4sr2r7C7ae+fzGHJbEqACqZefla8rl/VKymoAA7d+1Cu/vvUcu+I8zL1wXm/+BbEqvAoz/LmoIC/LNrF9r5VYerm3mffLlcbtFv7aOw2CFyZjIZIFMAUOjPSG8pFw00Lp76aQHMKMidkkaDTNcLQEAtabZRo0GG2xUgqJ6E25cABEVJs33A/TZe1s8tJsU2ajTIcLukPwrXTjhZCREREUkaix0iIiKSNBY7REREJGksdoiIiEjSWOwQERGRpLHYISIiIkljsUNERESSxmKHiIiIJI3FDhEREUkaix0iIiKSNBY7REREJGmSKXbmzJmD6tWrw9XVFS1btsSBAwfsnRIRERE5AEkUOytXrsSoUaMwYcIEHDlyBI0bN0ZsbCxSUlLsnRoRERHZmSSKnS+//BKvvfYaBg0ahHr16mH+/Plwd3fHwoUL7Z0aERER2ZmLvRMoq/z8fBw+fBhjx44Vl8nlcsTExGDv3r0lPicvLw95eXni/bS0NABAamoqNBqN1XLTaDTIzs7GnTt3oFQqrbZeRyL1NrJ9zk/qbWT7nJ/U22jL9mVkZAAABEEwGef0xc7t27eh1WoRHBxssDw4OBhnz54t8TlTp07FpEmTii2PiIiwSY5ERERkOxkZGfDx8TH6uNMXO6UxduxYjBo1Sryv0+mQmpoKf39/yGQyq71Oeno6qlatiuvXr8Pb29tq63UkUm8j2+f8pN5Gts/5Sb2NtmyfIAjIyMhAWFiYyTinL3YCAgKgUCiQnJxssDw5ORkhISElPketVkOtVhss8/X1tVWK8Pb2luQbuCipt5Htc35SbyPb5/yk3kZbtc9Uj04hpx+grFKp8Nhjj2Hbtm3iMp1Oh23btqFVq1Z2zIyIiIgcgdP37ADAqFGjMHDgQDRv3hwtWrTArFmzkJWVhUGDBtk7NSIiIrIzSRQ7zz//PG7duoXx48cjKSkJTZo0webNm4sNWi5varUaEyZMKLbLTEqk3ka2z/lJvY1sn/OTehsdoX0y4VHHaxERERE5Macfs0NERERkCosdIiIikjQWO0RERCRpLHaIiIhI0ljsWGjOnDmoXr06XF1d0bJlSxw4cMBk/K+//oq6devC1dUVDRs2xKZNmwweFwQB48ePR2hoKNzc3BATE4MLFy7YsgkmWdK+77//Hu3atUOlSpVQqVIlxMTEFIt/5ZVXIJPJDC5du3a1dTOMsqR9ixcvLpa7q6urQYyjbT/AsjZ26NChWBtlMhl69OghxjjSNty1axd69uyJsLAwyGQyrF+//pHP2bFjB5o1awa1Wo3IyEgsXry4WIyln2tbsbR9a9euRefOnREYGAhvb2+0atUKW7ZsMYiZOHFise1Xt25dG7bCNEvbuGPHjhLfo0lJSQZxzroNS/p8yWQy1K9fX4xxpG04depUPP744/Dy8kJQUBB69+6Nc+fOPfJ59v4tZLFjgZUrV2LUqFGYMGECjhw5gsaNGyM2NhYpKSklxu/Zswf9+/fHkCFDcPToUfTu3Ru9e/dGfHy8GDN9+nR88803mD9/Pvbv3w8PDw/ExsYiNze3vJolsrR9O3bsQP/+/REXF4e9e/eiatWq6NKlC/777z+DuK5du+LmzZviZfny5eXRnGIsbR+gn/GzaO5Xr141eNyRth9geRvXrl1r0L74+HgoFAo899xzBnGOsg2zsrLQuHFjzJkzx6z4hIQE9OjRAx07dsSxY8cwYsQIvPrqqwYFQWneF7Ziaft27dqFzp07Y9OmTTh8+DA6duyInj174ujRowZx9evXN9h+//77ry3SN4ulbSx07tw5gzYEBQWJjznzNvz6668N2nX9+nX4+fkV+ww6yjbcuXMnhg0bhn379mHr1q3QaDTo0qULsrKyjD7HIX4LBTJbixYthGHDhon3tVqtEBYWJkydOrXE+L59+wo9evQwWNayZUvhjTfeEARBEHQ6nRASEiJ88cUX4uP37t0T1Gq1sHz5chu0wDRL2/ewgoICwcvLS1iyZIm4bODAgcJTTz1l7VRLxdL2LVq0SPDx8TG6PkfbfoJQ9m341VdfCV5eXkJmZqa4zJG2YVEAhHXr1pmMef/994X69esbLHv++eeF2NhY8X5Z/2a2Yk77SlKvXj1h0qRJ4v0JEyYIjRs3tl5iVmROG+Pi4gQAwt27d43GSGkbrlu3TpDJZMKVK1fEZY68DVNSUgQAws6dO43GOMJvIXt2zJSfn4/Dhw8jJiZGXCaXyxETE4O9e/eW+Jy9e/caxANAbGysGJ+QkICkpCSDGB8fH7Rs2dLoOm2lNO17WHZ2NjQaDfz8/AyW79ixA0FBQahTpw6GDh2KO3fuWDV3c5S2fZmZmQgPD0fVqlXx1FNP4dSpU+JjjrT9AOtswx9//BH9+vWDh4eHwXJH2Ial8ajPoDX+Zo5Ep9MhIyOj2GfwwoULCAsLQ40aNTBgwABcu3bNThmWXpMmTRAaGorOnTtj9+7d4nKpbcMff/wRMTExCA8PN1juqNswLS0NAIq954pyhN9CFjtmun37NrRabbFZmYODg4vtOy6UlJRkMr7w2pJ12kpp2vewDz74AGFhYQZv2K5du+Knn37Ctm3bMG3aNOzcuRPdunWDVqu1av6PUpr21alTBwsXLsRvv/2GX375BTqdDq1bt8aNGzcAONb2A8q+DQ8cOID4+Hi8+uqrBssdZRuWhrHPYHp6OnJycqzyvnckM2bMQGZmJvr27Ssua9myJRYvXozNmzdj3rx5SEhIQLt27ZCRkWHHTM0XGhqK+fPnY82aNVizZg2qVq2KDh064MiRIwCs893lKBITE/Hnn38W+ww66jbU6XQYMWIE2rRpgwYNGhiNc4TfQkmcLoLs7/PPP8eKFSuwY8cOg0G8/fr1E283bNgQjRo1Qs2aNbFjxw488cQT9kjVbK1atTI4mWzr1q0RFRWF7777Dp988okdM7ONH3/8EQ0bNkSLFi0MljvzNqxIli1bhkmTJuG3334zGM/SrVs38XajRo3QsmVLhIeHY9WqVRgyZIg9UrVInTp1UKdOHfF+69atcenSJXz11Vf4+eef7ZiZ9S1ZsgS+vr7o3bu3wXJH3YbDhg1DfHy8XceAmYs9O2YKCAiAQqFAcnKywfLk5GSEhISU+JyQkBCT8YXXlqzTVkrTvkIzZszA559/jr/++guNGjUyGVujRg0EBATg4sWLZc7ZEmVpXyGlUommTZuKuTvS9gPK1sasrCysWLHCrC9Oe23D0jD2GfT29oabm5tV3heOYMWKFXj11VexatWqYrsLHubr64vatWs7xfYzpkWLFmL+UtmGgiBg4cKFeOmll6BSqUzGOsI2fPvtt7FhwwbExcWhSpUqJmMd4beQxY6ZVCoVHnvsMWzbtk1cptPpsG3bNoP//otq1aqVQTwAbN26VYyPiIhASEiIQUx6ejr2799vdJ22Upr2AfoR9J988gk2b96M5s2bP/J1bty4gTt37iA0NNQqeZurtO0rSqvV4uTJk2LujrT9gLK18ddff0VeXh5efPHFR76OvbZhaTzqM2iN94W9LV++HIMGDcLy5csNpgwwJjMzE5cuXXKK7WfMsWPHxPylsA0B/VFOFy9eNOsfDntuQ0EQ8Pbbb2PdunXYvn07IiIiHvkch/gttMow5wpixYoVglqtFhYvXiycPn1aeP311wVfX18hKSlJEARBeOmll4QPP/xQjN+9e7fg4uIizJgxQzhz5owwYcIEQalUCidPnhRjPv/8c8HX11f47bffhBMnTghPPfWUEBERIeTk5Dh8+z7//HNBpVIJq1evFm7evCleMjIyBEEQhIyMDGH06NHC3r17hYSEBOHvv/8WmjVrJtSqVUvIzc11+PZNmjRJ2LJli3Dp0iXh8OHDQr9+/QRXV1fh1KlTYowjbT9BsLyNhdq2bSs8//zzxZY72jbMyMgQjh49Khw9elQAIHz55ZfC0aNHhatXrwqCIAgffvih8NJLL4nxly9fFtzd3YUxY8YIZ86cEebMmSMoFAph8+bNYsyj/maO3L6lS5cKLi4uwpw5cww+g/fu3RNj3nvvPWHHjh1CQkKCsHv3biEmJkYICAgQUlJSyr19gmB5G7/66ith/fr1woULF4STJ08K7777riCXy4W///5bjHHmbVjoxRdfFFq2bFniOh1pGw4dOlTw8fERduzYYfCey87OFmMc8beQxY6Fvv32W6FatWqCSqUSWrRoIezbt098LDo6Whg4cKBB/KpVq4TatWsLKpVKqF+/vrBx40aDx3U6nfDxxx8LwcHBglqtFp544gnh3Llz5dGUElnSvvDwcAFAscuECRMEQRCE7OxsoUuXLkJgYKCgVCqF8PBw4bXXXrPLF1AhS9o3YsQIMTY4OFjo3r27cOTIEYP1Odr2EwTL36Nnz54VAAh//fVXsXU52jYsPAz54UthmwYOHChER0cXe06TJk0ElUol1KhRQ1i0aFGx9Zr6m5UnS9sXHR1tMl4Q9Ifah4aGCiqVSqhcubLw/PPPCxcvXizfhhVhaRunTZsm1KxZU3B1dRX8/PyEDh06CNu3by+2XmfdhoKgP8zazc1NWLBgQYnrdKRtWFLbABh8rhzxt1B2P3kiIiIiSeKYHSIiIpI0FjtEREQkaSx2iIiISNJY7BAREZGksdghIiIiSWOxQ0RERJLGYoeIiIgkjcUOERERSRqLHSJyOK+88kqxMz+Xp5deegmfffaZWbH9+vXDzJkzbZwREZUFZ1AmonIlk8lMPj5hwgSMHDkSgiDA19e3fJIq4vjx4+jUqROuXr0KT0/PR8bHx8ejffv2SEhIgI+PTzlkSESWYrFDROUqKSlJvL1y5UqMHz8e586dE5d5enqaVWTYyquvvgoXFxfMnz/f7Oc8/vjjeOWVVzBs2DAbZkZEpcXdWERUrkJCQsSLj48PZDKZwTJPT89iu7E6dOiAd955ByNGjEClSpUQHByM77//HllZWRg0aBC8vLwQGRmJP//80+C14uPj0a1bN3h6eiI4OBgvvfQSbt++bTQ3rVaL1atXo2fPngbL586di1q1asHV1RXBwcF49tlnDR7v2bMnVqxYUfY/DhHZBIsdInIKS5YsQUBAAA4cOIB33nkHQ4cOxXPPPYfWrVvjyJEj6NKlC1566SVkZ2cDAO7du4dOnTqhadOmOHToEDZv3ozk5GT07dvX6GucOHECaWlpaN68ubjs0KFDGD58OCZPnoxz585h8+bNaN++vcHzWrRogQMHDiAvL882jSeiMmGxQ0ROoXHjxhg3bhxq1aqFsWPHwtXVFQEBAXjttddQq1YtjB8/Hnfu3MGJEycAALNnz0bTpk3x2WefoW7dumjatCkWLlyIuLg4nD9/vsTXuHr1KhQKBYKCgsRl165dg4eHB5588kmEh4ejadOmGD58uMHzwsLCkJ+fb7CLjogcB4sdInIKjRo1Em8rFAr4+/ujYcOG4rLg4GAAQEpKCgD9QOO4uDhxDJCnpyfq1q0LALh06VKJr5GTkwO1Wm0wiLpz584IDw9HjRo18NJLL2Hp0qVi71EhNzc3ACi2nIgcA4sdInIKSqXS4L5MJjNYVlig6HQ6AEBmZiZ69uyJY8eOGVwuXLhQbDdUoYCAAGRnZyM/P19c5uXlhSNHjmD58uUIDQ3F+PHj0bhxY9y7d0+MSU1NBQAEBgZapa1EZF0sdohIkpo1a4ZTp06hevXqiIyMNLh4eHiU+JwmTZoAAE6fPm2w3MXFBTExMZg+fTpOnDiBK1euYPv27eLj8fHxqFKlCgICAmzWHiIqPRY7RCRJw4YNQ2pqKvr374+DBw/i0qVL2LJlCwYNGgStVlvicwIDA9GsWTP8+++/4rINGzbgm2++wbFjx3D16lX89NNP0Ol0qFOnjhjzzz//oEuXLjZvExGVDosdIpKksLAw7N69G1qtFl26dEHDhg0xYsQI+Pr6Qi43/tX36quvYunSpeJ9X19frF27Fp06dUJUVBTmz5+P5cuXo379+gCA3NxcrF+/Hq+99prN20REpcNJBYmIisjJyUGdOnWwcuVKtGrV6pHx8+bNw7p16/DXX3+VQ3ZEVBrs2SEiKsLNzQ0//fSTyckHi1Iqlfj2229tnBURlQV7doiIiEjS2LNDREREksZih4iIiCSNxQ4RERFJGosdIiIikjQWO0RERCRpLHaIiIhI0ljsEBERkaSx2CEiIiJJY7FDREREkvb/EAZtireBJbcAAAAASUVORK5CYII="]},"metadata":{}}],"source":["plt.plot(t, L1/(L1+L2)*100, label='Tautomer 1')\n","plt.plot(t, L2/(L1+L2)*100, label='Tautomer 2')\n","plt.axhline(95, c='k', linestyle='--', label='95%')\n","plt.axhline(5, c='k', linestyle='--', label='5%')\n","\n","plt.legend()\n","plt.ylabel('% tautomer (a.k.a. f)')\n","plt.xlabel('Time (s)')\n","\n","plt.grid()\n","plt.ylim(0, 100)"],"metadata":{}},{"id":"b80712ce-8a92-46e2-90d9-c94833b2c142","cell_type":"code","execution_count":4,"outputs":[{"output_type":"stream","name":"stdout","text":["Equilibrium fraction of tautomer 1: 0.9523869293511661\nEquilibrium fraction of tautomer 2: 0.04761307064883393\n"]}],"source":["#calculate the fraction of each tautomer in the equilibrated state.\n","\n","# Note: This is the \"f\" value that we will use in the master equation!!\n","# e.g. f1 = fraction of tautomer 1 in the solvated state. \n","\n","f1 = L1[-1]/(L1[-1]+L2[-1])\n","f2 = L2[-1]/(L1[-1]+L2[-1])\n","\n","print('Equilibrium fraction of tautomer 1:', f1)\n","print('Equilibrium fraction of tautomer 2:', f2)"],"metadata":{}},{"id":"756897c5-8eac-41a1-b98f-ada741f93057","cell_type":"markdown","source":["# Now move to a tautomer + protein simulation. \n","To make the protein-binding simulation work, we'll first need to think up some on-rates and off-rates for the complexation of tautomer 1 with protein, and separately the complexation of tautomer 2 with protein. Both of these will be evolving at the same time. \n","\n","I purposely set these on- and off-rates so that tautomer 2, which is the minor tautomer, is much more potent. The point of this is to simulate the question about down-weighting our Kd predictions if the predicted ligand is a minor tautomer. \n","\n","Looking at [the affinity plot on SPRPages](https://www.sprpages.nl/troubleshooting/high-affinity), these rate values are pretty realistic for a real small molecule ligand of interest. \n","\n","Note the printed Ki's after the cell. These are:\n","- 1 µMolar\n","- 5 nanoMolar"],"metadata":{},"attachments":{}},{"id":"48a0916e-6182-4aa1-a4a2-20a3cf0f0458","cell_type":"code","execution_count":5,"outputs":[{"output_type":"stream","name":"stdout","text":["K_i for tautomer 1 (in Molar): 1e-06\nK_i for tautomer 2 (in Molar): 5e-09\n"]}],"source":["# set some protein equilibrium binding constants using on and off rates:\n","# Rate constants\n","\n","#tautomer 1 binding to protein:\n","k_on1 = 1e3 # M^-1 s^-1\n","k_off1 = 1e-3 # s^-1\n","\n","#tautomer 2 binding to protein:\n","k_on2 = 2e5 # M^-1 s^-1\n","k_off2 = 1e-3 # s^-1\n","\n","# So now we can calculate the true equilibrium binding constants. Important step!\n","# these are assocation constants btw. K_eq, not Kd. \n","true_taut1_k_eq = (k_on1/k_off1)\n","true_taut2_k_eq = (k_on2/k_off2)\n","\n","# and so these are the true Kd's (it's just 1/K_eq)\n","true_taut1_kd = 1/true_taut1_k_eq\n","true_taut2_kd = 1/true_taut2_k_eq\n","print('K_i for tautomer 1 (in Molar):', true_taut1_kd)\n","print('K_i for tautomer 2 (in Molar):', true_taut2_kd)\n"],"metadata":{}},{"id":"c807de55-d6fb-4060-a1f3-0bf83103a5cb","cell_type":"markdown","source":["# Run the protein-binding simulation using the pre-equilibrated tautomer mixture. \n","\n","Note that we now have the true values for the association constants (and thus dissociation constants) for the two tautomer species. We also have the 'f' values for the ligands. So we _could_ apply the master equation now. But first I want to get an intuitive feel for things by running another model and plotting the concentrations of free ligand, free protein, and complexes. \n","\n","This is pretty much the same as the tautomer situation, however the ODE equation is a little bit more involved in order to handle two different ligand-protein binding processes at the same time as regeneration of the tautomer populations amongst the unbound fraction!"],"metadata":{},"attachments":{}},{"id":"70b2d8e4-9347-45c0-8431-f803d632ca40","cell_type":"code","execution_count":6,"outputs":[],"source":["# Define the rate equations\n","def rate_equations(y, t, k_on1, k_off1, k_on2, k_off2, k_tau1, k_tau2):\n"," P, L1, L2, PL1, PL2 = y # concs\n"," # rates equations:\n","\n"," # change in conc of protein wrt time\n"," dPdt = -k_on1 * P * L1 + k_off1 * PL1 - k_on2 * P * L2 + k_off2 * PL2\n","\n"," # change in conc of ligand tautomer 1 wrt time:\n"," dL1dt = -k_on1 * P * L1 + k_off1 * PL1 + k_tau2 * L2 - k_tau1 * L1\n","\n"," # change in conc of ligand tautomer 2 wrt time:\n"," dL2dt = -k_on2 * P * L2 + k_off2 * PL2 + k_tau1 * L1 - k_tau2 * L2\n","\n"," # change in conc of protein complexed with ligand tautomer 1:\n"," dPL1dt = k_on1 * P * L1 - k_off1 * PL1\n","\n"," # change in conc of protein complexed with ligand tautomer 2:\n"," dPL2dt = k_on2 * P * L2 - k_off2 * PL2 \n"," \n"," return [dPdt, dL1dt, dL2dt, dPL1dt, dPL2dt]\n"," # whew.\n","\n","# Initial concentrations\n","P0 = 100e-6 # 100 μM of protein. I guess this is much larger than what typically is used in experiment.\n","L1_0 = L1[-1] # take the equilibrated conc of ligand tautomer 1 from the previous simulation\n","L2_0 = L2[-1] # ditto for tautomer 2\n","\n","PL1_0 = 0 # we start with zero concentration of bound protein to tautomer 1`\n","PL2_0 = 0 # ditto for tautomer 2\n","\n","# Initial conditions\n","y0 = [P0, L1_0, L2_0, PL1_0, PL2_0]\n","\n","# Time points for the simulation\n","t = np.linspace(0, 30, 5000) # 30 second simulation. It's equilibrated in about 15s.\n","\n","# Integrate the rate equations\n","y = odeint(rate_equations, y0, t, args=(k_on1, k_off1, k_on2, k_off2, k_tau1, k_tau2))\n","\n","# Extract the concentrations\n","P = y[:, 0]\n","L1 = y[:, 1]\n","L2 = y[:, 2]\n","PL1 = y[:, 3]\n","PL2 = y[:, 4]"],"metadata":{}},{"id":"cffc5710-d307-46cb-95ef-73638f4bd67f","cell_type":"code","execution_count":7,"outputs":[{"output_type":"display_data","data":{"text/plain":["<Figure size 640x480 with 1 Axes>"],"image/png":["iVBORw0KGgoAAAANSUhEUgAAAjcAAAHACAYAAABeV0mSAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjkuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy80BEi2AAAACXBIWXMAAA9hAAAPYQGoP6dpAACpWklEQVR4nOzdd3xT9frA8c9J2qTpbukGyiyl7I2AypCtuH4KV7wsAdcFVMSBV1mKiIgTFRVFcKJy3SACgoMtMqWUVaRAJ9074/z+KA2ki46kKe3z1rzIOTnjybcjT79TUVVVRQghhBCintA4OwAhhBBCCHuS5EYIIYQQ9YokN0IIIYSoVyS5EUIIIUS9IsmNEEIIIeoVSW6EEEIIUa9IciOEEEKIekWSGyGEEELUK5LcCCGEEKJekeRGCCGEEPVKg05ufvvtN0aNGkVYWBiKovDNN9849H7z5s1DURSbR9u2bR16TyGEEKKhadDJTU5ODp07d+bNN9+stXu2b9+e+Ph46+OPP/6otXsLIYQQDYGLswNwphEjRjBixIhyXy8oKOC///0vn332Genp6XTo0IHFixczYMCAat/TxcWFkJCQap8vhBBCiIo16JqbK5k2bRo7duzg888/5+DBg9x5550MHz6c48ePV/uax48fJywsjJYtW3L33Xdz5swZO0YshBBCCEVVVdXZQdQFiqLw9ddfc+uttwJw5swZWrZsyZkzZwgLC7MeN3jwYHr16sXzzz9f5XusX7+e7OxsIiMjiY+PZ/78+Zw7d47Dhw/j5eVlr7cihBBCNGgNulmqIocOHcJsNtOmTRub/QUFBTRq1AiAo0ePEhUVVeF1nnjiCV544QUAmyawTp060bt3b5o1a8YXX3zB5MmT7fwOhBBCiIZJkptyZGdno9Vq2bt3L1qt1uY1T09PAFq2bEl0dHSF1ylOhMri6+tLmzZtOHHiRM0DFkIIIQQgyU25unbtitlsJikpieuuu67MY3Q6XY2GcmdnZ3Py5EnGjRtX7WsIIYQQwlaDTm6ys7Ntak1iY2PZv38//v7+tGnThrvvvpvx48ezdOlSunbtSnJyMps3b6ZTp07ceOONVb7frFmzGDVqFM2aNeP8+fPMnTsXrVbLXXfdZc+3JYQQQjRoDbpD8datWxk4cGCp/RMmTODDDz/EaDTy3HPPsXr1as6dO0dAQADXXHMN8+fPp2PHjlW+37/+9S9+++03Lly4QGBgINdeey0LFy6kVatW9ng7QgghhKCBJzdCCCGEqH9knhshhBBC1CuS3AghhBCiXmlwHYotFgvnz5/Hy8sLRVGcHY4QQgghKkFVVbKysggLC0OjqbhupsElN+fPn6dp06bODkMIIYQQ1RAXF0eTJk0qPKbBJTfFyxzExcXh7e1t12sbjUZ+/vlnhg4diqurq12vXd9IWVWelFXlSVlVnpRV1Uh5VZ6jyiozM5OmTZtWarmiBpfcFDdFeXt7OyS5cXd3x9vbW775r0DKqvKkrCpPyqrypKyqRsqr8hxdVpXpUiIdioUQQghRr0hyI4QQQoh6RZIbIYQQQtQrktwIIYQQol6R5EYIIYQQ9YokN0IIIYSoVyS5EUIIIUS9IsmNEEIIIeoVSW6EEEIIUa84Nbn57bffGDVqFGFhYSiKwjfffHPFc7Zu3Uq3bt3Q6/W0bt2aDz/80OFxCiGEEOLq4dTkJicnh86dO/Pmm29W6vjY2FhuvPFGBg4cyP79+3n44YeZMmUKGzZscHCkQgghhLhaOHVtqREjRjBixIhKH798+XJatGjB0qVLAYiKiuKPP/7glVdeYdiwYY4KUwghaoWqqqgqoKqoABZQUUEFVS16vei4i8eoFL122TEVXftyJqMJc75CbkYhLi6WEsfabFXwWsX3oMJjS+0p//UKrlPmfR3AZDJhzFZIT8zFxaXBLctYJSajCWO2hsyUfBqFOmcdrqvqK7Rjxw4GDx5ss2/YsGE8/PDD5Z5TUFBAQUGBdTszMxMoWtjLaDTaNb7i69n7uvWRlFXl1deysphVzCYLpkIzZqMFk8mCudCCyWjBbLJgMatFD5MFi0XFbLq4bb70mrn4+cXXjEYT6bF6fs2IAVVBNatYVFAtatFDVVEtYCnetlzcVi89Vy8+t5TYtjnv4nVsk4rLko1S2yWSEkC1cPHFihMGx/Lk4y27nHXzq5AnX/y+19lBXCU82HDib+58qrvdrliV34FXVXKTkJBAcHCwzb7g4GAyMzPJy8vDYDCUOmfRokXMnz+/1P6ff/4Zd3d3h8S5ceNGh1y3PpKyqjxnlZVqBotRwWIC1axgMSmolz83c3Ff6eeqpfjfouMv/xf1yiv7Vo+OmH+SHHRtIURlZWdnsW7dOrtdLzc3t9LHXlXJTXXMnj2bmTNnWrczMzNp2rQpQ4cOxdvb2673MhqNbNy4kSFDhjhkmff6RMqq8uxVVhaLSkGOkbwsI3lZheRlGcnPNlKQa6Igz1T078VHYfHzPBNmo+XKFxdCiBI8Pb0YOXKA3a5X3PJSGVdVchMSEkJiYqLNvsTERLy9vcustQHQ6/Xo9fpS+11dXR32oerIa9c3UlaVV15ZWSwqeZmFZKXlk5NWQHZaAdlp+eRmFpKbWUheViG5WUbyswqd2PwhhGhoFEWx6+/3qlzrqkpu+vTpU6qKa+PGjfTp08dJEQnheKpFxZyvcP54OjlpRjKS88hKySM7rYCstHxy0wuxWOpH1qIooNVpcXHRoHFR0GgVtFoNGq2CxkWDVlu0T3Nxn9ZFY7OtaODc+TiaNW+Gq6sLilZBoyn6Jatoih4aDUXPleLtovNKbV88RqMpY79GQVFAQQENKBeDVwBFA6AU/a8UHVf0cvG+i8+LD6vqMRrFWlbFx1vPvbj/UoFe/tS2GdBoMrJp40YGl1EjaHsN2/OUcjdKfi1LvKiU+bTUNZRyD6zgGkU3LD8YOzAajaxfv54RI0bIH2RXcKmsrnVaDE5NbrKzszlx4oR1OzY2lv379+Pv7094eDizZ8/m3LlzrF69GoD777+fZcuW8fjjj3PPPffwyy+/8MUXX/Djjz866y0IYTfGAjNpCTmkni96pCflkpGcR0ZyHmajJz9sOeTsENG4KOj0Lrjqtbi6adG5aXF1K9rW6S89d3XT4qrX4uKqwcVVg9ZVi4vusueuGlx0GrQuGlx0RdtanaYogajBh5TRaGTduhNcO7K1fABdgdYIGh24eUjtaWVoLia0mouJrijf5WXlLE5Nbv78808GDhxo3S7uGzNhwgQ+/PBD4uPjOXPmjPX1Fi1a8OOPP/LII4/w2muv0aRJE1asWCHDwMVVRVVVMlPySPoni5S4bFLjc0g9n03mhfwrDnm1FzcPVwzeOgyerrh5uKJ3d7n4uPjc49JzN3dX9B4u6Nxc0LrIpOZCiLrPqcnNgAEDKpyfoKzZhwcMGMC+ffscGJUQ9pWdlk/i6UySTmeR9E8myWeyKMg12f0+Gq2Cp58eTz83PHz1ePjqcffSYfB2vfivDndvHW6ermi1kqQIIeqvq6rPjRB1naqqZCTlcf5EOuePFz2yLuTb5dpaVw0+gQbrw9PfDS8/Nzz9ixIag6ertT+GEEI0ZJLcCFFD2WkFnDlygbgjqZw7nk5eZmH1L6aAd4AB/1AP/EM98Aky4Omv48+D27np1uHo9Dr7BS6EEPWUJDdCVJHZbCH+eDpn/k7lzJELXDiXU63ruHm6EtTMi0aNPfEP86BRmCe+Ie646rQ2xxmNRrTHVKmVEUKISpLkRohKMBstxEWncvKvJGIPplS5z4zO4EJQMy+CmnkT1LzoX08/fY1GBgkhhCibJDdClMNstnDm71SO70nk9KEUjPnmSp/r7q0jLMLX+vAP9ZCaFyGEqCWS3AhRQnJcFjE7Eji2J4G8rMot1KZ3d6FJW3/C2/kT1sYXn0CD1MoIIYSTSHIjBFCYZ+LozgSO/HGeC+eyK3VOYLgXzTo0Irx9I4Kbe6GR4dVCCFEnSHIjGrTU+BwObz3L0Z0JGAuu0OykQGgrH1p1DaJl10C8/N1qJ0ghhBBVIsmNaHBUVeVsdBp//fwPZ4+mXfH4kJbetOkVQsuugXj4lF6EVQghRN0iyY2d5BWaWbMnjvUnNIyQpZfrJNWicupAMnvX/0PymawKj/X00xN5TQhtrwnFN9i9liIUQghhD5Lc2ImiwKL1MRSYNPyTmktEiEy2VleoFpUTe5PY82MsaQm55R6nKNCiSyAdrm9Mk0g/Gd0khBBXKUlu7MTNVUvLAA+iE7I4mZxDRIivs0Nq8FRVJe5IKju+OUlKXPmdhN08XWl/bRjtr28s/WiEEKIekOTGjloGFiU3p1KqN2OtsJ+kfzLZ/r8TnItJL/cY70AD3Yc1o03vYFxcteUeJ4QQ4uoiyY0dtQwo6ptxOqX8pg/hWHlZhez85iRHtsdDOV2fGjX2oPvw5rTqFijDt4UQoh6S5MaOGvsaADiXbp9VoEXlWSwqf/92jl3fnSp3aQS/EHd639KSll0CZYI9IYSoxyS5saPi5OZ8ep6TI2lYUs5m88vq6HJHQHn66el5UwvaXhMiNTVCCNEASHJjR2G+RZ1Rz2fko6qq1A44mNls4a+f/uHPdaexmEu3QbnotfQc2ZxOA5vgopM+NUII0VBIcmNHYT5uPNHJxJhRQyWxcbCUs9lsXnWk3FFQET2C6Pt/EXj6yaR7QgjR0EhyY0cuWg1hHuDlJsXqKKqqcmjrWbatPYHFVLq2xi/EnevviqRJpJ8TohNCCFEXyKewuGrk5xj5ZXU0sQdSSr2maBS6DQ2n540t0LpKvxohhGjIJLmxs8OpCju/O0L/yCCGdwh1djj1RsKpDDa8d5jstIJSr/mHeXDDhCiCmnk7ITIhhBB1jSQ3dhabpbAp5iw6F60kN3ZyZNt5fv0spsxmqC5Dwrnm5pZSWyOEEMJKkhs789MXfQCfk+HgNWY2W9j21QkObTlb6jWDlys3TGxHs/aNnBCZEEKIukySGzvzvzg4Rybyq5n8HCM/vXuYczFppV5rHOnLkEnt8fCVkVBCCCFKk+TGzqw1N2myBEN1Zafl8/0bB0g9X3qNri5Dwulza0uZjE8IIUS5JLmxs+Kam8x8E1n5RrzcXJ0b0FXmwvlsfnjjQKmOw1oXDQP/HUnkNdKPSQghRMUkubEzvRZ8Da6k5xk5l55H2xBJbior/kQ6P751sNTaUO4+OkY+0Ing5jIaSgghxJVJ3b4DFC/DEC/9birtXEwa372+v1Ri4xvszv893l0SGyGEEJUmNTcO8NbYLvh7GfCWJqlKiTuayro3D2IyWmz2B7fw5qb/dMbNU8pRCCFE5Uly4wCNfQ24usoHcmWcPZrGhnePYC6R2DTv2IihUzvgKgteCiGEqCJJboTTFKRq2bCpdGLTqmsgQ6a0RysjooQQQlSDJDcOEJuSw+pdcRhctfz3xnbODqdOSonLJmWvAdVUIrHpFsSQye0ksRFCCFFt8gniAFn5Jj7eeYbvDpx3dih1UnpiLuvfPoxqUmz2R/QIYqgkNkIIIWpIPkUcoPHF0VJJWQUUlqiZaOiy0wr47rX95GUZbfa36BzA4EntZHI+IYQQNSafJA7g76HDzVWDqkJ8hqwxVcxYYObHtw6QlWo7RL5xG1+GTmkviY0QQgi7kE8TB1AUhTBfAwDn0iS5AVAtKps+PEJKXLbN/oCmnox8oBMurjIqSgghhH1IcuMgjYuTG1kdHICd353i1L5km30u7hZGPNAenUH6tQshhLAfSW4cRJKbS47ujOevn/6x2aczuNCoRy4GL52TohJCCFFfSXLjIMXJTXJWwRWOrN+S47LY+kmMzT5FozBkcltcPVQnRSWEEKI+k/YABxnftzkT+jVv0EswFOQa+endw6Um6et/VxsaR/px4KSTAhNCCFGvSXLjID6GhpvUAKiqyuZV0WQm2zbLdRzQhPbXNcZoNJZzphBCCFEz0iwlHGL/xjhiD6TY7Atu4U2/O1o7KSIhhBANhSQ3DqKqKnO/PczElbtJyW5Y/W4ST2ey8xvbNic3D1eGTe2A1kW+5YQQQjiWNEs5iKIobDySyPmMfOJScwnw1Ds7pFphLDCzaeURLJbLOgsrMGRyO7z83ZwXmBBCiAZD/ox2oLAGOBx821fHSU/MtdnXY0Rzwts1clJEQgghGhpJbhyosV/DmqU49kAyf/9uu1hoUHNvetzY3DkBCSGEaJAkuXGghjSRX152IVs+Pmqzz0WvZcgkWeVbCCFE7ZJPHQcqbpY63wCSmz++OF5qpe/r7ozAN9jdSREJIYRoqCS5caDiZqmz9bxZ6p/DFzi2O9FmX4vOAUT1C3VSREIIIRoySW4cqMnFmpusfJOTI3GcwnwTWz+xbY7Su7vQf2wkiqI4KSohhBANmQwFd6CWgZ4cnDe0Xi/BsPObU2Sn2c7j0/f/WuPh0zCGvgshhKh7pObGgbQapV4nNomxmRz69azNvsaRfkT1leYoIYQQziPJjagW1aLy2+cxcNlcfS6uGgb+u600RwkhhHAqSW4c7Ms/45i0cjdf7T175YOvItE74kn6J8tmX8+bWuATaHBSREIIIUQRSW4c7FRKDltikjl4Nt3ZodhNQa6x1NpRvsHudL6hqZMiEkIIIS6R5MbBwv2L5nk5k5p7hSOvHru/jy09p82YCFkUUwghRJ3g9E+jN998k+bNm+Pm5kbv3r3ZvXt3hce/+uqrREZGYjAYaNq0KY888gj5+fm1FG3VNfUrSm7i6klyc+F8Nod+PWezr0XnAFk7SgghRJ3h1ORmzZo1zJw5k7lz5/LXX3/RuXNnhg0bRlJSUpnHf/rppzz55JPMnTuX6Oho3n//fdasWcNTTz1Vy5FXXnHNTVxanu1K2VepnV+fRL3sfWhdNVx7Z4QTIxJCCCFsOTW5efnll5k6dSqTJk2iXbt2LF++HHd3dz744IMyj9++fTv9+vVj7NixNG/enKFDh3LXXXddsbbHmUJ93dAoUGiykJxdcOUT6rBzMWmcPnTBZl/XIeF4B0gnYiGEEHWH05KbwsJC9u7dy+DBgy8Fo9EwePBgduzYUeY5ffv2Ze/evdZk5tSpU6xbt46RI0fWSszV4arVWNeYupr73aiqyvb/nbDZZ/BypevQcCdFJIQQQpTNaTMUp6SkYDabCQ4OttkfHBzM0aNHyzxn7NixpKSkcO2116KqKiaTifvvv7/CZqmCggIKCi7VmGRmZgJgNBoxGo3lnVYtxdcred0mvm5k5Bm5kJVn93vWlpN/JZca+t19RDiKVq3WeyqvrERpUlaVJ2VVeVJWVSPlVXmOKquqXE9RVdUpHUHOnz9P48aN2b59O3369LHuf/zxx/n111/ZtWtXqXO2bt3Kv/71L5577jl69+7NiRMneOihh5g6dSrPPPNMmfeZN28e8+fPL7X/008/xd29dlasNlrA1eldt6tPtUDCbx6Y8y69CRcPC8HX5qBcxe9LCCHE1SM3N5exY8eSkZGBt7d3hcc6LbkpLCzE3d2dr776iltvvdW6f8KECaSnp/Ptt9+WOue6667jmmuuYcmSJdZ9H3/8Mffeey/Z2dloNKU/acuquWnatCkpKSlXLJyqMhqNbNy4kSFDhuDqWn+WXTjyRzx/rLFtkhoyJYoWnQOqfc36WlaOIGVVeVJWlSdlVTVSXpXnqLLKzMwkICCgUsmN05qldDod3bt3Z/PmzdbkxmKxsHnzZqZNm1bmObm5uaUSGK1WCxT1CSmLXq9Hry+9iKOrq6vDvkEdee3aZjZa2P9znM2+kJbeRHQPscsyC/WprBxNyqrypKwqT8qqaqS8Ks/eZVWVazl1VfCZM2cyYcIEevToQa9evXj11VfJyclh0qRJAIwfP57GjRuzaNEiAEaNGsXLL79M165drc1SzzzzDKNGjbImOXXRufQ8nvnmMHmFZj679xpnh1Ml0TviS6363fuWVrJ+lBBCiDKpqgrOaRSycmpyM2bMGJKTk5kzZw4JCQl06dKFn376ydrJ+MyZMzY1NU8//TSKovD0009z7tw5AgMDGTVqFAsXLnTWW6gUvYuGX44moShQYDKjd6m7idjlzEYLe9efttkXFuFL4za+TolHiMpSLRbUwkJUkwnVbEY1mcD63AxmE6rZAqoF1Wwu+kVsNhfN4aRaLj23mFEtFrA+L2tfZV63XLbPAhT98i+6X/EHQdn7VIvl4jbW/apaeh+q5eKHysV9F+9T3j6L2UzQP2dI2r0HjUa59IFU8v7l7YNL1+WyOC6+YHNMydcve65y+X57Xa+Kx5RxrIptTKqq0iwzgzMr3i/64674awZXLo8yrnfFY2r4HouuV/F7vHS9ahxT1rGXadqsGdx4I87i1OQGYNq0aeU2Q23dutVm28XFhblz5zJ37txaiMx+GnnocNdpyS00cy4tj5aBns4OqVKit58vVWvT86YWUmsjrFRVRS0owJKXh5qXhyUvD0tuHpa83KLtggLUQmNRolH8MBb9ayksRC0otH3t4uuW4ucFFxMUkxFM5ovJyeXPL09aTKgmExEmEyefeNLZRXNV8AUyyxi8IcqmBwpJcHYYV4eGXHPTUCiKQri/O0cTsjiTmntVJDdmo4W9P/1jsy8swpcmkX5OikjYi2qxYMnOxpKVhbn438wsLNlZmLOysGRlFz3PzMKSk1OUsOTlouZeTF4uPtTcXCz5+RdrA+qOClNvV1cUFxcUjQZcXIoSdY0GtBoURQNabdn7NApU9HoZ+9AotudrtKAoRc+5eLyigMLFPxhs96FcPF9RKthXfL7tvqJ4L16zeL9GuXQfRcGiWjh2/ARtIiPRumgvu//FeGxiKrHP+hxrXHD5MVw67vIvilIcA5euVfz8smNtjqngejb3K3W9cu5pcz0uO7fi65nNZnbv3k2v3r1xcXUp+54VxW9zbGWOsff1yimzMo5VLvuaVud6JqORjVu20BHnkeSmljTxK0pu4tLynB1KpcTsSihVa9PrphZOikZUxJKbiyk5GXNaGqa0NMypaZjT04q2U4v+LXotFXNaOpasLIf8VaW4uqK4u6MxGKwPRa9H0elQ9DoUnQ6NTofiWvTc5qG/+Frx4/JjXF1RXF1QtNqihOTiA63W+rz4NbOqsvnXXxk8dCiuBoPtOWWMpmzIjEYjqevW4T9ypHSQrQSj0Uhuehrufa6R8roC1WjEYnDuzPWS3NQS6xpTV8EsxapFZd/GMzb7wiJ8aSy1NrVKtVgwpaSQ988ZPA8eIj0tDfXCBUxJSRgTkzAlFT0s2dnVur6i06Hx8kLr6Vn0r7cXGk8vNF6eaD290Hh5ofH0QGNwR+N+MVkxGEpvu7ujcXMrSjiczGg0YvbyQuvnh1Y+gIRosJz/26iBCPcvymKvhuQm9mAK6Ym2cXYf3sxJ0dRvlpwcCmJPYzwbh/HcOQrPnsV49hzGs2cxnj+PenGOpjAgpYLrKAYDLv7+RR/qfn64+Puh9S16rvW/uM/PD62/P1pv76LEpYwpEoQQoj6Q5KaWNPV3x1PvglZTtzvjqqrKXxts+9o0auxJ03b+ToqofjAlJ1Nw8hQFp05SeCqWwlOnKDh1ClPCFTonajS4BAeTpdcR2CYS15BgXIOCcAkKwiUo+OK/QWg9PWrnjQghxFVAkptaMjAyiEPzhtb5kUbxJzNIjM202dd1aHidj7uuUC0WjGfOkB8dTf6R6KJ/jx7FnFJ+vYvW3x9deDiuTZrg2qQxro0bo2vSpGg7JAQTsG7dOjpK3wghhKgUSW5qiaaO19gU2/ezbV8bT389rXsEOSmaus904QJ5+/eTt28fufv3U3AkGktuGU2PioJr06boW7ZE17Il+lYt0bVoib5lC7S+vhXfRBbqE0KIKpHkRlilxudw+qBtDUOXG8LRamWUSbHCuDhyduwgb+9f5O7fh/GfM6WOUfR69JGRuLVti1u7KNzatkUfGYnGyaMHhBCioZDkpha9vPEYPx2OZ9qgCG7uHObscEo5tOWszbbe3YWofqFOiqZuMKWlkbtzJznbd5CzYwfGs2dLHaOPaI2hS1cMXbti6NgBXYsWdWLkkBBCNFTyG7gWJWcVcCwxmxOJWc4OpZSCXCNHd8bb7Gt/fWN0bg3rW0RVVQqOHSP7l1/I+mUL+YcO2R7g4oKhS2c8evXC0LUbhs6d0Np5dXkhhBA107A+uZysRUDRXDexF+recPDo7fGYCi/NNKtoFDr2b+zEiGqPajaTu+dPsjZtIvuXXzCeP2/zuj4yEo9rrsGjbx/ce/RA4yEjk4QQoi6T5KYWNWtU9KH4z4UcJ0diS7WoHPr1nM2+ll0C8PRzc1JEjqeqKvmHD5P5w49krluHKTnZ+pqi1+PRty+egwbi2b8/rkHSoVoIIa4mktzUouYXk5vYlBxUVa0zw6v/+fsCmcm2y0J0GtjESdE4ljE+nvT//Y+M776z6Qys8fHBa/ANeN1wAx59+kjnXyGEuIpJclOLmjUqapbKyjeRlmvE30Pn5IiKlOxI3KixJ6GtfZ0TjAOoJhPZv/1O+hdfkP3bb9aFHhU3N7wGDcL7ppvwvLYfiq5ufD2EEELUjCQ3tcjNVUuojxvxGfmcvpBTJ5Kb9MRczhxJtdnXaVCTOlOrVBPm9HTSPl9D2uef28wE7N6zJ753/B9egwdL/xkhhKiHJLmpZe3DvPF111Foslz54Frw9x8lOs96uNCmZ7CTorGPwjNnSP1wFelff42aV9TcpvX1xee22/C98070LWV1cyGEqM8kuallKyb0dHYIVmaThZgSw7+j+oTiotM6KaKayY+JIeXNt8jauBFUFQB9VBSNJk7Aa8QINNLsJIQQDYIkNw1Y7IEU8rJsp/Zvd23dm1zwSvKPHStKajZssO7zuP46Gt1zD+69e9eLJjYhhBCVJ8mNk9SF0VLR22ybpEJb++AXcvX0QSk8c4bkV18lc/1PRTU1ioL3iOEEPPAA+ogIZ4cnhBDCSSS5qWXn0/O458M9pOca2fnUDU6LI/NCHmeibTsSXy21NuasLFLeXk7qRx9ZF5X0GjqUgP/8B7fINk6OTgghhLNJclPL/Nx1HE0oWn4hLacQPyeNmIreHg/qpW2dwYVW3er2ZHWq2Uz6l1+S/NrrmNPSAPDo25egx2bhFhXl5OiEEELUFZLc1DKDTkuItxsJmUXDwZ2R3FgsKke323YkbtMrGNc63JE4/8gR4ufMJf/wYQB0LVoQ9MTjePbv7/TmPSGEEHWLJDdO0DzA3ZrcdA33q/X7n41OJTutwGZfu351s0nKkptL8ptvkvrhKjCb0Xh5ETh9On53/QvF1dXZ4QkhhKiDJLlxguaNPNh5KpXTKc5ZQDNmV4LNdmC4F4HhXk6JpSK5e/ZwfvZTGM8WzaDsNXw4wU/NlrWehBBCVEiSGydoHnBpjanaVphv4tT+ZJt9kdeE1HocFVELC0l+YxkXVqwAVcUlNJSQOc/gNXCgs0MTQghxFZDkxglaXkxuTqVk1/q9Y/cnYyq8NDuyolGI6FF3ZiQuOHmSc489RsGRaAB8/u92gmc/hdbz6hmiLoQQwrkkuXGC1kGeRAR50iao9puCSjZJhbfzx927bszcm/Hdd8TPmYuan4/Wx4eQZxfgPXSos8MSQghxlZHkxglaBnqycWb/Wr9vTnoBZ4+m2eyL7O38Jim1sJDEFxaT9umnQNHw7tBFi3ANlr41Qgghqk6Smwbk2J7E4iWXAHB109K8c4DzAgJMiYmce3QWeQcOABDw4IME/OdBFG3dHZYuhBCibpPkxolUVaXAZMHNtXY+yEs2SbXqGujUuW30584R99JSzMnJaLy9abzkRTz7136NlhBCiPpF4+wAGqr3/4ilw9wNvLD+aK3c78K5bC6cte3A3MaJTVI5W7fS9O3lmJOT0UdE0GLtV5LYCCGEsAtJbpzES+9CTqGZk8m1M2LqxN4km20PXz2N29T+BIIAqas/In7GQ2iMRgx9+9Ls00/QNW3qlFiEEELUP9Is5SQtAy8OB092/Fw3qqpy8i/b5KZ19yA0mtpdtkBVVZJffY0L77wDQHqvXrRa9gZad/dajUMIIUT9JsmNk7QM9ATgXHoeeYVmDA7s+5J6Poe0BNvZkFt3r92RSKrFQuKiF0j76CMAGj30EMdCQ2QJBSGEEHYnzVJO4u+hw9e96IPd0TMVnyhRa+Pppye4ubdD73k51Wwm/ulnrIlNyNw5+E2ZDLLgpRBCCAeQ5MaJimcqdmS/G1VVOVmiv02rrkEotdQkpZrNnH9yNhn/+x9oNIQtfgG/u+6qlXsLIYRomCS5caJWF5umHNnvpswmqR610ySlqioJ8+aR+f334OJC41deweeWW2rl3kIIIRou6XPjRD2a+5GWW0jzAMd1qHVWk5SqqiQuWkT6l1+BRkPjl5bgPUyWUhBCCOF4ktw40Zie4YzpGe7QezirSSr51ddIW13UxyZ04UK8hw93+D2FEEIIkOSmXiurSapVLYySSl39kXW4d8jcOfjedqvD7ymEvVksFgoLC50dhsMYjUZcXFzIz8/HbDY7O5w6T8qr8mpSVjqdDo2m5j1mJLlxMlVVSckuxMvNxe7LMJw6kGyz7eGrJ6SFY5uksjZtInHRIgACZ86UzsPiqlRYWEhsbCwWi8XZoTiMqqqEhIQQFxeHIiMXr0jKq/JqUlYajYYWLVqg0+lqFIMkN052y5vbOHg2g48n9+baCPsuYnn6YIrNdsvOAQ5tkso7cIBzj84CVcX3X2NoNHWKw+4lhKOoqkp8fDxarZamTZva5a/IushisZCdnY2np2e9fY/2JOVVedUtK4vFwvnz54mPjyc8PLxGSaQkN04W5OUGZHAiKcuuyU1ORgGJsZk2+1p0DrTb9UsqPHuWuAceRC0owLN/f0Keflr+uhFXJZPJRG5uLmFhYbjX49mzi5vd3Nzc5MO6EqS8Kq8mZRUYGMj58+cxmUy41mCSV/kKOVmb4KLh4MeS7DvXTclaG1c3LWFtfO16j2KWvDzOTpuOOTUVfbsoGr+8FMVF8mZxdSruI1DTanEhRNUV/9zVtF+TJDdO1ibYC4DjiVl2vW7J5KZZ+0ZoXez/5VZVlfhn5lBw9CjaRo1o+uabaDw87H4fIWqb1DwKUfvs9XMnyY2TtQ66WHOTmI2qqna5prHATNzRNJt9LTrbtz9PsbTVq8n84QfQamn8ysu4hoY65D5CCCFEZUly42StgzzRKJCRZyQ5u8Au14yLTsVsvDTKQ9EohLdvZJdrXy5n924SX1wCQPATT+DRq5fd7yGEsA9FUfjmm2+cHQYAzZs359VXX3V2GKIek+TGydxctYT7F3VaPJ5on343sSWGgIdF+OLmYd/Vt01paZx/dBaYzXjfPAq/cf+26/WFEFU3ceJEbr311jJfi4+PZ8SIEbUbUCW9++67DBgwAG9vbxRFIT093dkhiaucJDd1wK1dGzP52hYEeulrfC2LReX0oQs2+1p0sm+TlKqqxM9+ClNyMrpWrQidP1/6JwhRx4WEhKDX1/x3jCPk5uYyfPhwnnrqKWeHIuoJSW7qgIcHt+GZm9pZOxfXRNLpTPKzjTb77N3fJu2jj8jeuhVFp6Pxy0vRGAx2vb4Qwv5KNktt376d6667Dnd3d3r06ME333yDoijs378fKBqtMnnyZFq0aIHBYCAyMpLXXnvN5prFNUUvvfQSoaGhNGrUiP/85z8YjZd+ByUlJTFq1CgMBgMtWrTgk08+KRXbww8/zJNPPsk111zjkPcuGh4Zr1vP/PO3ba2Nf5gH3gH2Sz7yjxwhaclLAAQ98ThukZF2u7YQdVluoanc1zSKYjPDuD2Oddc57tdzZmYmt9xyC4MHD+azzz4jLi6Ohx9+2OYYi8VCkyZN+PLLL2nUqBHbt2/n3nvvJTQ0lNGjR1uP27JlC6GhoWzZsoUTJ04wZswYunTpwtSpU4GiBOj8+fNs2bIFV1dXZsyYQVKS7Zp3QtibJDd1REaukeNJWXRv5lejJp4zf6fabNuzI7GloIBzsx5DNRrxvOEG/MaOtdu1hajr2s3ZUO5rAyMDWTnpUof67s9uIs9Y9jwdvVv4s+a+PtbtaxdvITWn9BpWp1+4sQbRVuzTTz9FURRee+01goKC6NChA+fOnbMmJACurq7Mnz/fut2iRQt27NjBF198YZPc+Pn5sWzZMrRaLW3btuXGG29k8+bNTJ06lWPHjrF+/Xp2795Nz549AXj//feJiopy2HsTAiS5qRMKTGa6PvszFhV2P3UDQd5u1bpOXlYhSf/Yzkoc3t7fHiECkPz66xSeOoU2MIDQ556VfjZCXKViYmLo1KkTbm6Xftf0KmO045tvvskHH3zAmTNnyMvLo7CwkC5dutgc0759e7TaSzVRoaGhHDp0CIDo6GhcXFzo3r279fW2bdvi6+tr3zckRAmS3NQBehctzRp5EJuSw/Gk7GonN3HRqXDZVDkuei1hrXztEmPe/v2krvwQgND5C3Dx87PLdYW4WhxZMKzc1zQlEv29zwyu9LF/PDGwZoE5yOeff86sWbNYunQpffr0wcvLiyVLlrBr1y6b40pOka8oSr1ecFRcHSS5qSMigjyJTcnhWGIW/VpXrwNwySapJpF+aF1r3mfckp/P+dlPgcWCzy034zWobv4yFsKRqtIHxlHH2ktkZCQff/wxBQWX5tbas2ePzTHbtm2jb9++PPjgg9Z9J0+erNJ92rZti8lkYu/evdZmqZiYGBnqLRxORkvVEcUjpY5Vc64b1aJy5ohtZ+LwdvZpkkp+4w0KY2NxCQwkWIZqClGnZWRksH//fptHXFyczTFjx47FYrHw8MMPEx0dzYYNG3jppaKBAsXNzREREfz5559s2LCBY8eO8cwzz5RKgK4kMjKS4cOHc99997Fr1y727t3LlClTMJQYYZmQkMD+/fs5ceIEAIcOHWL//v2kpqaWdVkhrkiSmzoi4uICmtVdYyo5Lou8LNsh4PboTJwfHW1tjgqZPx+tj0+NrymEcJytW7fStWtXm8flHYMBvL29+fbbbzl06BDdunXjv//9L3PmzAGw9sO57777uP322xkzZgy9e/fmwoULNrU4lbVy5UrCwsLo378/t99+O/feey9BQUE2xyxfvpyuXbtaOzRff/31dO3ale+++646RSCE85ObN998k+bNm+Pm5kbv3r3ZvXt3hcenp6fzn//8h9DQUPR6PW3atGHdunW1FK3jRAQV19xkVWuNqTMlhoD7BrvjE1izIeCqxULCvPlgseA1fLg0RwlRx3344YeoqlrqsWLFClRVtZm9uG/fvvzxxx/k5eXx559/YrFYcHV1JTw8HAC9Xs/KlStJT08nLS2Nt956i0WLFlnnwSm+X8klHV599VW2bt1q3Q4JCeGHH34gPz+ff/75h3HjxnH69Gmboefz5s0rM+6JEyfav5BEg+DUPjdr1qxh5syZLF++nN69e/Pqq68ybNgwYmJiSmX2AIWFhQwZMoSgoCC++uorGjduzD///FMvet63DPRAo0BmvomkrAKCq9ipuPQQ8Jo3SaV/9RV5Bw6gcXcnePaTNb6eEKLuWL16NcHBwbRp04ZDhw7xxBNPMHr06FJNRkJcjZya3Lz88stMnTqVSZMmAUVVkz/++CMffPABTz5Z+sP0gw8+IDU1le3bt1t76Ddv3rw2Q3YYN1ct0wa2JtDbDTcX7ZVPuExBnomE2JJDwGvWJGVKTSVp6csABD40A9fg4BpdTwhRtyQmJjJnzhySkpIIDQ3lzjvvZOHChc4OSwi7cFpyU1hYyN69e5k9e7Z1n0ajYfDgwezYsaPMc7777jv69OnDf/7zH7799lsCAwMZO3YsTzzxhM08C5crKCiwGRGQmVmUBBiNRpspwu2h+HrVve70gS1LXasyzkRfQLVcasrSuigENfeo0ftLfHEJlowMdJGReI4eXefKqiGRsqo8e5SV0WhEVVUsFku9HtI8a9Ys7rvvPry8vGzmrKrP77kmirsLFH9viPLVpKwsFguqqmI0Gkt9rlfl59ppyU1KSgpms5ngEjUCwcHBHD16tMxzTp06xS+//MLdd9/NunXrOHHiBA8++CBGo5G5c+eWec6iRYtKdaYD+Pnnn3F3d6/5GynDxo0bHXLd8qQf0QM667aLt5GfN5U/m+qVuMXFEX6xHf3EDYM4/PPPNYywfLVdVlczKavKq0lZubi4EBISQnZ2NoWFpWcOrm+ysqo3iKGhkvKqvOqUVWFhIXl5efz222+YTLZLk+Tm5lb6OlfVPDcWi4WgoCDeffddtFot3bt359y5cyxZsqTc5Gb27NnMnDnTup2ZmUnTpk0ZOnQo3t7edo3PaDSyceNGhgwZUmpiq8ooNFmIScziXHo+w9tXvhnoy/17gUtf9I59W9FtWHiV7w9Fmfa5CRPJB7xuvplBDzxQretcSU3LqiGRsqo8e5RVfn4+cXFxeHp62szgW9+oqkpWVlapmhtRNimvyqtJWeXn52MwGLj++utL/fwVt7xURo2Tm4KCAvR6fZXPCwgIQKvVkpiYaLM/MTGRkJCQMs8JDQ3F1dXVpqoqKiqKhIQECgsL0el0pc7R6/Vlxufq6uqwD4rqXjspJ4/bl+/CRaMwdMEw9JXoe5OTUUBavG0226xdQLXfW+ZPG8jftw/FYCD40ZkO/zB15NehvpGyqryalJXZbEZRFDQaDRqN0weUOkxxc0HxexUVk/KqvJqUlUajQVGUMn+Gq/IzXeWv0Pr165kwYQItW7bE1dUVd3d3vL296d+/PwsXLuT8+fOVuo5Op6N79+5s3rzZus9isbB582b69OlT5jn9+vXjxIkTNm14x44dIzQ0tMzE5moT5uOGt5sLJovKyaScSp1z7liazbarm5agZl7Vur+lsJCkixN5NbrnHulELIQQ4qpU6eTm66+/pk2bNtxzzz24uLjwxBNP8L///Y8NGzawYsUK+vfvz6ZNm2jZsiX3338/ycnJV7zmzJkzee+991i1ahXR0dE88MAD5OTkWEdPjR8/3qbD8QMPPEBqaioPPfQQx44d48cff+T555/nP//5TzXeet2jKAptQ4uayqLjK1f9dvaobXLTOMIXjbZ6f1WkffQxxrNncQkMpNHke6p1DSGEEMLZKt0s9eKLL/LKK68wYsSIMquZRo8eDcC5c+d44403+Pjjj3nkkUcqvOaYMWNITk5mzpw5JCQk0KVLF3766SdrJ+MzZ87Y3Ktp06Zs2LCBRx55hE6dOtG4cWMeeughnnjiicq+jTovKsSL3bGpHE2oXnLTpG315rcxpaWRsnw5AIGPPILGQZ2thRBCCEerdHJT3vDskho3bswLL7xQ6QCmTZvGtGnTynzt8lkui/Xp04edO3dW+vpXmyhrzc2Ve5lnJOeRdSHfZl+TttVbrfvCihVYsrLQR0Xhc+st1bqGEKLuUhSFr7/+2maWYmdp3rw5Dz/8sM0sxULYk/SKqmOKm6UqU3Nz9qjtrMQGL1f8Qz2qfE9jUhJpn3wKQNDDD6FIZzkhrkoTJ04sN3mJj49nxIgRtRtQJaSmpjJ9+nQiIyMxGAyEh4czY8YMMjIynB2auIpVabTUggULKnVc8QJsouoig73QKJCSXUhSVj5BXuUPRT0XU6K/TaQfiqbqQxQvvPMuan4+hi5d8Lj++iqfL4So+8obheps58+f5/z587z00ku0a9eOf/75h/vvv5/z58/z1VdfOTs8cZWqUnIzb948wsLCCAoKKndxR0VRJLmpAYNOy8LbOtLEz4C3W/nD3lRV5eyxdJt9TSKr3iRlPHeOtC++ACDw4Ydl/gYh6qmSzVLbt2/ngQce4Pjx43To0IGnn36a2267jX379tGlSxfMZjP33nsvv/zyCwkJCYSHh/Pggw/y0EMPWa85ceJE0tPTufbaa1m6dCmFhYX861//4tVXX7UO201KSmLy5Mls2rSJkJAQnnvuOZu4OnTowNq1a63brVq1YuHChfz73//GZDLh4nJVTccm6ogqfdeMGDGCX375hR49enDPPfdw0003yXh/B7ir15Un4EtPzCUv03b21MbVSG6S334bjEbcr7kGj2t6V/l8IRqMwgqmZ1C04OpWyWM14Gq48rG6qjcxV1ZmZia33HILgwcP5rPPPiMuLq5U/xeLxUKTJk348ssvadSoEdu3b+fee+8lNDTUOoAEYMuWLYSGhrJlyxZOnDjBmDFj6NKlC1OnTgWKEqDz58+zZcsWXF1dmTFjBklJSRXGl5GRgbe3tyQ2otqq9J3z448/cv78eVatWsVjjz3Gfffdx/jx47nnnnuIjIx0VIyiDOePp9tse/jo8Ams2mq+hf/8Q8bX3wBFi2MKISrwfFj5r0UMhbu/vLS9pDUYy5kqvtm1MOnHS9uvdoTcC6WPm+e4PieffvopiqLw2muvERQURIcOHTh37pw1IYGiCdMuX7qmRYsW7Nixgy+++MImufHz82PZsmVotVratm3LjTfeyObNm5k6dSrHjh1j/fr17N69m549ewLw/vvvExUVVW5sKSkpPPvss9x7770OeOeioahytUtYWBizZ88mJiaGNWvWkJSURM+ePenXrx95eXmOiLHByco38t2B86z4/VS5x8SfsP3FFxbhW+UmpQsrVoDZjMf11+HetWu1YhVCXH1iYmLo1KmTzfT2vXr1KnXcm2++Sffu3QkMDMTT05N3332XM2fO2BzTvn17m1njQ0NDrTUz0dHRuLi40L17d+vrbdu2xdfXt8y4MjMzufHGG2nXrh3z5s2rwTsUDV2N6vx69uzJ6dOnOXLkCPv27cNoNGIwVK32QJSWmW9ixmf7cNEojOvTrMxlGErW3IS29q3SPYwJCaR/8y0AAfc7Zv0oIeqVpyqYfV0p8TP62IkKji3xN+XDh6ofkwN9/vnnzJo1i6VLl9KnTx+8vLxYsmQJu3btsjmu5JT4iqJUa9XsrKwshg8fjpeXF19//bUsNSJqpFodZnbs2MHUqVMJCQnhjTfeYMKECZw/f97uC1E2VGE+bvi5u2KyqMQklJ7vJis1n6xU2/ltwiJ8q3SP1JUri/ra9OiBezeptRHiinQe5T9c3apwrKFyxzpQZGQkhw4doqCgwLpvz549Nsds27aNvn378uCDD9K1a1dat27NyZMnq3Sftm3bYjKZ2Lt3r3VfTEwM6enpNsdlZmYydOhQdDod3333Xb1esFTUjiolNy+++CLt2rXjlltuwdPTk99//509e/bw4IMPllvNKKpOURQ6NPYB4PC50vPdlKy10bu7VGl+G1NaGmlfFPUPaHTffdUPVAhR52RkZLB//36bR1xcnM0xY8eOxWKx8PDDDxMdHc2GDRt46eK6csXN2xEREfz5559s2LCBY8eO8cwzz5RKgK4kMjKS4cOHc99997Fr1y727t3LlClTbGr4ixObnJwc3n//fTIzM0lISCAhIQGz2VzD0hANVZWapZ588knCw8MZPXo0iqLw4Ycflnncyy+/bI/YGrQOjX34/XgKh86V7lQYfyLdZju0tW+V5rdJ++gj1Lw89O2i8Li2X01DFULUIVu3bqVriT50kydPttn29vbm22+/5f7776dbt2507NiROXPmMHbsWGutyX333ce+ffsYM2YMiqJw11138eCDD7J+/foqxbNy5UqmTJlC//79CQ4O5rnnnuOZZ56xvv7XX39Zm7pat25tc25sbCzNmzev0v2EgComN9dffz2KovD333+Xe4zMk2IfHa01N6WTm5I1N1VpkjJnZ5P68ScABNx7n3y9hKhHPvzww3L/6FyxYoXNdt++ffnjjz/w9vZGo9HwySef4OrqSnh40VQUer2elStXsnLlSpvzFi1aZHO/kl599VWb7ZCQEH744QebfePGjbM+HzBgQLnzpglRXVVKbspa60k4RoewouQmJiGLQpMFnUtRC2JeViFpCbZDTMOq0Jk4/auvsGRmomveHK8hg+0WrxDi6rJ69WqCg4Np06YNhw4d4oknnmD06NEyKETUCzJDUh3V1N+Aj8GVjDwjxxKzrH1wSg4Bd9FrCQj3rNQ1VbOZtI8+BsB/0iQUbelRWEKIhiExMZE5c+aQlJREaGgod955JwsXLnR2WELYRaWTmxdeeIEZM2bg7u5+xWN37dpFSkoKN954Y42Ca8gUReHdcd0J8zXQxO/SX1Ilm6RCWnij1VauX3jWL79gPHcOrY8PPjePsme4QoirTPFErMXNUkLUJ5X+jj5y5AjNmjWzdihLTk62vmYymTh48CBvvfUWffv2ZcyYMXh5eTkk4Iakd8tGNPV3t+kXE38y3eaYqvS3SVu1GgDfMWPQSNWzEEKIeqrSNTerV6/mwIEDLFu2jLFjx5KZmYlWq0Wv15ObW9QHpGvXrkyZMoWJEyfKPAUOYCo0kxKXbbMvtJVPpc7NP3KE3D//BBcX/Mbe5YjwhBBCiDqhSn1uOnfuzHvvvcc777zDwYMH+eeff8jLyyMgIIAuXboQEBDgqDgbpHyjmRW/nyI6PotX/9WF5DNZWCyXRhUoCgQ1r9zEiamrPwLAe9gwXENCHBKvEEIIURdUq0OxRqOhS5cudOnSxc7hiMvptBqW/3qK7AIT029oTd4p2wn9/MM80bld+UtoSkkh88eihfr8J4x3SKxCCCFEXSG9yOowjUahfVhRzcyhsxkkxNqOlAppWblam/Qvv0Q1GjF07oyhUye7xymEEELUJZLc1HHWyfzOppNwqmRyc+X+NqrZTNqXRUstSF8bIYQQDYEkN3Vc8fw2x05nkJtRaPNaZZKbnD/+wHQ+Ho2PD17DhjkkRiGEKGnixInceuutDr3Hhx9+WGfWNdy6dSuKopRaFLS+mTdv3lXRJUWSmzquc1NfADLP5djs13u44BN05eHcaWu+AMD31lvQyAg2IeqtiRMnoigKiqKg0+lo3bo1CxYswGQy1fi61UlSXnvttXKXgqgKRVH45ptvynxtzJgxHDt2rMb3cIT8/HwmTpxIx44dcXFxqVIZbtmyhZEjR9KoUSPc3d1p164djz76KOfOnXNcwPWMJDd1XPNG7vi6uxJUYLsGVEgLnyuuC2VMSCD74pIZvqNHOypEIUQdMXz4cOLj4zl+/DiPPvoo8+bNY8mSJWUeW1hYWOZ+e/Hx8XF4rYrBYCAoKMih96gus9mMwWBgxowZDB5c+aVu3nnnHQYPHkxISAhr167lyJEjLF++nIyMDJYuXerAiOsXuyY3b731FgsWLLDnJRs8RVHo3MSXJhbbL1VlOhOnf7UWLBbce/RA36qVo0IUQtQRer2ekJAQmjVrxgMPPMDgwYP57rvvgEs1MAsXLiQsLIyoqCgADh06xKBBgzAYDDRq1Ih7772X7Oyi+bTmzZvHqlWr+Pbbb621QsVrDMbFxTF69Gh8fX3x9/fnlltu4fTp09ZYStb4DBgwgBkzZvD444/j7+9PSEgI8+bNq9H7LatZ6rnnniMoKAgvLy+mTJnCk08+adOMsmfPHoYMGUJAQAA+Pj7079+fv/76y+YaiqKwYsUKbrvtNtzd3YmIiLCWY7F169bRpk0bDAYDAwcOtHnvAB4eHrz99ttMnTqVkEpOv3H27FlmzJjBjBkz+OCDDxgwYADNmzfn+uuvZ8WKFcyZM8d67Nq1a2nfvj16vZ7mzZuXSnyaN2/Oc889x/jx4/H09KRZs2Z89913JCcnc8stt+Dp6UmnTp34888/S5XnN998Q0REBG5ubgwbNoy4uLgK416xYgVRUVG4ubnRtm1b3n77betr99xzD506daKgoAAoSqq7du3K+PGOHblr1+Rm7dq1dqmGFLYW39qRMNV2HajgFhX3t1FNJtK/+goompFYCFE9qqqSa8x1yqOmq2UbDAabGprNmzcTExPDxo0b+e6778jJyWHEiBH4+fmxZ88evvzySzZt2sS0adMAmDVrFqNHj7bWCMXHx9O3b1+MRiPDhg3Dy8uL33//nW3btuHp6cnw4cMrrBFatWoVHh4e7Nq1ixdffJEFCxawcePGGr3Hy33yyScsXLiQxYsXs3fvXsLDw20+aAGysrKYMGECf/zxBzt37iQiIoKRI0eSlZVlc9z8+fMZPXo0Bw8eZOTIkYwbN460tDSgKLG7/fbbGTVqFPv377cmUTX15ZdfUlhYyOOPP17m68WJ3N69exk9ejT/+te/OHToEPPmzeOZZ54p9fn7yiuv0K9fP/bt28eNN97IuHHjGD9+PP/+97/566+/aNWqFePHj7f5PsvNzWXhwoWsXr2abdu2kZ6ezr/+9a9yY/7kk0+YM2cOCxcuJDo6mueff545c+bw2WefAfD666+Tk5NjLZ///ve/pKens2zZshqU1JXZdeHMzZs32/Ny4iI1rRCL+bJfcgoEX2Hyvuw//sCUkIDW1xevYUMdHKEQ9VeeKY/en/Z2yr13jd2Fu+uV1/MrSVVVNm/ezIYNG5g+fbp1v4eHBytWrECn02GxWHjjjTfIz89n9erVeHh4ALBs2TJGjRrF4sWLCQ4OxmAwUFBQYFP78PHHH2OxWFixYoW1eXzlypX4+vqydetWhg4t+3dOp06dmDt3LgAREREsW7aMzZs3M2TIkCq/x7K88cYbTJ48mUmTJgEwZ84cfv75Z2tNFMCgQYNsznn33Xfx9fXl119/5aabbrLunzhxInfdVTTC9Pnnn+f1119n7969NGvWjLfffptWrVpZa0siIyM5dOgQixcvrlH8x48fx9vbm9DQ0AqPe/nll7nhhht45plnAGjTpg1HjhxhyZIlTJw40XrcyJEjue+++4Cisnj77bfp2bMnd955JwBPPPEEffr0ITEx0fr1NRqNLFu2jN69i77nV61aRVRUFLt376ZXr16lYpk7dy5Lly7l9ttvB6BFixb8/fffrFy5kvvuuw9PT08+/vhj+vfvj5eXF6+++ipbtmzB27tyU5lUl/S5uQqUHALeKMwDnaHivDTj628A8LnlZjQ6naNCE0LUIT/88AOenp64ubkxYsQIxowZY9P007FjR3SX/T44duwYnTt3tiY2AP369cNisRATE1PufQ4cOMCJEyfw8vLC09MTT09P/P39yc/P5+TJk+We16nEPFuhoaEkJSUBcP/991uv5enpWdW3DkBMTEypD+CS24mJiUydOpWIiAh8fHzw9vYmOzubM2fOlBurh4cH3t7epKSkABAdHW398C/Wp0+fasV8OVVVr9iXsvj+/fr1s9nXr18/jh8/jtlstu67/D0EBwcDRd8DJfcVfw0AXFxc6Nmzp3W7bdu2+Pr6Eh0dXSqOnJwcTp48yeTJk22+dgsXLrRppuvTpw+zZs3i2Wef5dFHH+Xaa6+94nusqWrV3CxatIjg4GDuuecem/0ffPABycnJPPHEE3YJThRJjLWdmfhKTVLm9HSyf/kFAB8HD8UUor4zuBjYNXaX0+5dFQMHDuTtt99Gp9MRFhaGi4vtr/jLk5iayM7Opnv37nzyySelXgsMDCz3PFdXV5ttRVGwWCwALFiwgFmzZtklvopMmDCBCxcu8Nprr9GsWTP0ej19+vQp1ZxWUayO0qZNGzIyMoiPj79i7U1lXP4eipOmsvZV930V14i99957NsmexWIhLy/PZnvbtm1otVpOnDhRrXtVVbVqbt555x3atm1ban/79u1Zvnx5jYMStpLPlExuKq7Oy1y/HtVoRB8ZidvFToNCiOpRFAV3V3enPCrzV/zlPDw8aN26NeHh4aUSm7K0adOGAwcOkJNzaaqJbdu2odFoiIyMBECn09nUBgB069aN48ePExQUROvWrW0ePj6VW8y3pJLXqo7IyEj27Nljs6/k9rZt25gxYwYjR460dsgtrpGprOJmmsvt3LmzWjFf7o477kCn0/Hiiy+W+XrxHDpRUVFs27bN5rVt27bRpk0btFptGWdWnslksulkHBMTQ3p6urUD+uWCg4MJCwvj1KlTpb4PmjVrZj1uyZIlHD16lF9//ZWffvqJlStX1ijGyqhWcpOQkFBmVhkYGEh8fHyNgxKX5GUXkpmSb7MvqFnFyU36xTkhpNZGCFGRO++8Ezc3NyZMmMDhw4fZsmUL06dPZ9y4cdYmi+bNm3Pw4EFiYmJISUnBaDRy9913ExAQwC233MLvv/9ObGwsW7duZcaMGZw9e9buccbGxrJ//36bx+UJWbHp06fz/vvvs2rVKo4fP85zzz3HwYMHbZLEiIgIPvroI6Kjo9m1axd33303BkPVasjuv/9+jh8/zmOPPUZMTAyffvppmYNpjhw5wv79+0lNTSUjI8Mae3maNm3KK6+8wmuvvcbkyZP59ddf+eeff9i2bRv33Xcfzz77LACPPvoomzdv5tlnn+XYsWOsWrWKZcuW2aXmy9XVlenTp7Nr1y727t3LxIkTueaaa8rsbwNFHa8XLVrE66+/zrFjxzh06BArV67kzTffBGDfvn3MmTOHFStW0K9fP15++WUeeughTp06VeNYK1Kt5KZp06alskYoyhzDwsJqHJS4JPkf2x78JlT8Qsr/QSw4FUv+gYOg1eIz6qZyjxNCCHd3d9avX09qaio9e/bkjjvu4IYbbrAZyTJ16lQiIyPp0aMHgYGBbNu2DXd3d3777TfCw8O5/fbbiYqKYvLkyeTn5zuko+jMmTPp2rWrzWPfvn2ljrv77ruZPXs2s2bNolu3bsTGxjJx4kTcLpvA9P333yctLY1u3boxbtw4ZsyYUeW5csLDw1m7di3ffPMNnTt3Zvny5Tz//POljhs5ciRdu3bl+++/Z+vWrdbYK/Lggw/y888/c+7cOW677Tbatm3LlClT8Pb2tiYv3bp144svvuDzzz+nQ4cOzJkzhwULFth0Jq4ud3d3nnjiCcaOHUu/fv3w9PRkzZo15R4/ZcoUVqxYwcqVK+nYsSP9+/dn9erVNGvWjPz8fP79738zceJERo0aBcC9997LwIEDGTduXKkaQXtS1GqMNXzxxRd58cUXWbJkibXn+ebNm3n88cd59NFHmT17tt0DtZfMzEx8fHzIyMiw+w+h0Whk3bp1jBw5slR7bXX9ue40u767lOGe05q5b0FfmjUqu+086eVXuPDuu3j270/Td+puE6Ejyqq+krKqPHuUVX5+PrGxsbRo0cLmQ7G+sVgsZGZm4u3tjUZTf8eWDBkyhJCQED766KMaXachlNeHH37Iww8/XOMlJGpSVhX9/FXl87taHYofe+wxLly4wIMPPmjthOXm5sYTTzxRpxObq1HSP7b9bRK0Kvvj0stMblSzmYyLE0353HZrbYQnhBB1Rm5uLsuXL2fYsGFotVo+++wzNm3aZNe5dMTVoVrJjaIoLF68mGeeeYbo6GgMBgMRERHo9Xp7x9fgJZVolkpwsbDvTDq3dGlc6tjcPX9iSkhA4+2N58CBtRWiEELUCYqisG7dOhYuXEh+fj6RkZGsXbu2SssfiPqhRpP4eXp62oyHF/aVk1FATnqBzT6XAD2NPMqetyZz3ToAvIcNRSOJphCigTEYDGzatMnZYVy1Jk6caJd+O3VBtZKbnJwcXnjhBTZv3kxSUlKpMfKO7gXdUJSstXHVa/n2yetRNKWHh6pGI1k//wyA94gRtRKfEEIIURdVK7mZMmUKv/76K+PGjSM0NLTKczGIyinZ3yYw3KvMxAYgZ+dOzOnpaBs1wr2cIXtCCCFEQ1Ct5Gb9+vX8+OOPpaZ/FvaVdNq25ibo4npSJrOF9DwjAZ6Xmp4y160HipqklEpM3iWEEELUV9Uaz+bn54e/v7+9YxGXUVW11MzEQc28+PnvBDrP/5lH1uy37rcUFpJ1sZ3Ze+TI2gxTCCGEqHOqldw8++yzzJkzh9zcXHvHIy7KSs0nL8tosy+omRdN/NzJKTSz70w6ZkvRFEU5f/yBJSsLl+BgDN26OSNcIYQQos6oVvvF0qVLOXnyJMHBwTRv3rzUZFl//fWXXYJryErOTKx3d8E7wICnCl56F7IKTBxNyKR9mM+lJqnhw1Hq6eRSQgghRGVVK7m5VdYscrjkONvkJjDcC0VR0CrQtZkfvx1L5s/TaUT56ci6uAK4943SJCWEqBsmTpxIeno631xc684R7DWjrj1s3bqVgQMHkpaWhq+vr7PDcZja+LraQ7WSm7lz59o7DlFCytlsm+3AcC/r8x7Fyc0/adyWcxw1NxfXxo1x69ixtsMUQtQREydOZNWqVUDR4ofh4eGMHz+ep556qlIrhFd03ep8mL322mtUY3WfUhRF4euvvy7zj+oxY8Ywso72M9y6dSuvvPIKu3fvJjMzk4iICB577DHuvvvuK567du1a3njjDfbt24fZbKZly5bccccdTJs2Tfq7VlKN2jD27t3Lxx9/zMcff1zmImai+lLO2NbcBDT1tD7v0dwPgD2xqWRt2gyA1+DBMiRfiAZu+PDhxMfHc/z4cR599FHmzZvHkiVLyjy2eOkcR/Hx8XF4DYbBYKjyope1Zfv27XTq1Im1a9dy8OBBJk2axPjx4/nhhx8qPO+///0vY8aMoWfPnqxfv57Dhw+zdOlSDhw4UOP1sRqSaiU3SUlJDBo0iJ49ezJjxgxmzJhB9+7dueGGG0hOTrZ3jA1ObmYhORm2v3gCmlyquenS1BetRiE5PYfMX7YA4DVEphcXoqHT6/WEhITQrFkzHnjgAQYPHsx3F9ebmzhxIrfeeisLFy4kLCyMqKgoAA4dOsSgQYMwGAw0atSIe++9l+zsoprjefPmsWrVKr799lsURUFRFLZu3QpAXFwco0ePxtfXF39/f2655RZOnz5tjaX4fsUGDBjAjBkzePzxx/H39yckJIR58+bV6P1++OGHpRKo5557jqCgILy8vJgyZQpPPvkkXbp0sb6+Z88ehgwZQkBAAD4+PvTv379UP1FFUVixYgW33XYb7u7uREREWMux2Lp162jTpg0Gg4GBAwfavHeAp556imeffZa+ffvSqlUrHnroIYYPH87//ve/ct/P7t27ef7551m6dClLliyhb9++NG/enCFDhrB27VomTJhgPfbtt9+mVatW6HQ6IiMjSyU+iqLwzjvvcNNNN+Hu7k5UVBQ7duzgxIkTDBgwAA8PD/r27cvJkyet58ybN48uXbrwzjvv0LRpU9zd3Rk9ejQZGRnlxmyxWFi0aBEtWrTAYDDQuXNnvvrqK6Bo1O/gwYMZNmyYtRYvNTWVJk2aMGfOnHKvaQ/VSm6mT59OVlYWf//9N6mpqaSmpnL48GEyMzOZMWOGvWNscC6UaJJycdXgG+xu3XbXufDv3uHMa1YIWZlo/f0xdO1a22EK0SCoqoolN9cpj5o26xgMBpsams2bNxMTE8PGjRv57rvvyMnJYcSIEfj5+bFnzx6+/PJLNm3axLRp0wCYNWsWo0ePttYIxcfH07dvX4xGI8OGDcPLy4vff/+dbdu24enpyfDhwyusEVq1ahUeHh7s2rWLF198kQULFth1UctPPvmEhQsXsnjxYvbu3Ut4eDhvv/22zTFZWVlMmDCBP/74g507dxIREcHIkSPJyrKtLZ8/fz6jR4/m4MGDjBw5knHjxpGWlgYUJXa33347o0aNYv/+/dYk6koyMjIqbFb65JNP8PT05MEHHyzz9eJE7uuvv+ahhx7i0Ucf5fDhw9x3331MmjSJLVu22Bz/7LPPMn78ePbv30/btm0ZO3Ys9913H7Nnz+bPP/9EVVXr17rYiRMn+OKLL/j+++/56aef2LdvX7nxACxatIjVq1ezfPly/v77bx555BHGjx/Ptm3bUBSFVatWsWfPHl5//XUA7r//fho3buzw5KZaDbE//fQTmzZtsmb+AO3atePNN99k6NChdguuoUo+a/tD5t/YE02JmYnn39KBhAVfkwZ4DhqIotXWYoRCNBxqXh4x3bo75d6Rf+1FcXe/8oElqKrK5s2b2bBhA9OnT7fu9/DwYMWKFeh0OiwWC2+88Qb5+fmsXr0aDw8PAJYtW8aoUaNYvHgxwcHBGAwGCgoKCAkJsV7n448/xmKxsGLFCmtz+MqVK/H19WXr1q3lfg506tTJ2mczIiKCZcuWsXnzZoYMGVLl91iWN954g8mTJzNp0iQA5syZw88//2ytiQIYNGiQzTnvvvsuvr6+/Prrr9x0003W/RMnTuSuu+4C4Pnnn+f1119n7969NGvWzFprsnTpUgAiIyM5dOgQixcvLje2L774gj179vDOO++Ue8zx48dp2bJlqRHIJb300ktMnDjRmnTMnDmTnTt38tJLLzHwskWTJ02axOjRowF44okn6NOnD8888wzDhg0D4KGHHrKWVbHi74fGjYsWZ37jjTe48cYbWbp0qc33AEBBQQHPP/88mzZtok+fPgC0bNmS33//nZUrVzJixAgaN27MO++8w/jx40lISGDdunXs27evRv3AKqNaNTcWi6XMwnd1dS21zpSoupQ425qby/vbFFMtFrI2X+pvI4QQP/zwA56enri5uTFixAjGjBlj0/TTsWNHdLpLC+8eO3aMzp07WxMbgH79+mGxWIiJiSn3PgcOHODEiRN4eXnh6emJp6cn/v7+5Ofn2zRzlNSpUyeb7dDQUJKSkoCiv+iLr+XpWfp3XmXExMTQq8TyMyW3ExMTmTp1KhEREfj4+ODt7U12djZnzpwpN1YPDw+8vb1JSUkBIDo6mt69e9scX/zhXpYtW7YwadIk3nvvPdq3b1/ucZWtqYuOji61QkC/fv2Ijo4u9z0EBwcDRd8Dl+/Lz88nM/PShLHh4eHWxAaK3ld53w8nTpwgNzeXIUOG2HztPvroI5tmujvvvJPbbruNF154gZdeeomIiIhKvc+aqFbqNGjQIB566CE+++wzwsLCADh37hyPPPIIN9xwg10DbIhKjZRqUvoHPf/wYUyJiVjcDBR2cs5flUI0BIrBQORfe51276oYOHAgb7/9NjqdjrCwsFJ/HV+exNREdnY23bt355NPPin1WmBgYLnnlfyjWFEU6x/ECxYsYNasWXaJryITJkzgwoULvPbaazRr1gy9Xk+fPn1KNadVFGtV/Prrr4waNYpXXnmF8ePHV3hsmzZt+OOPPzAajVesvamMy69RXMNW1r7qVkoU14j9+OOPNgmRxWKxKc/c3Fz27t2LVqvl+PHj1bpXVVWr5mbZsmVkZmbSvHlzWrVqRatWrWjRogWZmZm88cYb9o6xQTEVmklPyLHZF9DUq9RxxaOk/vCP4I8SyzQIIexHURQ07u5OeVR1BKSHhwetW7cmPDy8UtX+bdq04cCBA+TkXPqds23bNjQaDZGRkQDodDrMZrPNed26deP48eMEBQXRunVrm4ePj0+VYi5W8lrVERkZyZ49e2z2ldzetm0bM2bMYOTIkbRv3x69Xm+tkamsqKgodu/ebbNv586dpY7bunUrN954I4sXL+bee++94nXHjh1LdnY2b731VpmvF8/nExUVxbZt22xe27ZtG+3atavkOyjfmTNnOH/+vHV7586dNt8Pl2vXrh16vZ4zZ86U+j5o0qSJ9bhHH30UjUbD+vXref311/nl4txsjlStmpumTZvy119/sWnTJo4ePQoUFfZgaR6psQvnc7CpmVSgUePSNTfFa0ltD+tI2KkL3NKlcaljhBCiInfeeSeLFy9mwoQJzJs3j+TkZKZPn864ceOszRjNmzdnw4YNxMTE0KhRI3x8fLj77rtZsmQJt9xyCwsWLKBJkyb8888//O9//+Pxxx+3+WCzh9jYWPbv32+zr6ymjenTpzN16lR69OhB3759WbNmDQcPHqRly5Y253300Uf06NGDzMxMHnvsMQxVrCG7//77Wbp0KY899hhTpkxh7969fPjhhzbHbNmyhZtuuomHHnqI//u//yMhIQEoShbL61Tcu3dvHn/8cR599FHOnTvHbbfdRlhYGCdOnGD58uVce+21PPTQQzz22GOMHj2arl27MnjwYL7//nv+97//seni50JNuLm5MWHCBF566SXrIKHRo0eX6m8D4OXlxaxZs3jkkUewWCxce+21ZGRk8Mcff+Dq6sp9993Hjz/+yAcffMCOHTvo1q0bjz32GBMmTODgwYP4+fnVON7yVHueG0VRGDJkCNOnT2f69OmS2NhJSomZiX2D3HHV23YWLvznHwpPnULVavkzqC07Tl6ozRCFEPWEu7s769evJzU1lZ49e3LHHXdwww03sGzZMusxU6dOJTIykh49ehAYGMi2bdtwd3fnt99+Izw8nNtvv52oqCgmT55Mfn4+3t7edo9z5syZdO3a1eZR1txqd999N7Nnz2bWrFl069aN2NhYJk6ciJubm/WY999/n7S0NLp168a4ceOYMWNGlefKCQ8PZ+3atXzzzTd07tyZ5cuX8/zzz9scs2rVKnJzc1m0aBGhoaHWx+23317htRcvXsynn37Krl27GDZsGO3bt2fmzJl06tTJOhT81ltv5bXXXuOll16iffv2vPPOO6xcuZIBAwZU6X2UpXXr1tx+++2MHDmSoUOH0qlTp3JrkqBoRNYzzzzDokWLiIqKYvjw4fz444+Eh4eTnJzM5MmTmTdvHt0urns4f/58goODuf/++2sca0UUtQpjDX/55RemTZvGzp07S30DZ2Rk0LdvX5YvX851111n90DtJTMzEx8fHzIyMuz+Q2g0Glm3bh0jR46sdnvpr5/GcPi3c9bt1j2CGDalg80xqas/IvH559H16MmQpmOwqLBj9iBCfar214cz2aOsGgopq8qzR1nl5+cTGxtLixYtbD4U6xuLxUJmZibe3t5o6vGadEOGDCEkJKTGE+A1hPKaN28e33zzTalasqqqSVlV9PNXlc/vKt311VdfZerUqWVe1MfHh/vuu4+XX365KpcUJaSUGAYeUEZn4uzffgPAd+AAOjYuat+W2hshREOXm5vLyy+/zN9//83Ro0eZO3cumzZtspn8TjQMVUpuDhw4wPDhw8t9fejQoezd65xRBfWBxaKScq7izsSW3FxyL3Zk8+x/Pde0agRIciOEEIqisG7dOq6//nq6d+/O999/z9q1a6XbRANUpQ7FiYmJFVb1uri4yPILNZCZnIepwHZUQsmam5xdu1ALC3ENC0PXqhV9zMm88+spdpyS5EYI0bAZDAa7dKptqObNm1fjJTHqiirV3DRu3JjDhw+X+/rBgwcJDQ2tchBvvvkmzZs3x83Njd69e5caYleezz//HEVRylwt9mp04Zzt/DYGL1c8fPQ2+7J//RUAzwH9URSFns39eenOzqy5r/wJpIQQQoiGpErJzciRI3nmmWfIz88v9VpeXh5z5861mb66MtasWcPMmTOZO3cuf/31F507d2bYsGHWWSvLc/r0aWbNmlWnOy9XVcnkpuQQcFVVrf1tPK6/vuhfvQt3dG9CY9+rpzOxEEII4UhVSm6efvppUlNTadOmDS+++CLffvst3377LYsXLyYyMpLU1FT++9//VimAl19+malTpzJp0iTatWvH8uXLcXd354MPPij3HLPZzN133838+fNt5i+42qWet+1v0yjMNrkpPHEC0/l4FJ0OjxJTfwshhBCiSJX63AQHB7N9+3YeeOABZs+ebV0HQ1EUhg0bxptvvmmd+KkyCgsL2bt3L7Nnz7bu02g0DB48mB07dpR73oIFCwgKCmLy5Mn8/vvvFd6joKCAgoIC63bxGhpGoxGj0VjpWCuj+HrVvW5KiZobnxA3m2tlXFzx1dCzJ2YXF8wXX8srNPP5n2fZdyadV0d3KrXIZl1U07JqSKSsKs8eZWU0GotWArdY6vVaecW/v4vfq6iYlFfl1aSsLBYLqqpiNBrRllgQuio/11WeobhZs2asW7eOtLQ0Tpw4gaqqREREVGumwZSUFMxmc6mEKDg42DrzcUl//PEH77//fqXH4S9atIj58+eX2v/zzz/jXo3Vditj48aNVT5HNUNGkidwKTE5GrufU2mXvjGafPMN7sDpgEbsX7fOut9sgaV/aikwK7T/aj1lrLNZZ1WnrBoqKavKq0lZubi4EBISQnZ2dqn1huqjrKysKx8krKS8Kq86ZVVYWEheXh6//fYbJpPJ5rXc3NxKX6faa477+fnRs2fP6p5eLVlZWYwbN4733nuPgICASp0ze/ZsZs6cad3OzMykadOmDB061CGT+G3cuJEhQ4ZUeQKxlLhs/vez7YybN/7fEOvsxJacHE7992kAet53H65Nm9ocuz5zPxujk7AEt2Vk/7rfVFeTsmpopKwqzx5llZ+fT1xcnHV17fpKVVWysrLw8vKq8hpWDZGUV+XVpKzy8/MxGAxcf/31ZU7iV1nVTm7sISAgAK1WS2Jios3+xMTEMtexOHnyJKdPn2bUqFHWfcVVXi4uLsTExNCqVSubc/R6PXq97YgjKFoZ1VEfFNW5dmaSbSdt7wA33D0vfWGz9u0DkwnXpk1xL6Of0fWRQWyMTmLbyVRmDC69wFld5civQ30jZVV5NSkrs9lctFimRlNvZ6KFS787i9+rvU2cOJH09HS++eYbu1+72IcffsjDDz9sXVDSka5UXlu3bmXgwIGkpaXh6+vr8HgcwV7lWZPvLY1Gg6IoZf4MV+Vn2qk/uTqdju7du7N582brPovFwubNm+nTp/TQ5rZt23Lo0CH2799vfdx8880MHDiQ/fv307REbcbV5EKJyfv8S3QmzrnYB8mjb98yz78+oqgma+8/aWQXmMo8RghRf02cOBFFUVAUBZ1OR+vWrVmwYEGpqv3qXLc602289tprpRaTrA5FUcpNkMaMGcOxY8dqfI/atG/fPu68806Cg4Nxc3MjIiKCqVOnXnXvo65z+p8lM2fO5L333mPVqlVER0fzwAMPkJOTw6RJkwAYP368tcOxm5sbHTp0sHn4+vri5eVFhw4d0Ol0znwrNXKh1EgpD5vtnO3bAfAoI+kDaNbIg2aN3DFZVHbKbMVCNEjDhw8nPj6e48eP8+ijjzJv3jyWLFlS5rGO7k/k4+Pj8BoMg8FQ5UUvnemHH37gmmuuoaCggE8++YTo6Gg+/vhjfHx8eOaZZ5wdXr3i9ORmzJgxvPTSS8yZM4cuXbqwf/9+fvrpJ2sn4zNnzhAfH+/kKB0v9Xz5c9wYE5MoPHESFAWPa8ofAn7dxdqb34/LLNFC2INqUcnLKnTqQ7VUem1j9Ho9ISEhNGvWjAceeIDBgwfz3XffAZdqYBYuXEhYWBhRUVEAHDp0iEGDBmEwGGjUqBH33nsv2dlFv4/mzZvHqlWr+Pbbb621Qlu3bgUgLi6O0aNH4+vri7+/P7fccgunT5+2xlKyxmfAgAHMmDGDxx9/HH9/f0JCQmo8G+6HH35YKoF67rnnCAoKwsvLiylTpvDkk0/SpUsX6+t79uxhyJAhBAQE4OPjQ//+/fnrr79srqEoCitWrOC2227D3d2diIgIazkWW7duHW3atMFgMDBw4ECb916W3NxcJk2axMiRI/nuu+8YPHgwLVq0oHfv3rz00ku888471mN//fVXevXqhV6vJzQ0lCeffNKmBm7AgAFMnz6dhx9+GD8/P4KDg3nvvfesFQNeXl60bt2a9evXW8/ZunUriqLw448/0qlTJ9zc3LjmmmsqnJgX4Ntvv6Vbt264ubnRsmVL5s+fb41lwYIFhIWFceHCpT+ob7zxRm644Qanjyhzap+bYtOmTWPatGllvlb8g1Qee1R7OltBrpHstAKbff6X1dzk7CiqtXFr3x5tBX8JXR8RyBd7zpJnNJd7jBCi8vJzjHzw2B9OjeGeJddi8KperbTBYLD54Nm8eTPe3t5s3LgRi8VCTk4OI0aMoE+fPuzZs4ekpCSmTJnCtGnT+PDDD5k1axbR0dFkZmaycuVKAPz9/TEajQwbNow+ffrw+++/4+LiwnPPPcfw4cM5ePBgubXoq1atYubMmezatYsdO3YwceJE+vXrx5AhQ6r1/kr65JNPWLhwIW+99Rb9+vXj888/Z+nSpbRo0cJ6TFZWFhMmTOCNN95AVVWWLl3KyJEjOX78OF5el9bymz9/Pi+++CJLlizhjTfeYNy4cRw8eBBvb2/i4uK4/fbb+c9//sO9997Ln3/+yaOPPlphbBs2bCAlJYXHH3+8zNeLk7Rz584xcuRIJk6cyOrVqzl69ChTp07Fzc3NJhlctWoVjz/+OLt372bNmjU88MADfP3119x222089dRTvPLKK4wbN44zZ87YjAx+7LHHeO211wgJCeGpp55i1KhRHDt2rMz+LL///jvjx4/n9ddf57rrruPkyZPce++9AMydO5f//ve//PTTT0yZMoWvv/6aN998k+3bt7Nv3z6n91dzes2NKD15n0ar4Bt86Zsxt7i/TTlNUsX6RwZyYO5QXryjs/2DFEJcNVRVZdOmTWzYsIFBgwZZ93t4eLBixQrat29P+/bt+eqrr8jPz2f16tV06NCBQYMGsWzZMj766CMSExPx9PTEYDBYa4RCQkLQ6XSsWbMGi8XCihUr6NixI1FRUaxcuZIzZ85U+Adpp06dmDt3LhEREYwfP54ePXrY9LmsqTfeeIPJkyczadIk2rRpw5w5c+jYsaPNMYMGDeLf//43bdu2JSoqinfffZfc3Fx+vbi0TbGJEydy11130bp1a55//nmys7OtC0O//fbbtGrViqVLlxIZGcndd9/NxIkTK4zt+PHjQFHf0Yq89dZbNG3alGXLltG2bVtuvfVW5s+fz9KlS21qQzp37szTTz9NREQEs2fPxs3NjYCAAKZOnUpERARz5szhwoULHDx40Ob6c+fOZciQIXTs2JFVq1aRmJjI119/XWYs8+fP58knn2TChAm0bNmSIUOG8Oyzz1prmbRaLR9//DGbN2/mySef5LHHHuPNN98kPDy8wvdYGyS5qQNK9rfxDXZH61L0pVFVlZztF5ObfmV3Ji6md9Fi0GkrPEYIUX/98MMP1iHsI0aMYMyYMTZ/7Xfs2NGmVuXYsWN07twZD49LNcX9+vXDYrEQExNT7n0OHDjAiRMn8PLywtPTE09PT/z9/cnPz+fkyZPlntepUyeb7dDQUOtSO/fff7/1Wp6e1ZusKyYmhl69etnsK7mdmJhoTQB8fHzw9vYmOzubM2fOlBurh4cH3t7epKSkABAdHU3vErPElzUI5nLFE9tdSXR0NH369LEZQt2vXz+ys7M5e/ZsmfFptVoaNWpkk8gVd+0ouZTR5XH6+/sTGRlJdHR0mbEcOHCABQsW2Hxdpk6dSnx8vHXOmZYtW/LSSy+xePFibr75ZsaOHVup9+lodaJZqqFLLbmm1GVNUoUnTmBKTkbR6zF07Vrpa2bkGvFxl2HDQjQkAwcO5O2330an0xEWFoaLi+2v+MuTmJrIzs6me/fufPLJJ6VeCwwMLPe8kk0fiqJYayMWLFjArFmz7BJfRSZMmMCFCxd47bXXaNasGXq9nj59+pTqYF1RrNXRpk0bAI4ePXrFRKgyyorv8n3FyVFNYs7Ozmb+/PncfvvtpV67fA6a3377Da1Wy+nTpzGZTE5vkgJJbuqEkjU3/pd1Ji4eAu7eoweaMubrKSk1p5Bx7+/iZHI2+54ZKjU5QtSAm4cr9yy51ukxVJaHhwetW7eu9PFt2rThs88+Iycnx5r4bNu2DY1GQ2Rk0XxZOp0Os9m2H1+3bt1Ys2YNQUFBdpsMNSgoqMYjnyIjI9mzZw/jx4+37tuzZ4/NMdu2beOtt95i5MiRQFHH6OIamcqKiooq1cF4586dFZ4zdOhQAgICePHFF8tsBkpPT8fX15eoqCjWrl2LqqrWBGXbtm14eXnRpEmTKsVZlp07d1qbjdLS0jh27Ji1c3lJ3bp1IyYmpsLvqTVr1vC///2PrVu3Mnr0aJ599lnmzp1b4zhryvnpVQOnqioXSo6Uurwz8baLQ8D7Vi7T93N3JT3XSL7RwvaTVfuBFULYUjQKBi+dUx+KA9eKu/POO3Fzc2PChAkcPnyYLVu2MH36dMaNG2dt1mjevDkHDx4kJiaGlJQUjEYjd999NwEBAdxyyy38/vvvxMbGsnXrVmbMmGHTdGIvsbGxNvOb7d+/n5ycnFLHTZ8+nffff59Vq1Zx/PhxnnvuOQ4ePGjTxBMREcFHH31EdHQ0u3bt4u6778ZgMFQpnvvvv5/jx4/z2GOPERMTw6effnrFwS3F/Z1+/PFHbr75ZjZt2sTp06f5888/efzxx7n//vsBePDBB4mLi2P69OkcPXqUb7/9lrlz5zJz5ky71IgsWLCAzZs3c/jwYSZOnEhAQEC58xjNmTOH1atXM3/+fP7++2+io6P5/PPPefrpotnyz549ywMPPMDixYu59tprWblyJc8///wVE73aIMmNk+VlGSnIsZ1kq3gCP9VkIvfPPwFwv+aaSl1PURQGtS3662fz0aQrHC2EaMjc3d1Zv349qamp9OzZkzvuuIMbbriBZcuWWY+ZOnUqkZGR9OjRg8DAQLZt24a7uzu//fYb4eHh3H777URFRTF58mTy8/PtvqwNFM2H1rVrV5vHvn37Sh139913M3v2bGbNmkW3bt2IjY1l4sSJNk0o77//PmlpaXTr1o1x48YxY8aMKtcYhYeHs3btWr755hs6d+7M8uXLef7556943i233ML27dtxdXVl7NixtG3blrvuuouMjAyee+45ABo3bsy6devYvXs3nTt35v7772fy5MnWhKKmXnjhBR566CG6d+9OQkIC33//fbmj24YNG8YPP/zAzz//TM+ePbnmmmt45ZVXaNasGaqqMnHiRHr16mUd7Txs2DAeeOABxo8fb51OwFkUtbK9nOqJzMxMfHx8yMjIcMjaUuvWrWPkyJGVnib6/PE0vl566YdU66rh3tf6o9Eo5B06zOk770Tj5UWbnTtQtJVrYtoak8TElXsI8XZjx+xBdXIdlOqUVUMlZVV59iir/Px8YmNjadGiRb1eW8pisZCZmYm3t3ed6CPhKEOGDCEkJISPPvqoRte52surNpeHqElZVfTzV5XPb+lz42RpCbarnPoGGdBcrIbOvdhW7N69e6UTG4BrWjbCXaclITOfv89n0qGxj/0CFkKIOio3N5fly5czbNgwtFotn332GZs2barRKvHi6nT1pZ/1TFpiieQm+FJ/G2tyU8XV191ctVzbumi24s3R0jQlhGgYFEVh3bp1XH/99XTv3p3vv/+etWvXMnjwYGeHJmqZ1Nw4WXqJmhu/kKLJ+1SzmdyLE0a596pacgNwQ1QQPx9J5JejiTw0OKLmgQohRB1nMBjYtGmTs8OokwYMGFDpuXbqA0lunCwtwbbHf3FyU3DsGJbMTDQeHriVM0yvIgPbBnFz5zAGtwu2S5xCCCHE1UKSGycyGc1kXci32Ve87EJxk5ShWzcUl6p/mYK83Hj9rspP+ieEEELUF9LnxokykvIoWUtYMrmpan8bIYR9NKQqfCHqCnv93EnNjROVHCnl6adH5+aCarGQu+fi/DY9e9ToHscTs1h/OIHxfZrh6169lYWFaEhcXV1RFIXk5GQCAwPr5FQK9mCxWCgsLCQ/P/+qHNpc26S8Kq+6ZaWqKsnJyaWWkqgOSW6cKD2x9IKZAAUnTmBOT0cxGDB06FCje0z/bB9HE7II9XHjzh5Na3QtIRoCrVZLkyZNOHv2LKdPn3Z2OA6jqip5eXkYDIZ6m8DZk5RX5dWkrBRFoUmTJmirMP1JWSS5caKSw8D9SjZJde2CUsPsdUSHUI4mZPHT4QRJboSoJE9PTyIiIjAajc4OxWGMRiO//fYb119/vUwOWQlSXpVXk7JydXWtcWIDktw4Vclh4L4hRXPc5BUPAbdDf5sRHUN4ZdMxfj+eQnaBCU+9fMmFqAytVmuXX7J1lVarxWQy4ebmJh/WlSDlVXl1oayk4dBJVFUt1eemeBh47r79ABi6da/xfSKCPGkZ4EGh2cIvstaUEEKIBkCSGyfJzSjEWGC22ecb7I4xPh5TfDxotRg61qy/DRS1Xw7vEALAT4fja3w9IYQQoq6T5MZJSk7e56LX4umrJ+/iSrdubduicXe3y71GdAgFYMvRZPIKzVc4WgghhLi6SXLjJKWapILdUTTKpSaprvabgK9DY2+a+htw0SocS8yy23WFEEKIukh6lzpJ6QUzi2ppimtuDF272O1eiqKwcmJPmvi54+ZafztICiGEECDJjdOklxwGHuKOJTeX/OhoANztWHMD0DrIy67XE0IIIeoqaZZykpJ9bnyD3ck7fBjMZlyCg3EJDXXIfVVVJSOv/s7dIYQQQkhy4wTGAjPZqQU2+/xC3Mm7rL+NI2bA3B2bysCXtvLgJ3vtfm0hhBCirpDkxgnSk2ybpFDAJ8jd2t/G3Y79bS4X6uPG6Qu5bD95gaTM/CufIIQQQlyFJLlxgpIzE3v5u+HiqrmsM7F9+9sUa+rvTvdmfqgqfH9Q5rwRQghRP0ly4wQl+9v4hbhTGHsac0YGil6PW9u2Drv3zZ3DAPhu/zmH3UMIIYRwJklunKCsYeDWyfs6dkDR6Rx27xs7haLVKBw4m8GJpGyH3UcIIYRwFklunKD0MHAP8g4eBMDQubND7x3gqWdAm0AAvtp71qH3EkIIIZxBkptaplrUUn1u/ILdyT90CABDx04Oj+HOHk0A+N9fZzGZLQ6/nxBCCFGbZBK/WpaVlo/JaJtQePu5cPbYMQC7LJZ5JYPaBjO2dzijOoWhccCQcyGEEMKZJLmpZSWbpHRuWrTnToDJhLZRI1zCwhweg85Fw/O3dXT4fYQQQghnkGapWlZywUzfEA/yD/8NgKFDB4dM3ieEEEI0JJLc1LJS/W1C3Mk7VNSZ2K1T7damnEjKYt53f7Nmz5lava8QQgjhSJLc1LKM5BI1N0EG8g8dBsDQsXaTmx0nL/Dh9tOs3HYaVVVr9d5CCCGEo0hyU8sykvNstr08FQpjYwFwq+Xk5ubOjdG5aDiakMWBsxm1em8hhBDCUSS5qUVmk4WsC7ZrOrllFM0U7NqkCS5+frUaj4+7K6M6FXVg/mjHP7V6byGEEMJRJLmpRVkX8inZ+uN6JhoompnYGf59TTgA3x88T1pOoVNiEEIIIexJkptaVLJJys3DFcvRA0DtTN5Xli5NfenQ2JtCk4Uv98Y5JQYhhBDCniS5qUUlkxvvQAN5B4tnJnZOzY2iKIy7phkAH+88g8UiHYuFEEJc3SS5qUUlR0p5eymYEhNBo8GtXTsnRVXUsbhFgAcjO4ZSYJLlGIQQQlzdZIbiWlSy5sbdXDRCSd+qJRoPD2eEBIBBp+WXR/vLBIJCCCHqBam5qUUZSSX63GQWjZRyZq1NMUlshBBC1BeS3NQSi0Ul84JtcqOLPw6APirKGSGVoqoqvx5L5pNdMixcCCHE1UuapWpJdlo+FpNtZ12XY/uAulFzA7A7NpUJH+zGXaflpo5h+Li7OjskIYQQosqk5qaWlOxv46rXoMSdAMCtjtTc9GrhT9sQL3ILzXyyW2pvhBBCXJ0kuaklmSWXXfBQUQDXpk3Renk5J6gSFEVhynUtAVi1/TSFMnJKCCHEVUiSm1pSsjOxh5oN1J1am2I3dw4jyEtPYmYB3x847+xwhBBCiCqT5KaWlJqdODuh6N92dSu50blomNC3OQDv/X5KVgsXQghx1ZHkppaUnMBPn3gSqDudiS93d+9w3HVajiZksfVYsrPDEUIIIapEkptaoKpq6Q7FcRcXzKxjzVIAvu467u4dTkSQJy4amf9GCCHE1UWGgteC3MxCTIW2nXMNuUloAwNwCQx0UlQVmzkkktkjotBIciOEEOIqIzU3taBkZ2KtRkVfkFEna22KGXRaSWyEEEJclaTmphZkppRYU0rJRUHFLaru9bcpKa/QzGe7z9Al3Jdu4X7ODkeUoKoqhZZCCs2FmC1mTKoJs8WMWTVjtpgxqkab7ctfN1lMmCymcl+zqBYsWFBVtei5akGl6Lmqqtbnl+8vfl7lcy6+pqJa31ep94pq875L7i++59ncs+zasQulRHJe1jnlXffyfZTXp14p/ufSfYqXMSneZ/23jOVNSr5W0XVK7q/pPRRFwWK2cDr3NH/v/RutRlvhvSuKtWQ5lBVPee+jMmWHUva1K7rP5de60nGVvY7FYuFwwWFyj+ei1WqveJ/y3tsVXy/rOmWUcZnlddlxZZZFie+RylynVDlV4jomk4kEcwLOJMlNLSiZ3LjlFnXSrcs1N8WWbIjhg22xXN8mkNX39HJ2OHWeqqrkm/PJNeaSZ8ojz5RHrunic2OedV9ZjwJzAYXmQgothRjNxqJtSyGFpkJSM1NZ/t1y62vFCY3RYnT2W66T9sXuc3YIV40dMTucHcJV5fs93zs7hKtCU21T7uEep92/TiQ3b775JkuWLCEhIYHOnTvzxhtv0KtX2R+k7733HqtXr+bw4cMAdO/eneeff77c4+uCzAv5Ntv6C2cAcGtf92tuJvZtzqodp/ntWDJ7/0mje7OGUXuTa8wlrSCNtPyLj4I0MgsyyTJmkVWYRXZhNlmFRc9L7jOpJscElV25w1wUF7QaLVpFi1ajxVXjan2uVbS4aFxsjnHRuFz6V6O1vqZBg0YpeiiKUvQcDShYn1v3KxrrX29l7bf5V7HdLn6OQtH1LyrvL//yFnkt/us65mgMkW0j0Wq1ZdY+XOkaV7o/UGYNk1qiiqesWqCS55U8p6zXKrrOpX/KOKac6xQzW8ycOHGCVq1aodFoyr1OqXuUVWtWiRq3iuKpqOwqvO/lx5VVTiXvWdZxatnvo2RMZouZhIQEgoODrd8bl8d3eTmVGV9Zx5URX1lf08qU3eUxl/neqlOmZR1XQZkWs6gWvPO9cSanJzdr1qxh5syZLF++nN69e/Pqq68ybNgwYmJiCAoKKnX81q1bueuuu+jbty9ubm4sXryYoUOH8vfff9O4cWMnvIMrK6vmRuPpiWuTJk6KqPLCG7lzR7cmrPkzjsU/HWXNvddctSuIF5oLSc5LJik3icTcRJJykkjKTeJC/gXS8tNIzU8lrSCN9Px08s35V77gFbhp3TC4GHB3dcfgYrjiQ6/V46p1Ra/Vo9Pq0Gl0uGpd0apa9u3Zx3V9r8OgN6DT6Kyv67RFD1eNK64aV2vy0FAZjUbWnV7HyHYjcXWVtdEqYjQaWXduHSO7SFlVhtFoZN26dYy8XsrrSorLypmcnty8/PLLTJ06lUmTJgGwfPlyfvzxRz744AOefPLJUsd/8sknNtsrVqxg7dq1bN68mfHjx9dKzFWVVaLmxpB/AX2bNlfNh9BDgyP4ev85dsem8uuxZAZElk4664KswizOZZ/jbNZZzmWfIy4rjvPZ50nKLUpi0grSqnQ9nUaHn5sf/m7++Op98dH74KXzwlPnibfOG09XT7x0XtbH5dsGFwMaxT799Y1GIxmuGXQO7Cy/VIUQohKcmtwUFhayd+9eZs+ebd2n0WgYPHgwO3ZUrh04NzcXo9GIv7+/o8KsEbPRQnZ6gc0+t/wL6Nv0c1JEVRfma2BCn2a893ssSzbEcH1EoNNGUhWYCzidcZpTGac4lXGK2IxY4rLiOJd9joyCjCuer9PoCHQPJNg9mCD3IILcgwgwBFiTGD+9H75uvvi7+ePu4n7VJKBCCCEucWpyk5KSgtlsJjg42GZ/cHAwR48erdQ1nnjiCcLCwhg8eHCZrxcUFFBQcCm5yMzMBIr+GjYa7dsZs/h6l183Iymv1GgLQ14Krq1a2f3+jjSlXzM+3X2Gv89n8t3+s9zYMaRG1yurrC5nUS3EZcVxNPUoMekxnEw/SWxmLOdzzmNRy1/Q00/vR2PPxtZHmEcYwe7BBBoCCXIPwkfnU+mExWRyUN+ZKrpSWYlLpKwqT8qqaqS8Ks9RZVWV6zm9WaomXnjhBT7//HO2bt2Km5tbmccsWrSI+fPnl9r/888/4+7u7pC4Nm7caH2en6wFLt3HxZSLizmfvRdSyXdym2RV9Q9SiMtWSIz5i3Vx9rnmxo0bUVWVFEsKceY44k3xnDefJ94cTyGFZZ5jUAwEagIJ1AYSqAmkkbYRfho//DR+6BU9mIGMiw8g4+J/Jzhhn6Cd5PLvK1ExKavKk7KqGimvyrN3WeXm5l75oIucmtwEBASg1WpJTEy02Z+YmEhISMU1Ay+99BIvvPACmzZtolOnTuUeN3v2bGbOnGndzszMpGnTpgwdOhRvb/v25jYajWzcuJEhQ4ZY+0Yc+SOeP/689KFqyEsBoP+4f6O18/0dbYSq2qWZpsBcwMGkg6zdsZY8vzwOpR4ivSC91HF6rZ4I3wja+rWltW9rWvi0oIV3Cxq5NWpQzUVlfV+JsklZVZ6UVdVIeVWeo8qquOWlMpya3Oh0Orp3787mzZu59dZbAbBYLGzevJlp06aVe96LL77IwoUL2bBhAz169KjwHnq9Hr1eX2q/q6urw75BL792brpt7YNb/gVcQkNxa9TIIfeuTWolkx2LauFo6lF2nN/BjvM72Je0j0LLxXKJL/pHr9XTvlF72jVqR7tG7Yjyj6K5T3NcNFd15aJdOfJ7tr6Rsqo8KauqkfKqPHuXVVWu5fRPjpkzZzJhwgR69OhBr169ePXVV8nJybGOnho/fjyNGzdm0aJFACxevJg5c+bw6aef0rx5cxISimZB9PT0xNPT02nvozwl57gx5F1A3ybCSdHYR3JWAS9tiMHVReG5WzuWeUxGQQa/nf2N38/+zs74naVGKjVya0SwOZjhHYbTPbQ7Uf5RuGrlF4YQQoiac3pyM2bMGJKTk5kzZw4JCQl06dKFn376ydrJ+MyZM9YJpgDefvttCgsLueOOO2yuM3fuXObNm1eboVdKZoptcuOWfwG3NpFOisY+TiVns+bPODQKjO3VjHZhRc1r8dnx/BL3C1vObOHPxD8xq2brOe4u7vQK7UWf0D70CetDY0Nj1q9fz8gomTNCCCGEfTk9uQGYNm1auc1QW7dutdk+ffq04wOyo6wLJSbwuzjHzdWsd8tG3NgplB8PxjPnh53833UX+CH2Bw4mH7Q5LsIvggFNBnBt42vpGNgRV82lJEZGHAghhHCUOpHc1FeF+Sbysmw/xA35KVd9clNoLuTazufYmvYRR3UxPL+7aGi2gkLXoK4MCh/EoKaDaOrd1MmRCiGEaIgkuXGgkjMTA7iZMtG3aF77wdjB2ayzfHnsS7458Q2p+aloLnZxUgqbMK3naG6PHEWAIcC5QQohhGjwJLlxoJKdiXUFGbg3a4Ki0zkpoqpTVZXfz/3OZ0c/Y9u5bdbF0oLcgxjZ/Ca+2xbCPwnexDYKJ6CLJDZCCCGcT5IbByq1YGb+BfSRV0dnYqPFyE+xP/HB4Q84kX5pnp4+oX0Y03YM/Zv0x0XjwrWNLjDm3Z1sik7kyby2+Bikc7AQQgjnkuTGgbJSyl4wsy7LN+Wz9vhaVv29ivicoklo3F3c+b82/8eYyDE0825mc3zvlo14eXRnbmgbLImNEEKIOkGSGwfKLDVSKgV9m95OiqZiRouRr49/zTsH3iEpLwkAfzd//h31b0ZHjsZH71Puubd3a1JbYQohhBBXJMmNA5Wc48aQdwG3OlZzY1EtrItdx5v73uRs9lkAQj1CmdJxCje3uhk3l7LX7CqLqqr8769ztAz0oGu4n6NCFkIIISokyY2DqKpaqubGnRxcQkOdFFFp+5P2s2j3Io5cOAIU1dTc2+le7mxzJzpt1Ts9r9x2mgU/HKFlgAc/zrgOg05r75CFEEKIK5LkxkEKck0Y8802+7xDvOrEgo/Jucm8svcVvj/1PQCerp5M7jiZsW3H4u5a/ZXS/69bE9757SSnUnJY/NNR5t3c3l4hCyGEEJWmufIhojpKzXGjWvBpFuScYC6yqBY+if6Em76+ie9PfY+Cwm2tb+P7275nSscpNUpsAHzcXXnxjs4AfLj9NL8eS7ZH2EIIIUSVSHLjIFmptsmNviAdQ0RLJ0UDsRmxTPxpIi/sfoFcUy6dAjrx6Y2fsqDfArtOvNe/TSDjrikaUTVzzX4SM0tPZCiEEEI4kiQ3DlIyuXErSEPXqlWtx2G2mPng8Afc8d0d7Evah7uLO0/3fpqPRn5Eh4AODrnnf2+MIirUmws5hcz4bB8ms8Uh9xFCCCHKIsmNg5RKbvJT0ddycpOQk8CUn6fwyt5XKLQU0i+sH9/c8g1j2o5BozjuS+/mquXNsV3x0GnZfTqV3adTHXYvIYQQoiTpUOwg2SWTG1Mmro0b19r9N5/ZzNztc8koyMDdxZ0nez3Jra1vrbUOzS0DPVk6ujPebq70bSXLMgghhKg9ktw4SMkOxR6eGhSt44dGG81Glvy5hM+OfgZA+0btefH6Fwn3Dnf4vUsa3qHuDHsXQgjRcEizlINkpRXYbHsHeTr8nil5KUz5eYo1sZnYfiIfjfjIKYlNSbEpOdz30Z9k5RudHYoQQoh6TmpuHMBktJCXWWizz6eZY5tm/k75m4e2PERibiKerp4sum4RA5oOcOg9K8tiUXng470cTcjCaN7Pe+N7ODskIYQQ9ZjU3DhATolaGwDfNk0ddr+fTv/EhJ8mkJibSHPv5nxy4yd1JrEB0GgUXryjE3oXDb8cTeLFn446OyQhhBD1mCQ3DpCdZtvfxsWYi1eUY0ZKrf57NY/9+hgF5gL6N+nPpzd+Sksf582nU55OTXx58Y5OALzz2ylW7zzj5IiEEELUV5LcOEBWqm3NjVtBKrpw+/Z7sagWXtzzIkv+XALAXW3v4rWBr+Gl87Lrfezpli6NmTmkaOHQ59YdZd8F5y9FIYQQov6R5MYBsks0Sxm0BSiurna7vtFi5Mnfn+SjIx8B8Ej3R5jdazZaTd1fqHL6oNaMu6YZqgofHdfw5z9pzg5JCCFEPSMdih0gu0TNjaeH/WoojBYjT/z2BBv/2YiL4sKz1z7LTS1vstv1HU1RFObd3J6kzDxiziTSKtDD2SEJIYSoZyS5cYCSfW68Agx2ua7RbGTWr7P4Je4XXDWuvDLgFfo37W+Xa9cmrUZh6R0dWf/Tefzcdc4ORwghRD0jzVIOULLmxrtJoxpf02g2MnPrTH6J+wWdRserA1+9KhObYnpXLbrLWtE+3BbL4XMZzgtICCFEvSHJjZ2pKmSn2yY3fq1rNlOv2WLmqT+eYuvZrei1el4f9DrXN7m+RtesS77ed5Z53x/h7hW7JMERQghRY5Lc2JmlQMFiUm32+UU1q/b1VFXl+V3P89Ppn3DRuPDqwFfp17hfTcOsUwZHBdM13JeMPCP/encnO05ecHZIQgghrmKS3NiZKd+287CimvEM9qn29ZbtX8YXx75AQWHRtYu4tvG1NQ2xzvFyc2X1Pb24pqU/2QUmJqzczYa/E5wdlhBCiKuUJDd2Zs6zLVIDuSia6o2W+iLmC949+C4AT1/zNMNbDK9xfHWVl5srH07qxdB2wRSaLDzw8V7W7JGJ/oQQQlSdJDd2Zs6zTWTc9eZqXWfH+R08v+t5AP7T5T+Mjhxd49jqOjdXLW/d3Y07uzfBosITaw9xNCHT2WEJIYS4yshQcDsz59vmi14+VZ+871TGKR7d+ihm1cyolqO4r9N99gqvznPRanjxjk6E+LjhqtXQNsTb2SEJIYS4ykhyY2emEjU3XkGeVTo/PT+daZunkWXMoktgF+b1nYeiNKxlChRF4dGhkTb7EjLyMZotNPV3d1JUQgghrhbSLGVn5gLbIvUOD6z8uRYzT/z+BHFZcYR5hPHqwFfRaWWSu9xCE1NW7+HG13/nZ+loLIQQ4gokubEzc4nRUt7Ngyp97ruH3mX7+e24ad14fdDrNDLUfPK/+iC7wISrVkNmvol7P9rLcz8cwWi2ODssIYQQdZQkN3ZkMVuwFJRolmpUuaUXtp/fztv73waKRkZF+kde4YyGI8jLjTX39mHKtS0AWPFHLKPf2cHplBwnRyaEEKIukuTGjnIzCgHb5MbDV3/F8xJzEnnytydRUfm/iP/jlta3OCjCq5fORcPTN7XjnXHd8XJzYd+ZdEa89jsf7TiNxaJe+QJCCCEaDElu7Cgno9BmW6NYcPOoeLSURbXw1B9PkVaQRlv/tjzZ60lHhnjVG9Y+hPUPXUeflo3IM5r5et85JLURQghxORktZUc5JdaUcndTrzjS6eMjH7M7YTcGFwNLrl+Cm4ubI0OsF5r4ufPJlN6s3nGa/pFBaC9OkphvNOOiUXDRSs4uhBANmXwK2FFOum3NjYdPxSOdjqcd57W/XgNgVo9ZNPdp7qjQ6h2NRmFivxa0CPCw7lv801FGLdvGX2fSnBiZEEIIZ5Pkxo5K1tx4BXmVe2yhuZDZv8+m0FLI9U2u5842dzo6vHotK9/Id/vPEx2fyf+9vZ0nvjpIUma+s8MSQgjhBJLc2FHJmhvP4PKTm3cPvktMWgx+ej/m953f4CbqszcvN1d+fuR67ujeBFWFNX/G0X/JVl7eeIzsApOzwxNCCFGLJLmxo5I1N56+ZfefOZ52nPcPvQ8UDfsOMAQ4PLaGoJGnnpfu7MzaB/rQLdyXPKOZ1zcfZ8CSrew5ners8IQQQtQSSW7sqORoKU+/0sPAzRYz87bPw6SaGNR0EEOaDamt8BqM7s38WftAX96+uxvNG7lTYDTT8rK+OUIIIeo3GS1lJ6qqkpNhW3NT1hw3n8d8zsGUg3i6evJU76ekOcpBFEVhRMdQbogKJiYhi0aeRV8LVVWZ9tk+ujb15V+9wvHUy4+AEELUN/Kb3U4K80xYTLYzrriXGC2VkJNgHR31SPdHCPYIrrX4Giqdi4aOTXys27tjU/nxYDw/HozntU3HGd2zKRP7NpcFOYUQoh6RZik7yS1RawPg7mWb3CzZs4Q8Ux5dg7pyR5s7ais0cZmu4X4sur0jLQM8yCow8f4fsfRfsoV7V//JthMpMtuxEELUA5Lc2EnemRibbVedgotOa93ek7CHn//5GY2i4b+9/4tGkaJ3Bp2Lhrt6hbNpZn9WTurJdREBWFT4+Ugid6/YxbaTKc4OUQghRA1Js5Sd5BUagAzrtsH7Un8bk8XEC7tfAODONnfKoph1gEajMDAyiIGRQRxPzGLVjtPsjk2lb6tLI9e++DMOraIwpH0w3m4VL6MhhBCi7pDkxk7yCm07D7t7X2qS+urYVxxLO4a3zptpXabVdmjiCiKCvXju1o6o6qXlMoxmCy/+FENKdgG6/2noHxnITZ1CGRwVjId0QhZCiDpNfkvbSW6u7agnw8X+NhkFGSzbvwyAaV2n4evmW9uhiUq6fORaocnCv68J54eD8ZxIymbjkUQ2HklE76Lh2tYB/F/3JozsGOrEaIUQQpRHOn7YSV620Wa7OLlZcWgFGQUZtPZtLUssXEU89C48PLgNGx+5np8evo7pg1rTIsCDApOFzUeT2HfZ+lUFJjM7T10g32h2YsRCCCGKSc2NneRl2U7gZ/ByJSEngU+jPwWKhn67aKS4rzaKotA2xJu2Id7MHNKGowlZ/HI0iesjAq3H7DqVyvgPdqN30dAt3I8+rRpxTctGdG7qg95FW8HVhRBCOIJ82tpJfk6JmhtPHW/tf4tCSyHdg7tzXePrnBSZsBdFUYgK9SYq1Ntmf3JWAQGeelKyC9hx6gI7Tl0AQO+ioWNjH56+qR1dmvo6IWIhxP+3d+/RTdX53sffO/deQlvonUIpUKhyqYC2FhUdWrkoHBhHRI8HwRnwiKACjkfwUVDnecTRpUtFR9bochzXIDAyAkctCHLzhmC5VW4VailCb1DovWnS5Pf8kTZtaApVgXTC97XWNsnOJzvf/PKj/br3biKuTNLcXCT2eu9DEhXqDGvz1wLuvTbyScSB63fDErhjaHfyT9Wy/cdyvv2xnB0/lnO6xk5O4VmCW30kwL92neCzAyUMiA/jqjgrV8V1oXt4EDqdzA8hhLhYpLm5SOw272+e3lC0DpdyMbLHSFKjUv1UlbhcNE2jb3QofaNDmXJ9Ikopfjxdy97jFfSJCvXkvjxyig0HS9lwsNSzLtRsoH+slZRYK/8zOoWwYPmzcyGE+DWkublI7DbvPTe7zn6HLlzHo0Me9lNFwp80TaNPVKhXYwPw+xuTGNg9jEPF1RwqruJoWQ01DY3sKjzL7uNneXrc1Z7sorX7+fbHMyR2C8JVoaN210mSoqx0Dw8iNsyCySB/DyCEEL5Ic3OR2Ou999w49DbGVVfR+43hEJbgXsJ7QFgP6JsFCde6g0qBHLK6YgxOCGdwQrjntsPpouB0LYeKqzhxth6LseUQ1qHiavJK3Qvo+HzNAc99ep3GoefGeBqcT3KLOFNrJ9pqIcpqJtpqJspq9tqeEEJcKTpFc/Pmm2/y0ksvUVJSQmpqKkuWLCEtLa3d/IcffsjTTz/NsWPHSE5O5s9//jO33XbbZazYm7PRhdPh8lrn0NuYXlEPzgY4k+9emplCW5qbk7vh/QlgjYHQ1ks0WGMh4TqITHZnXS53IyTNUMAw6nX0i7HSL8ba5r5XJqdytKyGo6VVbNt1CFdoFEWVNk5W1BMWZPTac/OPbwv59sczbbbRxWIgNszC+kdHeM7rWb+/mDO1DiKCjYQFG4kINhERbCI82CjNkBAiIPi9uVm5ciXz5s1j6dKlpKen8+qrrzJ69Gjy8vKIjo5uk//mm2+45557WLx4MePGjeODDz5g4sSJ7N69m4EDB/rhFYDD1vbzTW5IGk7SrZ9B1QmobFoqfoLKn6D70JZgTQnYq6G8GsqPtt346MUtzc2JnfDeOAiKgOCu7sugrhDcdJlyO/S83p21VULRXjBbwdyl6dIKxiBpjv5NJEQEkxARzA29I4g6e4DbbhuG0WhEKUXVOXsKb+wbSReLkbLqBk41LXaniypbIyaDw+uE5b99fYwdBW0bIQCr2UDuM6M8J8Av2XSEI2U1hFoMWM0GQswGQs0GQi3uy7EDYz3Zijo7GhoWkw6TXicn0Qsh/Mbvzc0rr7zCjBkzuP/++wFYunQpn376Ke+++y7z589vk3/ttdcYM2YMjz/+OAB/+tOf2LhxI2+88QZLly69rLU3O/dkYoD7hvwX6A0Q0cu9tKdPJszOgZpS91Jd2nK9phSi+rVk686AywG1Ze7lXGEJLc1N6UF4/z/aZjS9u8m5ZQFc/6B7XXk+rHvC3fh4lmD3pSEIet0IiRnubEM1FH4DeiPozaA3gcHkvtSbWpoucB9yczWCziAN1UWkaVqbk45nj0z2ut3cAJ2qsVHT4N18pyd1xWoxUlFnp6Le4b6sc9DoUpiN3k3J1/mnfe4RAjDpddz2/8Z6bv/xw1w+P1TaVCMEGfVYjHqCjHrMRh0b5ozAoHfvbfrrF/nsO1GJxaDHYtRhMeox6nWY9BpGvY7/vrmPZ8/UzoIznDhbh1Gvw6jXYTbomq5rGJv+3N7YtN3yWjvlNiiutGExOdHpNAw6zXNpMejlL9OEuAL4tbmx2+3s2rWLBQsWeNbpdDqysrLYvn27z8ds376defPmea0bPXo0a9asuZSlnte5zY3SFCnR/dpJn8Noce+ZiUy+cLZvFsw94G5y6s9C/Zmm62eg7izEtfqrLE0HUSnuZqShBhqqAAXKCbYK7+3WnoKjG9t/3t/8n5bm5mwhfHBX+9kb5sCtzzZlC+D1IYDW1ASZPU2RQW+kX9B1QNPhxNrTsGySuxHSGUCnb1oM7oasbxakP+DO2uvgk7mtcuc8Ju4aGHSnO+tywhcvucdD05oude6aNB106+Pe49Vs59st4+dZmrLWOOib2ZI9uNa9/dbbbd52cNeWRhOg4AtobPqgR83zH/djTVbocV1L9qed4Kj33K85nXSrPoRWGAYWKyQMa8kW7fXKNj+BpmmE6Y2ExQ9pyZYdBnst8wYAAzTAAloQAErTUxNxFbXNjVB5PthreXSAjck99NTZXdTZG6m1O6l1KI6qhJbtVvwE9hq61eWTrFW0rHe4lyOqOwadzt3YVJ6AhmpO/nCAH/LLOVe+iseFjhkjekNVMdgq2fzlYU/T1NoxFUsjBvY8fSsRrrNgq2DZZ4fJPlDKsr3LvbLHVQwODHwzfyTxhhqoP8NbW/NZu/ckOp2GXqOpAdJRrMXg0ptZ+d/Xk2ixQV05q3af4ON9Reg0DQ3Qae638JQ+hkadmdfuHkLfUDvUlbP+QAmf7CtC0zR0rd7mCn00dr2FReMH0D/MCbWn+OroKT7NLUZr2m7zYyoNUTgMQcz+TTJXdwVqyth9/Czr9hd7XpPWNIeqDV1p0Idw/w1JDIrSQXUp+4sq+Xhfsde00IAaQwQNhlDuTuvJoG4aIbYSjhzax6f7W8a3OV9riMCmt/LbId1JSwiCqiIKz9Tyr90n29RgM3Sh3tCFMQNjGd4zFKpOUlRhY9WuE7QKA9Bg6EK9IYzfpERxU1IYVJ3gVLWdld8db/Me2/Sh1BvDuaFvN0Ymd4PK45yts7Ps27bZBn0IdcYI0pK6MvqqKKgopLqhkfe/PtYma9cHU2vsyjU9wxk3KA7OFtDQ6OKdL370kQ2i1tiNlJgQjABnC3DqDCzd2nZPu0NnpsYURb9YK3dd2wPOFACKt7bl43Ipr6xTZ6LaFE2vyBDuTU90/2xVTt7+sgB7o/f/kDg1I9XmGLqHBzHthiSoOA6uRt77upBau/dnrLk0A1XmWGK6WJh+U2/3vzmnnX/sKKSyzjurND2V5jgiQkw8dEtfqDwJzgZWfvcT5bX2c7I6Ks3xhJoNPJKZ7P732VjPR3tOUlJp88pGh3fB33/z6dfm5vTp0zidTmJiYrzWx8TEcPjwYZ+PKSkp8ZkvKSnxmW9oaKChocFzu6qqCgCHw4HD4fD5mJ+rrrrB67bBrKOxse3enF9Pg+AY99Ke5tcUNxQe+KplvXKBo66l2Qnu2pK19kAbtwTNUQ+N9e5flk2XmqMeV/RAVHPWpdDHpqK5HOC0u39hO+3uPUpOOy69BVdztqG+aYIr97lHzpZx0gCj8aqW98BWg7Fod7svyxka07JdWw3G3BXtZl0D78SZMsF9o7EB49bF7Wf7346zzyjPbcO6J9CU769RcPX+Dc7EES3ZNQ+h2Wt8ZxPScU79tCW76g9ovva2ASpmEI3Tt7Rk/zUDreJYy23gRoCjoLr2oXHmjlY1zEQrO+h7u9Z4Gh/J9dzWr3kIXdEun1ks4VgeO4olWI/D4UD/8aPojn1Jhq/t6k00zi8C3P+O9J8+hu7IZ/wZwNw2v2tKHnalc2c/ewrdwdU82072/w5cTzXBaC4nrk1/QrdvGfOB+T6ydwb/jVJlRVNOnNteQp/zNo8Bj/nI3tzwCoUqFpezEefOJei/eY2ZwMxzfwK7YEzDCxxWPXE4GnHmvo1+22LuBO70MRZ3NDzDPtWPWlsDzh/+gf7zhYwBxvjI3mtfwDeuQVTU2nAWrkG/7o/cSNN7e47p9sf43DWMSUO7069kE4b/fYihwFAf2Ufss/lf13CyUqK46uxODP+axkDA10H6Jxwz+KfzN6T3iuDq6u/JOvQ/cAiu9pF9xnEfy51jGBAXylB1AMP740gE5vnIvuiYzPvOCSSEW7jOeAzju5nEA4/4yC5pnMibjXcRHqTneuspjEsziAJ8faXwO41jeaNxCiYd3BRlw7hkCBHtZD9oHMmTjdNpdDoZ2UOH8fUhWIFZPrKrnTcw1zGLu4Z1Z3RyF4yvD8HcTna98zoedMzl9oExjLKC4a3r0ZTTZ/YL5yDucywgKyWK36bGYlh6I5q9hpk+st+5+jHJ/gzD+3TlrqHxGN7JQqstY4aP7H5XL8bZn2doz3DuTUvA8Pf/QDtbwDQf2XxXHJn2l0mJtTL1+h4Ylk1CKzvIf/nIFquuZDS8QWLXYGbckIj+n/ehO5nDZB/ZChXCNQ1vE2M1M3NEL/QfPYDu2Bfc4SP7vWkIPw6Ye9F+xzb7Odvz+2GpS23x4sU8++yzbdZv2LCB4ODgi/Ic9WV6oPW2nGRnZ1+UbV8+YU3LOTTgBwf80Or1xD3W/maqgebXrlwYB/0FnWp0L67GluuqkQZDGAc2uvcY6Vx2onrPRVMuNFxoyommXOiUCw0nNTWxnGnart7VQFL85DbZ5uuV1VGcbMpqqpFBkSNBKTTcC8rlvkRRWRPOj63eq2vDhrXJaKopW2vlcKtsuqUPepMdDRco3M+PAqWoqg9mX6tshi4aU1AwNG2zeWgBqhuC2dUqe72zC0GWBE/OnXVfr20MZUfrGmwmQs2tml3Vsm2bK4SvWmXTaiHMFOnJtK7DQRBbWo9DRQPdDOFeNTRfV5qeDa2yQ09XE21oe0J0s5Pff4PS9GQfgNTSs8SdJztEV0ijPoj1648xsOgUCefJTu9dQ4NRz7ZNG7iqqJhEfWi72QWpLqpMjXz35WZSSn+ijz6k1Tvh/TKn9nNRbmpk3/at2E4do58+BBfNw+Z9SGtCkkaaycnh776Cs0e5Sh+CS3mPWrOs7hp9LE6O7vkGY1UeA5uyLh/h62M0wi1OCr/fQWjdAVL1we1mr4nS0CxOTh7KIce+j2FNWaeP7ICuOsYFOTl1ZA+7nAdIO0+2f4SO24KcVPyYyzcFR8jQBaHwnU0K0zM6yEXdTwf4qqiQG3WWdrM9rHqygl3Yi/LYVl7Mzc1ZV9tsXKiBzGAX6tRRNm8uZ6TOAkCjj2x0iIHMEBemMwVs3JjLrefJdgt2Z0Oqj7N+/VHGnCcbHmQkM8pFZEMRWN17ZzTl8pkNtZjIjHIR4yghOzubUcqIQWfxmQ02mciMdBGpTpGdnU1mo4ZZZ6HRa2K6mZqyEfpysrOzucXmJLidrMHoznYxVZCdnc1NNQ1Y28miNzMy3kWIoZrs7GyGV9YRrrPgVK1+TDRp1FsYGe/Coq8jOzubtDPVRLaTbT70u3HjeY4I/AJ1dXUdzmpKnVvW5WO32wkODmbVqlVMnDjRs37q1KlUVFSwdu3aNo/p2bMn8+bNY86cOZ51ixYtYs2aNezbt69N3teemx49enD69Gm6dOnSJv9LHNt3mq3LjuCwNaIURMQFM+nJYRd+4BXM4XCwceNGbr31VoxGf+/A7NxkrDpOxqrjZKx+HhmvjrtUY1VVVUVkZCSVlZUX/P3t1z03JpOJYcOGsWnTJk9z43K52LRpE7Nn+9rxCBkZGWzatMmrudm4cSMZGb52oIPZbMZsbruf2mg0XrRBT742juRr47Db7Xz68TqyMq+Xyd9BF/N9CHQyVh0nY9VxMlY/j4xXx13ssfo52/L7Yal58+YxdepUrr32WtLS0nj11Vepra31/PXUfffdR/fu3Vm82H3exKOPPsrNN9/Myy+/zO23386KFSvIycnhr3/9qz9fBtB0MqABLCEy8YUQQgh/8XtzM3nyZE6dOsXChQspKSnhmmuuYf369Z6Tho8fP45O1/JhZcOHD+eDDz7gqaee4sknnyQ5OZk1a9b47TNuhBBCCNG5+L25AZg9e3a7h6G2bt3aZt2kSZOYNGnSJa5KCCGEEP+O5Jv3hBBCCBFQpLkRQgghRECR5kYIIYQQAUWaGyGEEEIEFGluhBBCCBFQpLkRQgghRECR5kYIIYQQAUWaGyGEEEIEFGluhBBCCBFQpLkRQgghREDpFF+/cDkppQD3V6dfbA6Hg7q6OqqqquRbYy9AxqrjZKw6Tsaq42Ssfh4Zr467VGPV/Hu7+ff4+VxxzU11dTUAPXr08HMlQgghhPi5qqurCQsLO29GUx1pgQKIy+WiqKgIq9WKpmkXddtVVVX06NGDn376iS5dulzUbQcaGauOk7HqOBmrjpOx+nlkvDruUo2VUorq6mri4+PR6c5/Vs0Vt+dGp9ORkJBwSZ+jS5cuMvk7SMaq42SsOk7GquNkrH4eGa+OuxRjdaE9Ns3khGIhhBBCBBRpboQQQggRUKS5uYjMZjOLFi3CbDb7u5ROT8aq42SsOk7GquNkrH4eGa+O6wxjdcWdUCyEEEKIwCZ7boQQQggRUKS5EUIIIURAkeZGCCGEEAFFmpuL5M0336RXr15YLBbS09PZuXOnv0vqlJ555hk0TfNaUlJS/F1Wp/DFF18wfvx44uPj0TSNNWvWeN2vlGLhwoXExcURFBREVlYWR44c8U+xfnahsZo2bVqbeTZmzBj/FOtnixcv5rrrrsNqtRIdHc3EiRPJy8vzythsNmbNmkW3bt0IDQ3ld7/7HaWlpX6q2H86Mla33HJLm7n14IMP+qli/3nrrbcYPHiw57NsMjIyWLduned+f88paW4ugpUrVzJv3jwWLVrE7t27SU1NZfTo0ZSVlfm7tE5pwIABFBcXe5avvvrK3yV1CrW1taSmpvLmm2/6vP/FF1/k9ddfZ+nSpezYsYOQkBBGjx6NzWa7zJX634XGCmDMmDFe82z58uWXscLOY9u2bcyaNYtvv/2WjRs34nA4GDVqFLW1tZ7M3Llz+fjjj/nwww/Ztm0bRUVF3HHHHX6s2j86MlYAM2bM8JpbL774op8q9p+EhAReeOEFdu3aRU5ODiNHjmTChAkcOHAA6ARzSolfLS0tTc2aNctz2+l0qvj4eLV48WI/VtU5LVq0SKWmpvq7jE4PUKtXr/bcdrlcKjY2Vr300kuedRUVFcpsNqvly5f7ocLO49yxUkqpqVOnqgkTJvilns6urKxMAWrbtm1KKfc8MhqN6sMPP/RkDh06pAC1fft2f5XZKZw7VkopdfPNN6tHH33Uf0V1YhEREeqdd97pFHNK9tz8Sna7nV27dpGVleVZp9PpyMrKYvv27X6srPM6cuQI8fHx9O7dm3vvvZfjx4/7u6ROr6CggJKSEq95FhYWRnp6usyzdmzdupXo6Gj69+/PzJkzKS8v93dJnUJlZSUAXbt2BWDXrl04HA6vuZWSkkLPnj2v+Ll17lg1W7ZsGZGRkQwcOJAFCxZQV1fnj/I6DafTyYoVK6itrSUjI6NTzKkr7rulLrbTp0/jdDqJiYnxWh8TE8Phw4f9VFXnlZ6eznvvvUf//v0pLi7m2Wef5aabbmL//v1YrVZ/l9dplZSUAPicZ833iRZjxozhjjvuICkpifz8fJ588knGjh3L9u3b0ev1/i7Pb1wuF3PmzOGGG25g4MCBgHtumUwmwsPDvbJX+tzyNVYA//mf/0liYiLx8fHk5ubyxBNPkJeXx0cffeTHav3j+++/JyMjA5vNRmhoKKtXr+bqq69m7969fp9T0tyIy2rs2LGe64MHDyY9PZ3ExET++c9/8oc//MGPlYlAcvfdd3uuDxo0iMGDB9OnTx+2bt1KZmamHyvzr1mzZrF//345z60D2hurBx54wHN90KBBxMXFkZmZSX5+Pn369LncZfpV//792bt3L5WVlaxatYqpU6eybds2f5cFyAnFv1pkZCR6vb7NWeClpaXExsb6qap/H+Hh4fTr14+jR4/6u5ROrXkuyTz7ZXr37k1kZOQVPc9mz57NJ598wpYtW0hISPCsj42NxW63U1FR4ZW/kudWe2PlS3p6OsAVObdMJhN9+/Zl2LBhLF68mNTUVF577bVOMaekufmVTCYTw4YNY9OmTZ51LpeLTZs2kZGR4cfK/j3U1NSQn59PXFycv0vp1JKSkoiNjfWaZ1VVVezYsUPmWQecOHGC8vLyK3KeKaWYPXs2q1evZvPmzSQlJXndP2zYMIxGo9fcysvL4/jx41fc3LrQWPmyd+9egCtybp3L5XLR0NDQOebUZTltOcCtWLFCmc1m9d5776mDBw+qBx54QIWHh6uSkhJ/l9bpPPbYY2rr1q2qoKBAff311yorK0tFRkaqsrIyf5fmd9XV1WrPnj1qz549ClCvvPKK2rNnjyosLFRKKfXCCy+o8PBwtXbtWpWbm6smTJigkpKSVH19vZ8rv/zON1bV1dXqj3/8o9q+fbsqKChQn3/+uRo6dKhKTk5WNpvN36VfdjNnzlRhYWFq69atqri42LPU1dV5Mg8++KDq2bOn2rx5s8rJyVEZGRkqIyPDj1X7x4XG6ujRo+q5555TOTk5qqCgQK1du1b17t1bjRgxws+VX37z589X27ZtUwUFBSo3N1fNnz9faZqmNmzYoJTy/5yS5uYiWbJkierZs6cymUwqLS1Nffvtt/4uqVOaPHmyiouLUyaTSXXv3l1NnjxZHT161N9ldQpbtmxRQJtl6tSpSin3n4M//fTTKiYmRpnNZpWZmany8vL8W7SfnG+s6urq1KhRo1RUVJQyGo0qMTFRzZgx44r9nw1f4wSov/3tb55MfX29euihh1RERIQKDg5Wv/3tb1VxcbH/ivaTC43V8ePH1YgRI1TXrl2V2WxWffv2VY8//riqrKz0b+F+8Pvf/14lJiYqk8mkoqKiVGZmpqexUcr/c0q+FVwIIYQQAUXOuRFCCCFEQJHmRgghhBABRZobIYQQQgQUaW6EEEIIEVCkuRFCCCFEQJHmRgghhBABRZobIYQQQgQUaW6EEEIIEVCkuRFCCCFEQJHmRgjhd9OmTWPixIl+e/4pU6bw/PPPdyh799138/LLL1/iioQQv4Z8/YIQ4pLSNO289y9atIi5c+eilCI8PPzyFNXKvn37GDlyJIWFhYSGhl4wv3//fkaMGEFBQQFhYWGXoUIhxM8lzY0Q4pIqKSnxXF+5ciULFy4kLy/Psy40NLRDTcWlMn36dAwGA0uXLu3wY6677jqmTZvGrFmzLmFlQohfSg5LCSEuqdjYWM8SFhaGpmle60JDQ9sclrrlllt4+OGHmTNnDhEREcTExPD2229TW1vL/fffj9VqpW/fvqxbt87rufbv38/YsWMJDQ0lJiaGKVOmcPr06XZrczqdrFq1ivHjx3ut/8tf/kJycjIWi4WYmBjuvPNOr/vHjx/PihUrfv3gCCEuCWluhBCd0t///nciIyPZuXMnDz/8MDNnzmTSpEkMHz6c3bt3M2rUKKZMmUJdXR0AFRUVjBw5kiFDhpCTk8P69espLS3lrrvuavc5cnNzqays5Nprr/Wsy8nJ4ZFHHuG5554jLy+P9evXM2LECK/HpaWlsXPnThoaGi7NixdC/CrS3AghOqXU1FSeeuopkpOTWbBgARaLhcjISGbMmEFycjILFy6kvLyc3NxcAN544w2GDBnC888/T0pKCkOGDOHdd99ly5Yt/PDDDz6fo7CwEL1eT3R0tGfd8ePHCQkJYdy4cSQmJjJkyBAeeeQRr8fFx8djt9u9DrkJIToPaW6EEJ3S4MGDPdf1ej3dunVj0KBBnnUxMTEAlJWVAe4Tg7ds2eI5hyc0NJSUlBQA8vPzfT5HfX09ZrPZ66TnW2+9lcTERHr37s2UKVNYtmyZZ+9Qs6CgIIA264UQnYM0N0KITsloNHrd1jTNa11zQ+JyuQCoqalh/Pjx7N2712s5cuRIm8NKzSIjI6mrq8Nut3vWWa1Wdu/ezfLly4mLi2PhwoWkpqZSUVHhyZw5cwaAqKioi/JahRAXlzQ3QoiAMHToUA4cOECvXr3o27ev1xISEuLzMddccw0ABw8e9FpvMBjIysrixRdfJDc3l2PHjrF582bP/fv37ychIYHIyMhL9nqEEL+cNDdCiIAwa9Yszpw5wz333MN3331Hfn4+n332Gffffz9Op9PnY6Kiohg6dChfffWVZ90nn3zC66+/zt69eyksLOT999/H5XLRv39/T+bLL79k1KhRl/w1CSF+GWluhBABIT4+nq+//hqn08moUaMYNGgQc+bMITw8HJ2u/R9106dPZ9myZZ7b4eHhfPTRR4wcOZKrrrqKpUuXsnz5cgYMGACAzWZjzZo1zJgx45K/JiHELyMf4ieEuKLV19fTv39/Vq5cSUZGxgXzb731FqtXr2bDhg2XoTohxC8he26EEFe0oKAg3n///fN+2F9rRqORJUuWXOKqhBC/huy5EUIIIURAkT03QgghhAgo0twIIYQQIqBIcyOEEEKIgCLNjRBCCCECijQ3QgghhAgo0twIIYQQIqBIcyOEEEKIgCLNjRBCCCECijQ3QgghhAgo/x+3SLf9WOua/gAAAABJRU5ErkJggg=="]},"metadata":{}}],"source":["# Plot the concentrations over time\n","#plt.plot(t, P, label='Protein')\n","plt.plot(t, L1, linestyle='--', label='Ligand1')\n","plt.plot(t, L2, linestyle='--', label='Ligand2')\n","plt.plot(t, PL1, label='Protein-Ligand1 Complex')\n","plt.plot(t, PL2, label='Protein-Ligand2 Complex')\n","plt.plot(t, PL1+PL2, linewidth=3, label='Protein-Ligand Complex')\n","\n","plt.xlabel('Time (s)')\n","plt.ylabel('Conc. (M)')\n","plt.grid()\n","plt.legend()\n","plt.show()"],"metadata":{}},{"id":"4f318e6a-0102-44b4-9d4b-f97a0b40d80d","cell_type":"markdown","source":["notice how the Protein-Ligand2 complex (red) ends up being higher than the Protein-Ligand1 complex (green), even though tautomer 1 is ~19X more abundant! This is because tautomer 1 is much less potent, so it's bound fraction is smaller. \n","\n","but what we really care about is the total amount of complexed protein in purple, which is the sum of PL1 and PL2, because that's what we would observe experimentally. That is, the purple line is how we calculate our observed, Kd in the lab. In lieu of doing the IRL experiment, we can infer the on- and off-rates in reverse, kind of like if this was an SPR sensorgram. Then we find our observed K_eq as `observed on-rate / observed off-rate`.\n","\n","Practically, this is achieved by fitting an ODE model with scipy.optimize to the purple curve. We change the ODE to assume there is a single ligand species, because in experiment we can only observe a single readout, and wouldn't know the concentrations of each ligand species i.e. the we fit an ODE model that assumes `P+L<->PL`. This resembles what people do every day when screening compounds that might have tautomers or protonation states or, indeed, proteins with more than one conformation. We always just assume it's a single protein and single ligand, and we always measure the 'observed' equilibrium state, which is a smoosh of all binding modes, protomers and conformations. "],"metadata":{},"attachments":{}},{"id":"3e99902f-29db-4fe1-aaa7-8c0a9e4653bb","cell_type":"code","execution_count":8,"outputs":[],"source":["# the ODE for our single-protein, single-ligand model (P+L<->PL)\n","def rate_equations(y, t, k_on, k_off):\n"," P, L, PL = y # concs\n"," \n"," # rate updates:\n"," dPdt = -k_on * P * L + k_off * PL\n"," dLdt = -k_on * P * L + k_off * PL\n"," dPLdt = k_on * P * L - k_off * PL\n"," \n"," return [dPdt, dLdt, dPLdt]\n"," "],"metadata":{}},{"id":"2716d517-9633-46db-9cc9-f81868dd53ee","cell_type":"markdown","source":["and now, to fitting the observed concentration curve to estimate the correct rates, as you would do in experiment. Note that I first tried scipy.optimize.minimize but the gradient was too flat in the precision range. I found that the 'DIRECT' algorithm available in scipy.optimize finds a solution quickly, is consistent over time, and doesn't take long to complete. I guess it is gradient-free so it doesn't get stuck."],"metadata":{},"attachments":{}},{"id":"6543caba-4498-47b8-844e-53829c1886f2","cell_type":"code","execution_count":9,"outputs":[{"output_type":"execute_result","execution_count":null,"data":{"text/plain":[" message: Number of function evaluations done is larger than maxfun=5000\n"," success: False\n"," status: 1\n"," fun: 2.1740294333618713e-12\n"," x: [ 3.653e+00 -3.299e+00]\n"," nit: 271\n"," nfev: 5013"]},"metadata":{}}],"source":["#this is our target data, it's the observed \"PL\" in P+L<->PL\n","observed = np.array(PL1+PL2)\n","\n","def fitting_function(pars):\n"," \"\"\"\n"," This is a loss function for a given set of on-rate and off-rates\n"," The on-rate and off-rate are in logspace, allowing the model to fit \n"," more smoothly. So the first step is to transform back to linear space. \n"," \"\"\"\n"," k_on, k_off = pars\n"," k_on = 10**k_on # transform to linear space\n"," k_off = 10**k_off # transform to linear space\n"," #P0 = ...#already been set.\n"," PL0 = 0\n"," L0 = L1_0+L2_0 #already been set. It's the sum of equilibrated L1 and L2 populations.\n"," \n"," y0 = [P0, L0, PL0]\n"," #generate a simulated curve.\n"," y = odeint(rate_equations, y0, t, args=(k_on, k_off))\n","\n"," #see how closely this curve matches the observed data. \n"," rmse = ((y[:,-1]-observed)**2).sum()\n"," return rmse\n","\n","\n","# I put in some sensible bounds on the rates, using the sprpages graph linked above. \n","\n","res = optimize.direct(fitting_function,maxfun= 5_000,\n"," bounds=[(1,9), \n"," (-6,1)]\n"," )\n","res"],"metadata":{"scrolled":true}},{"id":"3b6eaecd-a7a6-4ce1-ba40-01233a76fe10","cell_type":"markdown","source":["OK the loss is very small, so our observed, apparent, P+L<->PL system must be pretty close to the simulated ligand species' kinetics model. \n","\n","So we can calculate the observed Kd, and this would be a reasonable simulation of our belief about the Kd in a real life experiment. \n","\n","First let's just plot the overlap of the equilibration process to make doubly sure:"],"metadata":{},"attachments":{}},{"id":"6a6fc20f-ef52-49ec-b6ef-58e0932a31bb","cell_type":"code","execution_count":10,"outputs":[{"output_type":"execute_result","execution_count":null,"data":{"text/plain":["array([ 3.6532315 , -3.29852326])"]},"metadata":{}}],"source":["res.x"],"metadata":{}},{"id":"8b7fad3a-a2a2-48d4-a137-6b1c4330d142","cell_type":"code","execution_count":11,"outputs":[{"output_type":"display_data","data":{"text/plain":["<Figure size 640x480 with 1 Axes>"],"image/png":["iVBORw0KGgoAAAANSUhEUgAAAjcAAAHACAYAAABeV0mSAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjkuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy80BEi2AAAACXBIWXMAAA9hAAAPYQGoP6dpAABk6ElEQVR4nO3deVhU9f4H8PeZYRh2UNkEQUAFcd+CME1N3DNNM0t/aW7dUisly7w3Rdssu5kt3rwtSlam3a7aLVdCUSvcRc01FUWRVWSH2c75/YFMjiwOOMOB4f16Hp6cM9/5zns+TDMfzipIkiSBiIiIyEYo5A5AREREZElsboiIiMimsLkhIiIim8LmhoiIiGwKmxsiIiKyKWxuiIiIyKawuSEiIiKbwuaGiIiIbAqbGyIiIrIpbG6IiIjIpjTp5mbv3r0YOXIk/Pz8IAgCNm/ebNXnW7x4MQRBMPlp3769VZ+TiIioqWnSzU1xcTG6du2KlStX1ttzduzYEenp6cafX3/9td6em4iIqCmwkzuAnIYNG4Zhw4ZVe79Go8E//vEPfPfdd8jLy0OnTp3w7rvvon///nV+Tjs7O/j6+tb58URERFSzJr3m5m5mz56NpKQkrF+/HidOnMC4ceMwdOhQ/Pnnn3We888//4Sfnx9CQkIwceJEpKamWjAxERERCZIkSXKHaAgEQcCmTZswevRoAEBqaipCQkKQmpoKPz8/47jo6GhERETg7bffrvVzbNu2DUVFRQgLC0N6ejqWLFmCtLQ0/PHHH3B1dbXUSyEiImrSmvRmqZqcPHkSBoMBoaGhJss1Gg1atGgBADh79izCw8NrnGf+/Pl45513AMBkE1iXLl0QGRmJ1q1b4/vvv8e0adMs/AqIiIiaJjY31SgqKoJSqcSRI0egVCpN7nNxcQEAhISE4MyZMzXOU9EIVcXDwwOhoaG4cOHCvQcmIiIiAGxuqtW9e3cYDAZkZWWhb9++VY6xt7e/p0O5i4qKcPHiRTz11FN1noOIiIhMNenmpqioyGStSUpKCpKTk9G8eXOEhoZi4sSJmDRpEt5//310794d2dnZSEhIQJcuXTBixIhaP9+8efMwcuRItG7dGtevX0dsbCyUSiWefPJJS74sIiKiJq1J71CcmJiIAQMGVFo+efJkxMXFQafT4c0338TatWuRlpYGT09P3H///ViyZAk6d+5c6+d74oknsHfvXty4cQNeXl7o06cP3nrrLbRp08YSL4eIiIjQxJsbIiIisj08zw0RERHZFDY3REREZFOa3A7Foiji+vXrcHV1hSAIcschIiIiM0iShMLCQvj5+UGhqHndTJNrbq5fv46AgAC5YxAREVEdXL16Fa1atapxTJNrbiouc3D16lW4ublZdG6dToedO3di8ODBUKlUFp3b1rBW5mOtzMdamY+1qh3Wy3zWqlVBQQECAgLMulxRk2tuKjZFubm5WaW5cXJygpubG9/8d8FamY+1Mh9rZT7WqnZYL/NZu1bm7FLCHYqJiIjIprC5ISIiIpvC5oaIiIhsCpsbIiIisilsboiIiMimsLkhIiIim8LmhoiIiGwKmxsiIiKyKWxuiIiIyKbI2tzs3bsXI0eOhJ+fHwRBwObNm+/6mMTERPTo0QNqtRpt27ZFXFyc1XMSERFR4yFrc1NcXIyuXbti5cqVZo1PSUnBiBEjMGDAACQnJ2POnDmYPn06duzYYeWkRERE1FjIem2pYcOGYdiwYWaPX7VqFYKDg/H+++8DAMLDw/Hrr7/igw8+wJAhQ6wVk4iIiBqRRnXhzKSkJERHR5ssGzJkCObMmSNPICKiBkCSJEgSIN2xzGTMHY/R6kXoxfL/ioLhjvlu/4d0+4Jbi27dVthBqriGoUEHSAZI4m1jb59M5QgJtwbrNYBBe1vGW/NWpLR3AYRbX0+6Ugj60orZTPMBkOxdISlVf43VldxZnr/Gql0Bpf1tY4urH2vvCtipb+Utg6EoF/rSfORlpcFOZVd5rMrROFYoy685g8rp1lgNhLKbpvebvDbn8loAgEELRcmNGvK6lM8NAAYdFCXZdxl768LRoh6KoswaxjpDcvC4NdYARVF69WNVTpAcm0On16NEX+2wetGompuMjAz4+PiYLPPx8UFBQQFKS0vh6OhY6TEajQYajcZ4u6CgAED5VUt1Op1F81XMZ+l5bRFrZT5br5UoStDoRZTpDSjTidAXZkOnLYNBp4VBp4FBp4VoKP+vRuGIPJd20BlE6EUJvmk7AV0pJIMWMOgg6jTQZWVgX9Z+FKlaILn5UBgkCaIooU/mWjjoCyFIBgiiAbj1XwEG3FS0wI/NnoZBlGCQJPzfjY/RzJADhWSAIInlj4EIQZKQo2iOZY4xEKXyr+95JR8iQLwGBcobAUESIUCCAAn5gitetF9ibDwW65YjXLwIQILi1hgFRAASSuGAR4UPyueVgH9iOSJxyjiXAuKt1kCCCAW6ab9ARZ/xkepjDFIcgXCrAfjrmsnltztrvoQW5Q3A+6p/YZTidzhAwmgAQnL5SIVQPrZr2WfIR/kX6tt2X2CC3a5qf3f3l32MDLQAALxm9zWm222rduxDmn/ikuQHAHjJ7ns8b7e52rEjNG/hlBQMAJip/BGvqDZUO3acZhEOSe0BAE8rt2Oxam21Yydp52Ov2BUA8LhyN5apPq927N+0c7BDjAAAPKL4HR/Zf4KxAHC28ti52uewSewLAIhWHMEX9u9XO+/fddOwzjAQANBb8QfW2b9d7dg3dBPxpWEEAKCHcB4b1YurHfu+7jF8bBgDAGgvpGK7+tVqx/5L/wiW6Z8AAAQKmdirnlvt2DX6IViinwwA8MJNHHKYVe3YDfr+mK9/BgAQ5KLEqGHW+Y41R6Nqbupi6dKlWLJkSaXlO3fuhJOTk1WeMz4+3irz2iLWynxy1sogAmV6CWWiAI0B0BoMaF5yGdCXQmEog8JQBqWhDEqxDEqDBlcEf+xW9IZWBCRRj4W6D2EvaWEPLewlLdQo/3GABr+KnfGC7nnjc51XPwX7O9YkVPjV0BGzdf8w3j6uXgR3oYq/1EuAY2JbvHA23LjoOfV/4SfkVjnvWTEA8RnDjbcX2R9GG0XVf6FeEb1xtqDIeNvf/hI6KC5XOTZbdEdaXpnxdjP7bARWM2+R5ID8sr/+3HVSFaOZsrDKsXpJAfG2v/DtoYejoK1y7J0UkGAniGaNpboxSMLdB92il2ra9fX2NlWATlJWO1K8bRdaCYC2xrGm7a9GUlU71mCya66AshrG6mH6nJb+zCopqX6t3J0E6c51lzIRBAGbNm3C6NGjqx3z4IMPokePHlixYoVx2Zo1azBnzhzk51e9GrCqNTcBAQHIycmBm5ubpeIDKO8q4+PjMWjQIKhU1b8BiLWqDUvWSm8QkVtQhIIbGSjMTcdNnRppSj/kl+qgLcpF/ysfw157E/b6ItgbSqAWS+AolcAZZfjJEGX8q8wZpTjlMK3a59lqiMBM3ZxbtyRcUv+fcc3AnfYYumCyrvyvTJVSwHG7p6ES9NBBBT3soBfsbv1XhXOq9ljp8TLsFAJUSgXm3HgdamggCiqIChVEwQ7FZRo4ubiiwCEAv/tPgVIhQCEIeOD6aqgNxYBCCUmwg6BQAoICksIOGnVzXGw1xjg2KGMb1IYSQGEHQVBCUCohKJQQFAIkOyfktnoICkGAAKBZ1kHY6YsACBAUCkBQAIIAQVBAUtqjyDeyfKwAOOWehVJfBAgKKIzjBOBWFq1XZygEQBAAVWEaFPqSW3Mqb80hQBIUUAiA6BEEAYBCABSlNyDoyyAIgFDxxXXrOQEBokvL8tsAhLI8QK+B3qDD778l4YEHHoCdSgVAAARAcmwBCIryx2qLIRjKPz9vnxe35oXatXwsBEBfBoj6W0P++vIUKh5j52CsDUQ9IBruGHsrryAAgtKYF9JfjVileSv+VfFazfk6q5hDkv76txnK/z/8BYMGRfMz6y4qajV4sGU/3wsKCuDp6Yn8/Py7fn83qjU3UVFR2Lp1q8my+Ph4REVFVfsYtVoNtVpdablKpbLaG9Sac9sa1sp8NdVKo9MjMzsbuRmpyCyRcFHviawCDTT5mRiTtgzOuly4GvLhIeXDXyiF/63HfacfgNf1MwAALijBfIetlSe/9fnvIpTAQaWAi9oOzioHZGh8oFE4Qqt0gk7pDL2dMwwqZ0DlBEePcLzeuiMc7JRQqxQ4de1tKFX2UKqdobR3hJ2DM1RqZ6gcHNHFpQVOefjBQaWEUiEAUiYgCKjqlfoBGGCyxDSvTqfD1q1bcf/w4VCpVHeMfa/G+vYxufVcjWNNtH/E/LFBfe4+poKvh/ljm7mYP9atfI21TqeD4HgGHr6ta/h/sPKm/uo51GJs5c/khk641UDZ29vzM+suKmpl6c/32swla3NTVFSECxcuGG+npKQgOTkZzZs3R2BgIBYsWIC0tDSsXVu+DfXZZ5/FJ598gldeeQVTp07Frl278P3332PLli1yvQSieqETgQtZRUjL1yItMxO+f66HfdFVuJVeQwtdBrykGwgUNAhEecOy7FbD4oxSLHVI+muiiv05oUS+4I5m7u4Y7ucLd0cV3BzssD97FgSnFrBzdofayR2OLh5wcvGAs5sHhrh7YoRzs9tSnTf/BXSbaf7YWvw1TURUFVmbm8OHD2PAgL/+toqJiQEATJ48GXFxcUhPT0dqaqrx/uDgYGzZsgVz587Fhx9+iFatWuGLL77gYeBkEyRJQnpuIa5eOoX8KychZZ+Hc8FFNC+7ghxdOIYdKP/ftXyT0B3nhrrVDxTBGV5ujhgT5A9vVwd4utgj+cZiqN284dTMF64tWsK9RUvYOXmghSBgKIChJhNVv3MjEVFjIWtz079//0qHK96uqrMP9+/fH8eOHbNiKiLrKyrT4XRqJk5m6XA+oxCXM7PxdtbzCEQG/KrYmTZHcIKzWolgT2e0btESx/NGQeHiDWWLYDh5B6OZbzDcvAPgonZBNADTEyZUfyQEEZEtalT73BA1RmU6A85d+BM3zuyDmHYMbnmnEaK/iAKxDd7QvWwc564uhEowoBQOyFK3RrFbG4ieoVB7hyLveiGOjXsI9va3ztGB6g93JSJq6tjcEFlYQZkOR67cxMGUXPRMXoSw0mPoKmSZDhKATsqrGNTOB+G+rmjn44pifAu3VkFwbB6A1rftd6LT6XB661aTI0WIiKh6bG6I7lGZVo+Txw/hxomdKMm+hHn5jxvPQfIf+xQEKLIgQsA1+xDkN+sC+4Bu8A6NhG9wN3yuuv1oFD9Z8hMR2Ro2N0R1kHotDSn7N8MuZTfaFh3GfUL5KdRFScBiaTiat/DGfUHNUeIyD1m+bvAK741AB3eZUxMRNQ1sbojMIEkSzmcWYdsf6fA89D6eKPsegRVneRUADVRIde4KXdCD+OXBB+Ht0/LWI7vKlpmIqKlic0NUg8sXz+HKnrVYeaMHDt4oP0nZOKUb/k8l4qpda9zwG4AWXYaiVZd+aGdvnct5EBFR7bC5IbpD3o1snElYC5fzm9BR9weCBAm/6iYg2e4RPNjOE33CpqEwYAYC/EMRIHdYIiKqhM0NEQBJFHFi/y8oSfoC3Qt2IUq4dfVZATiv7oxBkffjxYcGwUXN/2WIiBo6flJTk1ak0WPj0WvY+NtJbCh8GmpBDwjAZUUgckJGI2TAZIT6t5U7JhER1QKbG2qSMq6l4NDO77DgSk8UafQAFPifuh/aNFej2YN/Q3DXfgjieWWIiBolNjfUpFw7fwwZW99Fl5s7MVIw4F/apdB4dcDkqCAM7bEBrg682i8RUWPH5oaahKt/Hkfm/5agR8EutBIkQADO2HfCm0Pao8f9/Xj2XyIiG8LmhmxaZsZ1XN3wErrnbkPArabmiFMfOD0Ug/BeA+WOR0REVsDmhmxSQZkO/9p9Eet+O4d45e9QChKSnaLgOjQWPbtEyR2PiIisiM0N2RTJoMeBbWvx/LFWyC7WAbDDl55zMPqBLuh2H9fUEBE1BWxuyGZcSt4D/DwX9+sv4gHtTBz3HIK/Dw9HdPhw7lNDRNSEsLmhRq+suAAnvn4ZPdM3QClIKJCc8EhnT7w7ri/Udkq54xERUT1jc0ON2p+/b4ZL/MuIkLIAATjoGo3AJz/AQ36BckcjIiKZsLmhRqlMZ8D+uFfRP+0zAEA6PJHe9x1EDBwnczIiIpIbmxtqdC5mF+H5dcfglOGLPvYKJLUYjc6T3kcPj+ZyRyMiogaAzQ01HpKEHXt/xdyEYpRoDWju3AUHhsaj73295E5GREQNCJsbahTKivNx5t9Po0/+b/DXvQHPkK5Y8UQ3+Lg5yB2NiIgaGDY31OBlXT6F0q+fRHfDFeigxLwuGkSPj4RSwcO7iYioMjY31KD9+dtGtIyfBW+UIBseyBjybwzpPVTuWERE1ICxuaEG69jG5eh8/A3YCSL+UHZAs6fXoXNAsNyxiIiogWNzQw2OJEnY8cPnGHpqCSAAv7sOQdfn4uDs5CR3NCIiagTY3FCDIooSXv/5NL454oMvVV2AwEj0nboMCqVC7mhERNRIsLmhBkOnKUHMD6fx08lMAHa4MGg1pj3YTu5YRETUyLC5oQZBW5yHyx+PxH1FPtiunIJ/juuGUd385Y5FRESNEJsbkp2mMAdpn4xAqOYsWiod0W7kq4hiY0NERHXE5oZkpSnOQ/a/hiNEex43JVdcGvY1onrxjMNERFR3bG5INoJeg4xPR6Gt9jxyJVdcfngDet73gNyxiIiokWNzQ7KQdKUIPr0CbQ2nkC8548rwb9GDjQ0REVkAj68lWfzw4yZ00J9GkeSA0w+tRvfIfnJHIiIiG8E1N1Tvvth3CW8e98RexYt47IFOiO7HyykQEZHlsLmhehV/MhVvbT0DALBv1RP9Bg+TOREREdkabpaienN139cI+WEIWiETEyMC8JCfJHckIiKyQWxuqF7knk+Cd8JctBGuY57XQbw2PAyCIHcqIiKyRWxuyOo0eekQ10+EGjr8ZheB/n9bATteK4qIiKyE3zBkXQYdrn/+BDzFG7gEf7Sa+jXcnR3kTkVERDaMzQ1Z1cVv5yC4OBmFkiOyRqxGaz9fuSMREZGNY3NDVpP+27doc+kbAEBC+Bu4/777ZU5ERERNAQ8FJ6so0eoR87s95ophuO7eEyMfny53JCIiaiLY3JBVvLnlDJJuOOGK6xv4aUYfKBU8NIqIiOoHmxuyuN/2J2HdgVwIAvDP8T3Rws1Z7khERNSEcJ8bsqibJ3cgavswxNp9hRl9gtC7rafckYiIqInhmhuyGKk0D+LmWVBAgreTAhOGtJc7EhERNUFcc0MWk/LtHLQwZOOK5IPQSR9CbaeUOxIRETVBbG7IIvKSf0bItU0QJQHJPd5Cu1Y+ckciIqImis0N3bvSPOCnFwAAPzk+ghEPj5U3DxERNWlsbuieXf1+HjwMN5Ai+SJ0wnu8bhQREcmK30J0T/JLdfgy1Qc5khuSOi1GeCA3RxERkbx4tBTdkw/izyOuuDf2ez6IzaOj5Y5DRETENTdUd2fT8/D1/isAgNdG9YSDikdHERGR/NjcUJ1IeVfh+sUDGIIkDOvogz7teLI+IiJqGLhZiurk+n/mwd9wDTNU2+A1Yr7ccYiIiIxkX3OzcuVKBAUFwcHBAZGRkTh48GCN41esWIGwsDA4OjoiICAAc+fORVlZWT2lJQAovfg7/NO2Q5QEnOmxBK2au8gdiYiIyEjW5mbDhg2IiYlBbGwsjh49iq5du2LIkCHIysqqcvy6devw6quvIjY2FmfOnMGXX36JDRs24O9//3s9J2/CRBF5m+YBALbYDcSY4UNlDkRERGRK1uZm+fLlmDFjBqZMmYIOHTpg1apVcHJywurVq6sc//vvv+OBBx7AhAkTEBQUhMGDB+PJJ5+869oespz8w+vRsugUiiU1HIfGcidiIiJqcGRrbrRaLY4cOYLo6L8OH1YoFIiOjkZSUlKVj+nduzeOHDlibGYuXbqErVu3Yvjw4fWSucnTlUKMXwwA2OQ8HgN7dZY3DxERURVk26E4JycHBoMBPj6mJ33z8fHB2bNnq3zMhAkTkJOTgz59+kCSJOj1ejz77LM1bpbSaDTQaDTG2wUFBQAAnU4HnU5ngVfyl4r5LD1vQ5F1YCP8dZlIk1qg7ciXodfr6zyXrdfKklgr87FW5mOtaof1Mp+1alWb+QRJkiSLPruZrl+/Dn9/f/z++++IiooyLn/llVewZ88eHDhwoNJjEhMT8cQTT+DNN99EZGQkLly4gBdffBEzZszAwoULq3yexYsXY8mSJZWWr1u3Dk5OTpZ7QU3AF2cVcMo7h/auZejRkWttiIio/pSUlGDChAnIz8+Hm5tbjWNla260Wi2cnJzwww8/YPTo0cblkydPRl5eHn788cdKj+nbty/uv/9+vPfee8Zl33zzDZ555hkUFRVBoai8la2qNTcBAQHIycm5a3FqS6fTIT4+HoMGDYJKpbLo3HI7mpqH8Z8fhEIAtszujbbe93aElC3XytJYK/OxVuZjrWqH9TKftWpVUFAAT09Ps5ob2TZL2dvbo2fPnkhISDA2N6IoIiEhAbNnz67yMSUlJZUaGKWyfIfW6no0tVoNtVpdablKpbLaG9Sac8uiJBdf/XIEADCuZwDC/ZtZbGqbq5UVsVbmY63Mx1rVDutlPkvXqjZzyXoSv5iYGEyePBm9evVCREQEVqxYgeLiYkyZMgUAMGnSJPj7+2Pp0qUAgJEjR2L58uXo3r27cbPUwoULMXLkSGOTQ5aXseUt/PP612hu93/420Nvyh2HiIioRrI2N+PHj0d2djYWLVqEjIwMdOvWDdu3bzfuZJyammqypua1116DIAh47bXXkJaWBi8vL4wcORJvvfWWXC/B9hWko/mptbAXtGjTLhwBzbmfEhERNWyyX35h9uzZ1W6GSkxMNLltZ2eH2NhYxMbG1kMyAoDMrW/DB1ocFsMQ/fAEueMQERHdleyXX6AGrDATzc5+BwA41nYmAlo4yxyIiIjo7tjcULXSdyyHPXQ4KrbDsIfHyR2HiIjILGxuqGqlefA4tRYAcCJoGlo151obIiJqHNjcUJWun0yEUtTgrBiAvg9PlDsOERGR2WTfoZgapg+uBGOv5kM80laJf3hb9mSHRERE1sTmhirJyC/D5uQ06NAcwwb3ljsOERFRrXCzFJkSDfjfL7ugM0iICGqOHoGWOxsxERFRfeCaGzJRcvInPHNyMnxUveHSL07uOERERLXGNTdkIn/3hwCAIsdWGBDmLXMaIiKi2mNzQ0aGtGNomXcUOkkJ5z5/g0IhyB2JiIio1tjckFHmzhUAgJ1CFIbc313eMERERHXE5obKFWbC68oWAEBWhylwtOdV1omIqHFic0MAgNw9q6CCDkfEdoiOHi53HCIiojpjc0OAJEH3xyYAwGGf8Qho7iRzICIiorrjoeCEQo0eQ0teRx/9ATwxkJdaICKixo1rbgibj6XhplaJM56D0TuspdxxiIiI7gmbm6ZOV4b1B1MBABMiAiEIPPybiIgaNzY3TVzm1rfxyY3peMTuIB7t7i93HCIionvGfW6aMoMejie/hY8iB9393dDM2V7uRERERPeMa26aMM2ZbXDT5+CG5Ir2/Z+QOw4REZFFsLlpwm7s+xwAsFM1EJHt/GROQ0REZBlsbpqqoiz4ZO4DAIjd/4/XkSIiIpvB5qaJyk76FkqIOCa2RXTfvnLHISIishg2N02UeOw7AMApz2HwcXOQOQ0REZHl8GipJkg0iHhLNwF99QnwjpogdxwiIiKLYnPTBB28chP/K2yH3epwHOoWJnccIiIii+JmqSZo09E0AMDwzi3hoFLKnIaIiMiy2Nw0MZqLv6LTyaUIF67g0R48IzEREdkebpZqYrL3fIanhK1wdhIREfSc3HGIiIgsjmtumhJdGVpcjQcAlLQfy3PbEBGRTWJz04QUntoOR6kEaVILRPYdInccIiIiq2Bz04TcOLAeAHDAsS/a+brLnIaIiMg62Nw0FbpS+GbsBgBIHR6VOQwREZH1sLlpIgpPboGDVIZrkifu6z1I7jhERERWw+amifgj5TqyJXcccOyHQE9nueMQERFZDZubJuKTmxGI1KzEzV5z5I5CRERkVWxumoAbRRokXbwBEQoM7t5W7jhERERWxeamCfj94AFIkohO/m4IbOEkdxwiIiKr4hmKbZ1eg+h9j+OgWoVt7dbJnYaIiMjquObGxhWe3QVHqRQGKNGvVze54xAREVkdmxsbl3XwvwCAI+r70drTVeY0RERE1sfmxpaJIlqk7QIAaNsNkzkMERFR/WBzY8M0qYfgYbiBQskRYfezuSEioqaBzY0Nu76/fJPUQWUPhLfykjkNERFR/WBzY8OcUnYAAHIDBkEQBJnTEBER1Q8eCm6jRIOIBfoZiNAnoUvEI3LHISIiqjdsbmxUclo+dhUH45C6HY6EBcsdh4iIqN5ws5SNij+dCQDoF+YFezv+momIqOngt54t0hSi/ZEleEhxFIPCveVOQ0REVK+4WcoGZZ3YiVG6reiqOopm7V+VOw4REVG94pobG5R3fAsA4IxzBNwdVTKnISIiql9sbmyNJKFF+l4AgNhmkMxhiIiI6h+bGxujST+FFoZslEkqhNw3RO44RERE9Y7NjY25fugnAMBRRSe0D+DOxERE1PSwubE1F+IBAFk+fXlWYiIiapLY3NgS0QBlcfn5bdy78EKZRETUNPFQcBuSVqDFgyXvIljIxKZuveSOQ0REJAvZ19ysXLkSQUFBcHBwQGRkJA4ePFjj+Ly8PMyaNQstW7aEWq1GaGgotm7dWk9pG7Y957IBCGgeGA4PJ3u54xAREclC1jU3GzZsQExMDFatWoXIyEisWLECQ4YMwblz5+DtXXlnWK1Wi0GDBsHb2xs//PAD/P39ceXKFXh4eNR/+AZo77kMAEC/UC+ZkxAREclH1uZm+fLlmDFjBqZMmQIAWLVqFbZs2YLVq1fj1Vcrn1l39erVyM3Nxe+//w6VqvzkdEFBQfUZucHS5V3HuxdH4xFVR/i3XS93HCIiItnI1txotVocOXIECxYsMC5TKBSIjo5GUlJSlY/53//+h6ioKMyaNQs//vgjvLy8MGHCBMyfPx9KpbLKx2g0Gmg0GuPtgoICAIBOp4NOp7PgK4JxPkvPa44rh7agrVCMIGU22vi6ypKhNuSsVWPDWpmPtTIfa1U7rJf5rFWr2swnW3OTk5MDg8EAHx8fk+U+Pj44e/ZslY+5dOkSdu3ahYkTJ2Lr1q24cOECZs6cCZ1Oh9jY2Cofs3TpUixZsqTS8p07d8LJyeneX0gV4uPjrTJvTbxP/4i2AM7YdcSf27fV+/PXlRy1aqxYK/OxVuZjrWqH9TKfpWtVUlJi9thGdbSUKIrw9vbGZ599BqVSiZ49eyItLQ3vvfdetc3NggULEBMTY7xdUFCAgIAADB48GG5ubhbNp9PpEB8fj0GDBhk3m9ULSUL+8ZcAAK5dhmPAsOH199x1JFutGiHWynyslflYq9phvcxnrVpVbHkxh2zNjaenJ5RKJTIzM02WZ2ZmwtfXt8rHtGzZEiqVymQTVHh4ODIyMqDVamFvX/kIIbVaDbVaXWm5SqWy2hvUmnNXpSz9HDzFbGgkO7TrNbhR/Y9X37VqzFgr87FW5mOtaof1Mp+la1WbuWQ7FNze3h49e/ZEQkKCcZkoikhISEBUVFSVj3nggQdw4cIFiKJoXHb+/Hm0bNmyysamqbh2tHwz1B+K9ghq6SlzGiIiInnJep6bmJgYfP755/jqq69w5swZPPfccyguLjYePTVp0iSTHY6fe+455Obm4sUXX8T58+exZcsWvP3225g1a5ZcL6FBMFxMBABkekbykgtERNTkybrPzfjx45GdnY1FixYhIyMD3bp1w/bt2407GaempkKh+Kv/CggIwI4dOzB37lx06dIF/v7+ePHFFzF//ny5XkKD8FtZCArENDiERcsdhYiISHay71A8e/ZszJ49u8r7EhMTKy2LiorC/v37rZyq8cgv1eHNmwMhSgOx/76H5I5DREQkuzo3NzqdDhkZGSgpKYGXlxeaN29uyVxkpv2XbkCUgBAvZ/i6O8gdh4iISHa12uemsLAQn376Kfr16wc3NzcEBQUhPDwcXl5eaN26NWbMmIFDhw5ZKytV4cqJX+GGIjzQhjsSExERAbVobpYvX46goCCsWbMG0dHR2Lx5M5KTk3H+/HkkJSUhNjYWer0egwcPxtChQ/Hnn39aMzcBgCRh3PkYJKv/hqHN0+VOQ0RE1CCYvVnq0KFD2Lt3Lzp27Fjl/REREZg6dSpWrVqFNWvWYN++fWjXrp3FglJlN1NPoZmUjzKo0KHr/XLHISIiahDMbm6+++47s8ap1Wo8++yzdQ5E5ks7noBmAM7atUc3d1e54xARETUIFjnPTUFBATZv3owzZ85YYjoyk3j5NwBArmcvmZMQERE1HHVqbh5//HF88sknAIDS0lL06tULjz/+OLp06YL//ve/Fg1I1ZAktMw7AgBwaNtX5jBEREQNR52am71796Jv3/Iv1E2bNkGSJOTl5eGjjz7Cm2++adGAVLWizEvwEnOgk5Ro072/3HGIiIgajDo1N/n5+cbz2mzfvh1jx46Fk5MTRowYwaOk6sm15PJrcp1TtoWPZwuZ0xARETUcdWpuAgICkJSUhOLiYmzfvh2DBw8GANy8eRMODjyRXH3YrW2P+boZONbyCbmjEBERNSh1OkPxnDlzMHHiRLi4uKB169bo378/gPLNVZ07d7ZkPqrG7usqHDQMQM9uXeSOQkRE1KDUqbmZOXMmIiMjkZqaikGDBhkvbhkSEsJ9bupBmc6A5Kt5AID7gnnZCyIiotvV+dpSPXv2RM+ePU2WjRgx4p4D0d1dOP4bnsA2nHPphqAWTnLHISIialDM3ufmnXfeQWlpqVljDxw4gC1bttQ5FNWs7PhGvK76CnOcdkAQBLnjEBERNShmNzenT59GYGAgZs6ciW3btiE7O9t4n16vx4kTJ/Cvf/0LvXv3xvjx4+HqyjPmWotT1jEAgNQqQuYkREREDY/Zm6XWrl2L48eP45NPPsGECRNQUFAApVIJtVqNkpISAED37t0xffp0PP300zxqykpEvQ7BmvIzQXuF8+R9REREd6rVPjddu3bF559/jn//+984ceIErly5gtLSUnh6eqJbt27w9PS0Vk665dq5wwiEBoWSI4LDe8gdh4iIqMGp0w7FCoUC3bp1Q7du3Swch+4m+/SvCARwSR2OrnZ13h+ciIjIZlnkwplUf4S0gwCAQq/uMichIiJqmNjcNDJeBacAAI4h98uchIiIqGHido1GpKBMh2Glr6OzcAmfdB8odxwiIqIGiWtuGpHjV/NQJDkizeM+tGjOi2USERFV5Z6amwsXLmDHjh3Gk/tJkmSRUFS1o1fyAADdAz1kzUFERNSQ1am5uXHjBqKjoxEaGorhw4cjPT0dADBt2jS89NJLFg1If2l//G28Zvc1+nkWyR2FiIiowapTczN37lzY2dkhNTUVTk5/Xdto/Pjx2L59u8XC0V9EgwG9C7dhut02dPbirlJERETVqdO35M6dO7Fjxw60atXKZHm7du1w5coViwQjU1cvnERrlKJMUiGoQ8+7P4CIiKiJqtOam+LiYpM1NhVyc3OhVqvvORRVln4mCQBwxb4tVCp7mdMQERE1XHVqbvr27Yu1a9cabwuCAFEUsWzZMgwYMMBi4egvhmtHAAAFzTvLnISIiKhhq9NmqWXLlmHgwIE4fPgwtFotXnnlFZw6dQq5ubn47bffLJ2RAHjklZ+8zz6Am6SIiIhqUqc1N506dcL58+fRp08fjBo1CsXFxRgzZgyOHTuGNm3aWDpjk1em0SBEdwEA4BPOMxMTERHVpM6H3bi7u+Mf//iHJbNQNS5e/BPecIQIBXyCuVmKiIioJnVubsrKynDixAlkZWVBFEWT+x555JF7DkZ/OZrvgoWaf+Hhtmp8olDKHYeIiKhBq1Nzs337dkyaNAk5OTmV7hMEAQaD4Z6D0V+OX8sHICAkMFDuKERERA1enfa5ef755zFu3Dikp6dDFEWTHzY2lnfyWj4AoEsrD3mDEBERNQJ1WnOTmZmJmJgY+Pj4WDoP3aGktARf5E3FWVUAunh9L3ccIiKiBq9Oa24ee+wxJCYmWjgKVSXl1CEECNmIUJ6Ht6en3HGIiIgavDqtufnkk08wbtw47Nu3D507d4ZKpTK5/4UXXrBIOAJuXjgIALjmGAZ3QZA5DRERUcNXp+bmu+++w86dO+Hg4IDExEQIt33pCoLA5saChIzjAIDSFjwEnIiIyBx1am7+8Y9/YMmSJXj11VehUNRpyxaZqXnBWQCAU+vuMichIiJqHOrUmWi1WowfP56NjZUVlJQi2HAZAODXPlLeMERERI1EnbqTyZMnY8OGDZbOQne4eOY4HAQdSuAAD/9QueMQERE1CnXaLGUwGLBs2TLs2LEDXbp0qbRD8fLlyy0SrqlLSc+GQQyFs4srwnlmYiIiIrPUqbk5efIkuncv3wfkjz/+MLlP4BE9FrO3qBU2axfj5fvCEC53GCIiokaiTs3N7t27LZ2DqnA6vQAA0KGlm8xJiIiIGg/uEdxAlWn1SMvOBQB08GNzQ0REZC6z19yMGTMGcXFxcHNzw5gxY2ocu3HjxnsO1tRdunwRJ1RTkCK0grfzMbnjEBERNRpmNzfu7u7G/Wnc3d2tFojKZZ0/hA6CBAc7BQSl6u4PICIiIgC1aG7WrFmD119/HfPmzcOaNWusmYkA6NLKz0yc7x6GVjJnISIiakxqtc/NkiVLUFRUZK0sdBvn3DPl//DlZReIiIhqo1bNjSRJ1spBtxFFCX5lFwAAHiE9ZU5DRETUuNT6aCmex8b6UjOyECSkAwB8QyNkTkNERNS41Po8N6GhoXdtcHJzc+sciIDr5w4jCECOogU8Xb3kjkNERNSo1Lq5WbJkCY+WsrI/bxqQbugL3xY+8JQ7DBERUSNT6+bmiSeegLe3tzWy0C2J+b7YrXsOb9zXCQ/IHYaIiKiRqdU+N9zfpn6cus7LLhAREdUVj5ZqYHIKy+BadAl2ggHhLV3ljkNERNTo1Kq5EUXRKpukVq5ciaCgIDg4OCAyMhIHDx4063Hr16+HIAgYPXq0xTPJ5WJKChLUL+MP9TQ4KUS54xARETU6sl84c8OGDYiJiUFsbCyOHj2Krl27YsiQIcjKyqrxcZcvX8a8efPQt2/fekpaP3JTyq8jlafyBuzsZU5DRETU+Mje3CxfvhwzZszAlClT0KFDB6xatQpOTk5YvXp1tY8xGAyYOHEilixZgpCQkHpMa3369FMAgEK3djInISIiapxqfbSUJWm1Whw5cgQLFiwwLlMoFIiOjkZSUlK1j3v99dfh7e2NadOmYd++fTU+h0ajgUajMd4uKCjfWVen00Gn093jKzBVMd+9zOtw8xwAQPQMs3i+hsQStWoqWCvzsVbmY61qh/Uyn7VqVZv5ZG1ucnJyYDAY4OPjY7Lcx8cHZ8+erfIxv/76K7788kskJyeb9RxLly7FkiVLKi3fuXMnnJycap3ZHPHx8XV6nCgBIaWXAAWQWmiHs1u3WjhZw1PXWjVFrJX5WCvzsVa1w3qZz9K1KikpMXusrM1NbRUWFuKpp57C559/Dk9P805vt2DBAsTExBhvFxQUICAgAIMHD4abm2UPtdbpdIiPj8egQYOgUqlq/fjUG0XwPXYNANB3xJNQeodZNF9Dcq+1akpYK/OxVuZjrWqH9TKftWpVseXFHLI2N56enlAqlcjMzDRZnpmZCV9f30rjL168iMuXL2PkyJHGZaJYfkSRnZ0dzp07hzZt2pg8Rq1WQ61WV5pLpVJZ7Q1a17nTUy+gjaCBFio4+LYHlI2q96wTa/4ebA1rZT7WynysVe2wXuazdK1qM5esOxTb29ujZ8+eSEhIMC4TRREJCQmIioqqNL59+/Y4efIkkpOTjT+PPPIIBgwYgOTkZAQEBNRnfIs7f0OP93WP4dfmY5tEY0NERGQNsn+DxsTEYPLkyejVqxciIiKwYsUKFBcXY8qUKQCASZMmwd/fH0uXLoWDgwM6depk8ngPDw8AqLS8MTqW54CfDGPwatf2eEjuMERERI2U7M3N+PHjkZ2djUWLFiEjIwPdunXD9u3bjTsZp6amQqGQ/Yj1enE+oxAAEObDMxMTERHVlezNDQDMnj0bs2fPrvK+xMTEGh8bFxdn+UAy0OpFeOXsR7HghVAfZ7njEBERNVoNorkhICUzD6vt3oG9YIAkDATABoeIiKgumsb2nkbg2qU/YC8YUCo4QnBv3DtGExERyYnNTQNReLX8sgs3HFoDgiBzGiIiosaLzU0DIWWfBwBoPNrKnISIiKhxY3PTQDgVXAQA2Pm0lzkJERFR48bmpgEo1RrQUpcKAGjeuqPMaYiIiBo3NjcNwKXsArQRrgMAXFs1/pMREhERyYmHgjcAKVmF+Ew3DX2b5eKx5sFyxyEiImrU2Nw0ABdulOFHsQ/Uwa3wmJIXZCMiIroX3CzVAFzMLgYAtPFykTkJERFR48fmpgFwTvsdfRQnEeamlzsKERFRo8fNUjITRQljCr9BhP1pZBe3BBAmdyQiIqJGjWtuZJZeUIZgXAMANGvNI6WIiIjuFZsbmV25eg1eQgEAwM6ba22IiIjuFZsbmd1M/QMAkKv0AtTcoZiIiOhesbmRmTbjLAAg34XntyEiIrIENjcyU928AADQNw+VOQkREZFtYHMjM4/iFACAgy/3tyEiIrIEHgouoyKNHkvLxiBc0QuxnYfKHYeIiMgmcM2NjC5lF+GUFIxEx8Fw9eNmKSIiIktgcyOji9lFAIA2Xs4yJyEiIrIdbG5klH/lBCYqf0E/l1S5oxAREdkM7nMjI5dre/GWajVS8lMBjJc7DhERkU3gmhsZqQsuAwAUnm3lDUJERGRD2NzIxCBKaFF2FQDg4tde5jRERES2g82NTNJuliJQyAAAeLRic0NERGQpbG5kkpKeAz/cAAAouVmKiIjIYtjcyCTn6lkoBAklCmfA2VPuOERERDaDzY1MSjLOAwAKHAMBQZA5DRERke1gcyOTX8ra43HNQlzs9orcUYiIiGwKz3Mjk1M3JORI4XAL7yN3FCIiIpvCNTcyyC/RIadICwAI4aUXiIiILIprbmRwMacILyr/izJHbzjjQQCuckciIiKyGWxuZHDleibmqv4L6AGI8+WOQ0REZFO4WUoGeWnnAADFdh6AYzN5wxAREdkYNjcy0GddAAAUObeWOQkREZHtYXMjA/v8FACA2CxE5iRERES2h81NPZMkCa6l5RfMVHu3kTkNERGR7WFzU89yirTwkzIBAK5+oTKnISIisj1sburZlRvFCBTKmxuVJ9fcEBERWRqbm3p2+UYJxmiW4A2v9wDvcLnjEBER2Rye56aeXblRjAy0QKlfIGDPsxMTERFZGtfc1LMrN0oAAEEtnGROQkREZJvY3NSz5ul78IrdenTXH5c7ChERkU1ic1PP2hQcxEy7/yEkP0nuKERERDaJzU09yivRwteQAQBw9W0ncxoiIiLbxOamHl25UYIAIQsAYO/FsxMTERFZA5ubenQ5pwiBt5obNAuWNwwREZGNYnNTj7IzrsJJ0ECEAnAPkDsOERGRTWJzU49KMy8CAIrUPoCdvcxpiIiIbBObm3ok5ZZfDVzj1lrmJERERLaLzU09+qY4Ag+UfYjcfkvljkJERGSzePmFelKk0SOrWA/AC75tOssdh4iIyGZxzU09Sb112YVmTiq4O6pkTkNERGS7uOamnqTmFuNtuy+gcvACSnoBTs3ljkRERGST2NzUk+vZuZhqtwsoAYB35I5DRERksxrEZqmVK1ciKCgIDg4OiIyMxMGDB6sd+/nnn6Nv375o1qwZmjVrhujo6BrHNxTFtw4DL1O6cK0NERGRFcne3GzYsAExMTGIjY3F0aNH0bVrVwwZMgRZWVlVjk9MTMSTTz6J3bt3IykpCQEBARg8eDDS0tLqOXnt6G9cAQCUOLWSOQkREZFtk725Wb58OWbMmIEpU6agQ4cOWLVqFZycnLB69eoqx3/77beYOXMmunXrhvbt2+OLL76AKIpISEio5+S1oyy8CgAQeWZiIiIiq5K1udFqtThy5Aiio6ONyxQKBaKjo5GUlGTWHCUlJdDpdGjevOFu6pEkCU4l1wEA9i14Aj8iIiJrknWH4pycHBgMBvj4+Jgs9/HxwdmzZ82aY/78+fDz8zNpkG6n0Wig0WiMtwsKCgAAOp0OOp2ujsmrVjHfnfNmF2rgK5VvZlO3CLT48zZG1dWKKmOtzMdamY+1qh3Wy3zWqlVt5mvUR0u98847WL9+PRITE+Hg4FDlmKVLl2LJkiWVlu/cuRNOTk5WyRUfH29yO6UQeFC4AQA4npKD9JtbrfK8jdGdtaLqsVbmY63Mx1rVDutlPkvXqqSkxOyxsjY3np6eUCqVyMzMNFmemZkJX1/fGh/7z3/+E++88w5++eUXdOnSpdpxCxYsQExMjPF2QUGBcSdkNze3e3sBd9DpdIiPj8egQYOgUv11or7/HU/HuD9iMTjAgI/G9kN3tatFn7cxqq5WVBlrZT7WynysVe2wXuazVq0qtryYQ9bmxt7eHj179kRCQgJGjx4NAMadg2fPnl3t45YtW4a33noLO3bsQK9evWp8DrVaDbVaXWm5SqWy2hv0zrnTCzQwQAknr9ZQuTTcfYPkYM3fg61hrczHWpmPtaod1st8lq5VbeaSfbNUTEwMJk+ejF69eiEiIgIrVqxAcXExpkyZAgCYNGkS/P39sXRp+cUm3333XSxatAjr1q1DUFAQMjIyAAAuLi5wcXGR7XXU5GpuKQAgoLmjzEmIiIhsn+zNzfjx45GdnY1FixYhIyMD3bp1w/bt2407GaempkKh+Ougrk8//RRarRaPPfaYyTyxsbFYvHhxfUY3m33mUaxQbUBQXn8A8+WOQ0REZNNkb24AYPbs2dVuhkpMTDS5ffnyZesHsjC3vDMYrfwdN/Oq3umZiIiILEf2k/jZOr1BhHNZOgBA1SJI3jBERERNAJsbK0vPL4M/sgEATl7BMqchIiKyfWxurOzqzRL4CzkAAEWzQJnTEBER2T42N1Z27WYpWgnla27gwetKERERWRubGytLz8mDN/LKb3jwulJERETWxubGyvKzr0ECoFOoAacWcschIiKyeWxurOxEkTvCNF8hcfAOQBDkjkNERGTz2NxY2dWbJdDDDl7+PFKKiIioPrC5saIynQGZBRoAQEAzXnqBiIioPjSIMxTbqvT8MsxSbkaY8jqa57gDLn3kjkRERGTz2NxYUdrNUjyoPIFIxVmgMEPuOERERE0CN0tZ0fW8289xwxP4ERER1Qc2N1aUdrMIPrhZfsO9lbxhiIiImgg2N1ZUlHMNdoIIg6AEXHzkjkNERNQksLmxIn3uVQCAxsEbUChlTkNERNQ0sLmxIqEwDQBgcPGTOQkREVHTwebGSkRRglhyEwZJgKIZL5hJRERUX9jcWElOkQZrdQPRXrsW9qM/lDsOERFRk8HmxkrS8koBAJ5uzlA5ecgbhoiIqAlhc2Ml1/PKAAD+HrzsAhERUX3iGYqtJC2vBP9WLUeLEg+gIBhwayl3JCIioiaBzY2VZOYWYrriCBSFEqBgmYmIiOoLN0tZSVHONSgECQZBBTh7yh2HiIioyWBzYyViXvkJ/LROvoAgyJyGiIio6eD2EitRFl0HAEhu/jInIWo4DAYDdDqd1ebX6XSws7NDWVkZDAaD1Z7HFrBWtcN6me9eamVvbw+F4t7Xu7C5sYIijR4euixABaia8wR+RJIkISMjA3l5eVZ/Hl9fX1y9ehUC15jWiLWqHdbLfPdSK4VCgeDgYNjb299TBjY3VpCeX4aWwg0AgIpnJyYyNjbe3t5wcnKy2peDKIooKiqCi4uLRf76s2WsVe2wXuara61EUcT169eRnp6OwMDAe/qcYHNjBdfzSuEILQxQQOnOzVLUtBkMBmNj06JFC6s+lyiK0Gq1cHBw4BfQXbBWtcN6me9eauXl5YXr169Dr9dDpVLVOQN/Q1ZwPb8Mr+j/hueCtgHdn5I7DpGsKvaxcXJykjkJETV0FZuj7nW/JjY3VlBxdmLfZi6AnVrmNEQNA/dTIKK7sdTnBJsbK0jPL29u/HjpBSK6gyAI2Lx5c41jnn76aYwePbpe8tRV//79MWfOHLljEFWJzY0VGHKv4Hv7JRh26S25oxDRPXj66achCAKeffbZSvfNmjULgiDg6aefrvP8ly9fhiAISE5ONln+4YcfIi4urs7z1oeNGzfijTfekDtGrcXFxcHDw0PuGGRlbG6swK7wKiIU5+B986jcUYjoHgUEBGD9+vUoLS01LisrK8O6desQGBholed0d3dv8F/AzZs3h6urq9wxiKrE5sbCJAlQl6SX3+AJ/IgavR49eiAgIAAbN240Ltu4cSMCAwPRvXt3k7FBQUFYsWKFybJu3bph8eLFVc4dHBwMAOjevTsEQUD//v0BmLdZ6l//+hfatWsHBwcH+Pj44LHHHjPe179/f8yePRuzZ8+Gu7s7PD09sXDhQkiSZByj0WiwcOFCBAQEwNnZGZGRkUhMTDR5jt9++w39+/eHk5MTmjVrhiFDhuDmzZvG57h9s5RGo8G8efPg7+9f5XxXrlzByJEj0axZMzg7O6Njx47YunVrrV/f2rVr0aJFC2g0GpPxo0ePxlNPlR/Acfz4cQwYMACurq5wc3NDz549cfjwYSQmJmLKlCnIz8+HIAgQBMH4u7lb/ri4OLRu3Ro///wzwsLC4OTkhMceewwlJSX46quvEBQUhGbNmuGFF17gSf4aAB4KbmGlBsDTkAMoeAI/oupIkoRSneW/AERRRKnWADutvspDUB1VyjrtsDh16lSsWbMGEydOBACsXr0aU6ZMqdQM1NbBgwcRERGBX375BR07djT7xGWHDx/GCy+8gK+//hq9e/dGbm4u9u3bZzLmq6++wrRp03Dw4EEcPnwYzzzzDAIDAzFjxgwAwPPPP4+TJ09i3bp1aNWqFTZt2oShQ4fi5MmTaNeuHZKTkzFw4EBMnToVH374Iezs7LB79+5qv7hnz56N06dPY/369fDz86s036xZs6DVarF37144Ozvj9OnTcHFxqfXrGzduHF544QX873//w7hx4wAAWVlZ2LJlC3bu3AkAmDhxIrp3745PP/0USqUSycnJUKlU6N27N1asWIFFixbh3LlzAGDMcLf8AFBaWoqPP/4Y69evR2FhIcaMGYNHH30UHh4e2Lp1Ky5duoSxY8figQcewPjx4836XZJ1sLmxsDwN4HfrBH52HmxuiKpSqjOgw6Id9f68p18fAif72n/s/d///R8WLFiAK1euAChfo7F+/fp7bm68vLwAAC1atICvr6/Zj0tNTYWzszMefvhhuLq6onXr1pXWIgUEBOCDDz6AIAgICwvDyZMn8cEHH2DGjBlITU1FXFwcTp48ibCwMCgUCsybNw/bt2/HmjVr8Pbbb2PZsmXo1asX/vWvfxnn7NixY7V51qxZg9TUVPj5+QFApflSU1MxduxYdO7cGQAQEhJSp9fn6OiICRMmYM2aNcbm5ptvvkFgYKBxzVdqaipefvlltG/fHgCMzQlQvslPEASTepuTHyg/rUHFGiUAeOyxx/D1118jMzMTLi4u6NChAwYMGIDdu3ezuZEZmxsLy9cKaCfklt9waylvGCKyCC8vL4wYMQJxcXGQJAkjRoyAp6dnvTz3t99+i7/97W/G29u2bcOgQYPQunVrhISEYOjQoRg6dCgeffRRk3MJ3X///SZrqaKiovD+++/DYDDg5MmTMBgMuO+++0yeS6PRGE+0mJycbGwe7qZivtDQ0Grne+GFF/Dcc89h586diI6OxtixY9GlS5cq57vb65sxYwbuu+8+pKWlwd/fH3FxccadvwEgJiYG06dPx9dff43o6GiMGzcObdq0uaf8QPm5mm6fx8fHB0FBQSZroHx8fJCVlWVO2ciK2NxYWJ4W8BHKt0nD1U/eMEQNlKNKidOvD7H4vKIoorCgEK5urtVulqqrqVOnYvbs2QCAlStXVjlGoVCY7NcC4J4vFPrII48gMjLSeNvf3x+Ojo44evQoEhMTsXPnTixatAiLFy/GoUOHzNoRuaioCEqlErt374a7u7tJrSq+qB0dzT+VRcV8R44cgVJpWuOK+aZPn44hQ4YYNx8tXboU77//Pp5//vlK87m6utb4+rp3746uXbti7dq1GDx4ME6dOoUtW7YYH7948WJMmDABW7ZswbZt2xAbG4v169fj0UcfrXN+ALCzM/3KFASh0ll0BUGAKIpmVI2sic2NheVpAQGACAUUruavZiZqSgRBqNPmobsRRRF6eyWc7O0sfor8oUOHQqvVQhAEDBlSdWPm5eWF9PR04+2CggKkpKRUO6c5Z2N1dXWt8qgkOzs7REdHIzo6GrGxsfDw8MCuXbswZswYAMCBAwdMxu/fvx/t2rWDUqlE9+7dYTAYkJ2djZ49e1ZZqy5duiAhIQFLliypNluFivmysrLQt2/fascFBATg2WefxbPPPosFCxbg888/r7K5Mef1TZ8+HStWrEBaWhqio6MREGC6G0BoaChCQ0Mxd+5cPPnkk1izZg0effRR2NvbV6q3ufmp8eDRUhaWrxXwsPZtfPJAEuBb9SpXImp8lEolzpw5g9OnT1f6677CQw89hK+//hr79u3DyZMnMXny5GrHAoC3tzccHR2xfft2ZGZmIj8/36wsP//8Mz766CMkJyfjypUrWLt2LURRRFhYmHFMamoqYmJicO7cOXz33Xf4+OOP8eKLLwIo/+KfMGECnnvuOWzcuBEpKSk4ePAgli5dalwDsmDBAhw6dAgzZ87EiRMncPbsWXz66afIycmplCc0NBQTJ07EpEmTqp1vzpw52LFjB1JSUnD06FHs3r0b4eHhdX59EyZMwLVr1/D5559j6tSpxuWlpaWYPXs2EhMTceXKFfz22284dOiQ8bmCgoJQVFSEhIQE5OTkoKSkxKz81LiwubGwPG35f309nAFeXI3Ipri5ucHNza3a+xcsWIB+/frh4YcfxogRIzB69Oga9/Wws7PDRx99hH//+9/w8/PDqFGjzMrh4eGBjRs34qGHHkJ4eDhWrVqF7777zmSH30mTJqG0tBQRERGYNWsWXnzxRTzzzDPG+1evXo0nnngCL7/8MsLCwjB69GgcOnTIeO6e0NBQ7Ny5E8ePH0dERASioqLw448/Vto0U2HNmjWYNGkSXnrppSrnMxgMmDVrFsLDwzF06FCEhoaa7Kxc29fn7u6OsWPHwsXFxeSweaVSiRs3bmDSpEkIDQ3F448/jmHDhhnXQPXu3RvPPvssxo8fDy8vLyxbtsys/NS4CNKdG4htXEFBAdzd3ZGfn1/jh1Rd6HQ6PLh0B9JLBHw1NQL9Qr0sOr8t0el02Lp1K4YPH35PV35tChp7rcrKypCSkoLg4GA4ODhY9blEUURBQQHc3Nya9JWb+/fvj27dulU6587tbKFWAwcORMeOHfHRRx9Z/blsoV715V5qVdPnRW2+v/kbsrAOupPYYP86Op77WO4oREQ26ebNm9i0aRMSExMxa9YsueNQA8Qdii1IqxfhL6YjUnUW2sLqV0UTEVHdde/eHTdv3sS7775rsh8OUQU2NxZ0s0QL31uHgas8eOkFIpLHvZ5csKG7fPmy3BGogeNmKQvKKdIaz3EjuPIEfkRERHJgc2NBucVa+KDi7MQ8gR8REZEc2NxY0I1iLXyEvPIbPIEfERGRLNjcWFB5c8NLLxAREcmJzY0F5RUUoRgOEKHkRTOJiIhkwubGgrJKgSjNJ/i0z2+AuvK1YIiIiMj62NxY0M2S8msveDhb9yysRCS//v37Y86cOfX2fHFxcTVe8fvy5csQBAHJycnVjhEEAZs3b7Z4tjvdLWtDsnjxYnTr1s3s8ebUmeTH5saCijTlV5p1deDpg4hswdNPPw1BECr9XLhwARs3bsQbb7xhHBsUFFTpcgcN7Us+PT0dw4YNs+icVb3u8ePH4/z58xZ9nsYsLi7O+N5RKBRo1aoVpkyZgqysrDrP15DeV4sXLza+Pjs7O4SEhODvf/87ioqKAMjTEPJb2IJ652/FPPt4eKSOA7rPkzsOEVnA0KFDsWbNGpNlXl5eNV7tu6Hy9a2fozgdHR3h6OhYL8/VWLi5ueHcuXMQRRHHjx/HlClTcP36dezYsaPS2MuXLyM4OBjWuvTjzZs3oVKp4OLiUu2Y1NTUWl00tGPHjvjll1+g1+uxb98+TJ8+HXq9Hp999pklItca19xYkL82BZGKs3DVZsodhYgsRK1Ww9fX1+RHqVSabJbq378/rly5grlz5xr/gk1MTMSUKVOQn59vXLZ48WIAgEajwbx58+Dv7w9nZ2dERkZWOqtwXFwcAgMD4eTkhEcffRQ3btyoVW6DwYCpU6eiffv2SE1NBWC6Wery5cto1qwZNm7ciAEDBsDJyQldu3ZFUlKSyTy//vor+vbtC0dHRwQEBOCFF15AcXFxta+7IvudaxZ++ukn3HfffXBwcICnpyceffTRarNXbCpavXo1AgMD4eLigpkzZ8JgMGDZsmXw9fWFt7c33nrrLZPHpaamYtSoUXBxcYGbmxsef/xxZGaafh6/88478PHxgaurK6ZNm4aysrJKz//FF18gPDwcDg4OaN++fbVXL68NQRDg6+sLPz8/DBs2DC+88AJ++eUXlJaW3vPc5tDr9diyZQvGjRuHli1b4uLFizWODw4ORnR0NL7++muUlJTcdX47Ozv4+vqiVatWGD9+PMaNG4effvrJUvFrjc2NBXkYyj98FDw7MZF5tMXV/+jKajG29O5jrWjjxo1o1aoVXn/9daSnpyM9PR29e/fGihUr4ObmZlw2b175Gt3Zs2cjKSkJ69evx4kTJzBu3DgMHToUf/75JwDgwIEDmDZtGmbPno3k5GQMGDAAb775ptl5NBoNxo0bh+TkZOzbt6/Gv8AXLlyIefPmITk5GaGhoXjyySeh1+sBABcvXsTQoUMxduxYnDhxAhs2bMCvv/6K2bNnV/u6q7JlyxY8+uijGD58OI4dO4aEhARERETU+BouXryIbdu2Yfv27fjuu+/w5ZdfYsSIEbh27Rr27NmDd999F6+99hoOHDgAoPxK1KNGjUJubi727NmD+Ph4XLp0CePHjzfO+f3332Px4sV4++23cfjwYbRs2bJS4/Ltt99i0aJFeOutt3DmzBm8/fbbWLhwIb766qu7F74WHB0dIYqisdbWcvLkSbz00kto1aoVJk2aBC8vL+zevRtdu3at8XGnT59GREQEXnvtNfj4+GDq1KnYs2eP2WuTHBwcoNVqLfES6kZqAD755BOpdevWklqtliIiIqQDBw7UOP7777+XwsLCJLVaLXXq1EnasmWL2c+Vn58vAZDy8/PvNbYJURSlQwvvk6RYNykraZ1F57ZFWq1W2rx5s6TVauWO0uA19lqVlpZKp0+flkpLSyvfGetW/c83j5mOfdO3+rGrh0uSJEkGg0G6efOmJL4bXHlMHUyePFlSKpWSs7Oz8eexx8pz9evXT3rxxReNY1u3bi198MEHJo9fs2aN5O7ubrLsypUrklKplNLS0kyWDxw4UFqwYIEkSZL05JNPSsOHDze5f/z48ZXmul1KSooEQNq3b580cOBAqU+fPlJeXp7JGADSpk2bJEmSpIsXL0oApM8++8x4/6lTpyQA0pkzZyRJkqRp06ZJzzzzjMkc+/btkxQKhfH3ac7rjoqKkiZOnFht9jvFxsZKTk5OUkFBgXHZkCFDpKCgIMlgMBiXhYWFSUuXLpUkSZJ27twpKZVKKTU1tdLrOXjwoDHHzJkzTZ4rMjJS6tq1q/F2mzZtpHXrTD/D33jjDSkqKkq6efOmsW7Hjh0z+/XcWY/z589LoaGhUq9evaocX/G7NHe+O+Xk5EgrVqyQunfvLtnb20ujR4+W/vvf/0oajcbszBVEUZR27dolPf3005Krq6sUHBwsxcbGSpcuXTKOiY2NNanhwYMHpRYtWkhjx441eT3m1Kymz4vafH/LvuZmw4YNiImJQWxsLI4ePYquXbtiyJAh1e5o9fvvv+PJJ5/EtGnTcOzYMYwePRqjR4/GH3/8Uc/JTWn0ovHSC+pmrWTNQkSWM2DAACQnJxt/Pvroo3ua7+TJkzAYDAgNDYWLi4vxZ8+ePcZNBWfOnEFkZKTJ46Kiosya/8knn0RxcTF27twJd3f3u47v0qWL8d8tW5avda74/D1+/Dji4uJMcg4ZMgSiKCIlJcWsPACQnJyMgQMHmj0eKN9R2dX1r1Nq+Pj4oEOHDlAoFCbLKrKeOXMGAQEBCAgIMN7foUMHeHh44MyZM8YxNdW1uLgYFy9exLRp00xe85tvvnnXzTh3k5+fDxcXFzg5OSEsLAw+Pj749ttvjfd37NjR+HwdO3YEAJMMtdkR/OOPP8acOXPg4uKCCxcuYNOmTRgzZgzs7e0rjR02bFil572dIAgYMGAA1qxZg2vXriEqKgpLlizB3LlzTcadPHkSLi4ucHR0xP3334/77rsPH3/8sdmZLU32HYqXL1+OGTNmYMqUKQCAVatWYcuWLVi9ejVeffXVSuM//PBDDB06FC+//DIA4I033kB8fDw++eQTrFq1ql6z366oTAfvW2cnVjfj2YmJzPL369XfJ9yxw+7LF2oYa/p3mvTCcQgKy/zt5uzsjLZt21pkLgAoKiqCUqnEkSNHKu2UXNMOnuYaPnw4vvnmGyQlJeGhhx6663iVSmX8d8U+M6IoGrP+7W9/wwsvvFDpcbXZ2bQuOxffnqsiW1XLKrJaQsXRPZ9//nmlJqiiNnXl6uqKo0ePQqFQoGXLlpVqsnXrVuh0OgBAWloa+vfvb3J0UW1q+Mwzz8DOzg5r165Fx44dMXbsWDz11FPo37+/SXMIlO9fVLHfz531rXD06FGsXbsW3333HQRBQExMDKZPn24yJiwsDP/73/+M+96UlZXBzc3N7MyWJmtzo9VqceTIESxYsMC4TKFQIDo6utJObRWSkpIQExNjsmzIkCH1cu6GmpTkZcFTKN92qnDjdaWIzGLvbL2xFmpuzH5Ke3sYDIa7LuvevTsMBgOysrLQt2/fKucKDw837ktSYf/+/WbleO6559CpUyc88sgj2LJlC/r161eLV2GqR48eOH36dI3NXVWv8U5dunRBQkKC8Y9YawgPD8fVq1dx9epV49qb06dPIy8vDx06dDCOOXDgACZNmmR83O119fHxgZ+fHy5duoSJEyeazC+KIgoKCuqcT6FQ1FjH1q1bG/9tZ1f+1VzXptrPzw+vvfYaXnvtNfz+++/46quvMGbMGLi6umLixIl46qmnjGtp/P39q5zj2rVr+Oabb/D111/j4sWLGDlyJL788ksMHTrUmO929vb2xryiKFa5o3Z9krW5ycnJgcFggI+Pj8lyHx8fnD17tsrHZGRkVDk+IyOjyvEajQYajcZ4u+LNqdPpjF2yJRTdzEK61BxKiHARBcCCc9uiitpb8ndgqxp7rXQ6HSRJgiiKFv0ruyrSrZ0dK57PEvPVNNft97Vu3Rp79uzB448/DrVaDU9PTwQGBqKoqAjx8fHo2rUrnJyc0LZtW0yYMAGTJk3Ce++9h+7duyM7Oxu7du1C586dMWLECMyePRt9+/bFe++9h0ceeQQ7d+7E9u3bAaDaLBXLRVHErFmzoNfr8fDDD2PLli3o06ePyThRFKus1e3/FUURL7/8Mnr37o1Zs2Zh2rRpcHZ2xunTp/HLL78YNzlU9brvnG/hwoUYNGgQQkJCMH78eOj1emzbtg2vvPJKtXW987VW97uoWPbQQw+hc+fOmDhxIpYvXw69Xo/Zs2ejX79+6NGjB0RRxPPPP4+pU6eiR48eeOCBB7Bu3TqcOnUKISEhxnljY2MxZ84cuLm5YciQIdBoNDh8+DBu3ryJ6dOnm2Qz9z12Zz3udbwoijAYDDh69KjJcrVajfDwcJNl999/P+6//3588MEH2Lx5M7766iv885//xJEjR9C5c+dqM7Ru3Rq9evXCzJkz8cQTT6BZs2aV8lW48/d153urYvmZM2cqPbZjx44ma4wq3ps6na7Sms3afAbKvlnK2pYuXYolS5ZUWr5z5044OTlZ7HkuFQCr9B+juUrEq/HxFpvX1sWzVmZrrLWqWE1dVFRUb0dPFBYWWmQenU4HvV5f5V/ser0eWq3WeN8rr7yCuXPnol27dtBoNLh58yY6deqEKVOm4IknnkBubi7mz5+PV199FStWrMA///lPvPTSS0hPT0eLFi3Qq1cv9OvXDwUFBejQoQM+/PBDLF26FLGxsejXrx9eeuklvPfee9WuPajYpFJcXIyCggJMmTIFJSUlePjhh/Gf//zHuJmltLQUBQUFxsO5S0pKjHNW1K1iWVBQEH7++We8+eab6NevHyRJQlBQEB599NEaX3dZWRkkSTKO6dGjB+Li4vDee+/h3XffhaurK3r37l3ta9FoNDAYDCb3V/W7uPN3sHbtWsyfP9+4+WXgwIF49913jfcPGzYM8+bNw/z586HRaDBy5EhMmTIFu3btMo55/PHHIQgCPv74Y7zyyitwcnJChw4d8Nxzzxnre3udgfI1UxMmTKhyVwoAlepxNxW/y+rGl5WVoaioCD179jRZHhwcXKnhud3w4cMxfPhwpKenw9nZucY8SUlJCA0NNd6uaWxVvy/gr/dTxeuZMGFCpcf+8ccfJmuPtFotSktLsXfv3kpHkplzSHoFQZKsdJYgM2i1Wjg5OeGHH37A6NGjjcsnT56MvLw8/Pjjj5UeExgYiJiYGJPTnsfGxmLz5s04fvx4pfFVrbkJCAhATk6OxbcH6nQ67NwZj8GDB1W77ZLK6XQ6xMfHY9Ag1upuGnutysrKcPXqVQQFBcHBwbqXJpEkCYWFhXB1db3nfSRsHWtVO9XVq6SkBF5eXtiyZQv69+8vX8AG5F7eW2VlZbh8+TICAgIqfV4UFBTA09MT+fn5d/3+lnXNjb29PXr27ImEhARjcyOKIhISEoznUbhTVFQUEhISTJqb+Pj4ao8kUKvVUKvVlZarVCqrfFEIgvXmtkWslfkaa60MBoPxtPN37sxoaRWrvCuej6rHWtVOdfXas2cPHnroIbN23m4q7uW9pVAojDuP3/l5V5vPP9k3S8XExGDy5Mno1asXIiIisGLFChQXFxt3PJs0aRL8/f2xdOlSAMCLL76Ifv364f3338eIESOwfv16HD58WLZTPBMRUdM1YsQIjBgxQu4YdAfZm5vx48cjOzsbixYtQkZGBrp164bt27cbdxpOTU016fx69+6NdevW4bXXXsPf//53tGvXDps3b0anTp3keglERETUgMje3ADlpyKvbjPUnddbAYBx48Zh3LhxVk5FREREjRE3tBIREZFNYXNDRPVCxgMziaiRsNTnBJsbIrKqiiMcanOOCiJqmirOhXXnCfxqq0Hsc0NEtkupVMLDw8N4gUMnJyernVdFFEVotVqUlZXx8Oa7YK1qh/UyX11rJYoisrOz4eTkVOUlHmqDzQ0RWZ2vb/n11ioaHGuRJAmlpaVwdHTkienugrWqHdbLfPdSK4VCgcDAwHuuMZsbIrI6QRDQsmVLeHt7W/UaWTqdDnv37sWDDz7YKE94WJ9Yq9phvcx3L7Wyt7e3yJoxNjdEVG+USuU9b0u/2/x6vR4ODg78AroL1qp2WC/zNYRaccMhERER2RQ2N0RERGRT2NwQERGRTWly+9xUnCCooKDA4nPrdDqUlJSgoKCA22TvgrUyH2tlPtbKfKxV7bBe5rNWrSq+t8050V+Ta24KCwsBAAEBATInISIiotoqLCyEu7t7jWMEqYmdE10URVy/fh2urq4WP1dBQUEBAgICcPXqVbi5uVl0blvDWpmPtTIfa2U+1qp2WC/zWatWkiShsLAQfn5+dz1cvMmtuVEoFGjVqpVVn8PNzY1vfjOxVuZjrczHWpmPtaod1st81qjV3dbYVOAOxURERGRT2NwQERGRTWFzY0FqtRqxsbFQq9VyR2nwWCvzsVbmY63Mx1rVDutlvoZQqya3QzERERHZNq65ISIiIpvC5oaIiIhsCpsbIiIisilsbixk5cqVCAoKgoODAyIjI3Hw4EG5IzVIixcvhiAIJj/t27eXO1aDsHfvXowcORJ+fn4QBAGbN282uV+SJCxatAgtW7aEo6MjoqOj8eeff8oTVmZ3q9XTTz9d6X02dOhQecLKbOnSpbjvvvvg6uoKb29vjB49GufOnTMZU1ZWhlmzZqFFixZwcXHB2LFjkZmZKVNi+ZhTq/79+1d6bz377LMyJZbPp59+ii5duhjPZRMVFYVt27YZ75f7PcXmxgI2bNiAmJgYxMbG4ujRo+jatSuGDBmCrKwsuaM1SB07dkR6errx59dff5U7UoNQXFyMrl27YuXKlVXev2zZMnz00UdYtWoVDhw4AGdnZwwZMgRlZWX1nFR+d6sVAAwdOtTkffbdd9/VY8KGY8+ePZg1axb279+P+Ph46HQ6DB48GMXFxcYxc+fOxU8//YT//Oc/2LNnD65fv44xY8bImFoe5tQKAGbMmGHy3lq2bJlMieXTqlUrvPPOOzhy5AgOHz6Mhx56CKNGjcKpU6cANID3lET3LCIiQpo1a5bxtsFgkPz8/KSlS5fKmKphio2Nlbp27Sp3jAYPgLRp0ybjbVEUJV9fX+m9994zLsvLy5PUarX03XffyZCw4bizVpIkSZMnT5ZGjRolS56GLisrSwIg7dmzR5Kk8veRSqWS/vOf/xjHnDlzRgIgJSUlyRWzQbizVpIkSf369ZNefPFF+UI1YM2aNZO++OKLBvGe4pqbe6TVanHkyBFER0cblykUCkRHRyMpKUnGZA3Xn3/+CT8/P4SEhGDixIlITU2VO1KDl5KSgoyMDJP3mbu7OyIjI/k+q0ZiYiK8vb0RFhaG5557Djdu3JA7UoOQn58PAGjevDkA4MiRI9DpdCbvrfbt2yMwMLDJv7furFWFb7/9Fp6enujUqRMWLFiAkpISOeI1GAaDAevXr0dxcTGioqIaxHuqyV1bytJycnJgMBjg4+NjstzHxwdnz56VKVXDFRkZibi4OISFhSE9PR1LlixB37598ccff8DV1VXueA1WRkYGAFT5Pqu4j/4ydOhQjBkzBsHBwbh48SL+/ve/Y9iwYUhKSoJSqZQ7nmxEUcScOXPwwAMPoFOnTgDK31v29vbw8PAwGdvU31tV1QoAJkyYgNatW8PPzw8nTpzA/Pnzce7cOWzcuFHGtPI4efIkoqKiUFZWBhcXF2zatAkdOnRAcnKy7O8pNjdUr4YNG2b8d5cuXRAZGYnWrVvj+++/x7Rp02RMRrbkiSeeMP67c+fO6NKlC9q0aYPExEQMHDhQxmTymjVrFv744w/u52aG6mr1zDPPGP/duXNntGzZEgMHDsTFixfRpk2b+o4pq7CwMCQnJyM/Px8//PADJk+ejD179sgdCwB3KL5nnp6eUCqVlfYCz8zMhK+vr0ypGg8PDw+EhobiwoULckdp0CreS3yf1U1ISAg8PT2b9Pts9uzZ+Pnnn7F79260atXKuNzX1xdarRZ5eXkm45vye6u6WlUlMjISAJrke8ve3h5t27ZFz549sXTpUnTt2hUffvhhg3hPsbm5R/b29ujZsycSEhKMy0RRREJCAqKiomRM1jgUFRXh4sWLaNmypdxRGrTg4GD4+vqavM8KCgpw4MABvs/McO3aNdy4caNJvs8kScLs2bOxadMm7Nq1C8HBwSb39+zZEyqVyuS9de7cOaSmpja599bdalWV5ORkAGiS7607iaIIjUbTMN5T9bLbso1bv369pFarpbi4OOn06dPSM888I3l4eEgZGRlyR2twXnrpJSkxMVFKSUmRfvvtNyk6Olry9PSUsrKy5I4mu8LCQunYsWPSsWPHJADS8uXLpWPHjklXrlyRJEmS3nnnHcnDw0P68ccfpRMnTkijRo2SgoODpdLSUpmT17+aalVYWCjNmzdPSkpKklJSUqRffvlF6tGjh9SuXTuprKxM7uj17rnnnpPc3d2lxMREKT093fhTUlJiHPPss89KgYGB0q5du6TDhw9LUVFRUlRUlIyp5XG3Wl24cEF6/fXXpcOHD0spKSnSjz/+KIWEhEgPPvigzMnr36uvvirt2bNHSklJkU6cOCG9+uqrkiAI0s6dOyVJkv89xebGQj7++GMpMDBQsre3lyIiIqT9+/fLHalBGj9+vNSyZUvJ3t5e8vf3l8aPHy9duHBB7lgNwu7duyUAlX4mT54sSVL54eALFy6UfHx8JLVaLQ0cOFA6d+6cvKFlUlOtSkpKpMGDB0teXl6SSqWSWrduLc2YMaPJ/rFRVZ0ASGvWrDGOKS0tlWbOnCk1a9ZMcnJykh599FEpPT1dvtAyuVutUlNTpQcffFBq3ry5pFarpbZt20ovv/yylJ+fL29wGUydOlVq3bq1ZG9vL3l5eUkDBw40NjaSJP97ilcFJyIiIpvCfW6IiIjIprC5ISIiIpvC5oaIiIhsCpsbIiIisilsboiIiMimsLkhIiIim8LmhoiIiGwKmxsiIiKyKWxuiIiIyKawuSGiJu+pp57C22+/XefH33///fjvf/9rwUREdC/Y3BCRxWVkZOD5559HSEgI1Go1AgICMHLkSJOrBDcUx48fx9atW/HCCy8Yl/Xv3x+CIOCdd96pNH7EiBEQBAGLFy82Lnvttdfw6quvQhTF+ohMRHfB5oaILOry5cvo2bMndu3ahffeew8nT57E9u3bMWDAAMyaNUvueJV8/PHHGDduHFxcXEyWBwQEIC4uzmRZWloaEhIS0LJlS5Plw4YNQ2FhIbZt22btuERkBjY3RGRRM2fOhCAIOHjwIMaOHYvQ0FB07NgRMTEx2L9/v3FcamoqRo0aBRcXF7i5ueHxxx9HZmam8f7FixejW7du+PrrrxEUFAR3d3c88cQTKCwsNI4RRRHLli1D27ZtoVarERgYiLfeesvsrAaDAT/88ANGjhxZ6b6HH34YOTk5+O2334zLvvrqKwwePBje3t4mY5VKJYYPH47169eb/dxEZD1sbojIYnJzc7F9+3bMmjULzs7Ole738PAAUN6UjBo1Crm5udizZw/i4+Nx6dIljB8/3mT8xYsXsXnzZvz888/4+eefsWfPHpNNRQsWLMA777yDhQsX4vTp01i3bh18fHzMznvixAnk5+ejV69ele6zt7fHxIkTsWbNGuOyuLg4TJ06tcq5IiIisG/fPrOfm4ish80NEVnMhQsXIEkS2rdvX+O4hIQEnDx5EuvWrUPPnj0RGRmJtWvXYs+ePTh06JBxnCiKiIuLQ6dOndC3b1889dRTxv12CgsL8eGHH2LZsmWYPHky2rRpgz59+mD69Olm571y5QqUSmWlNTEVpk6diu+//x7FxcXYu3cv8vPz8fDDD1c51s/PD1evXuV+N0QNAJsbIrIYSZLMGnfmzBkEBAQgICDAuKxDhw7w8PDAmTNnjMuCgoLg6upqvN2yZUtkZWUZ59BoNBg4cGCd85aWlkKtVkMQhCrv79q1K9q1a4cffvgBq1evxlNPPQU7O7sqxzo6OkIURWg0mjrnISLLqPr/UiKiOmjXrh0EQcDZs2ctMp9KpTK5LQiCcc2Io6PjPc/v6emJkpISaLVa2NvbVzlm6tSpWLlyJU6fPo2DBw9WO1dubi6cnZ0tkouI7g3X3BCRxTRv3hxDhgzBypUrUVxcXOn+vLw8AEB4eDiuXr2Kq1evGu87ffo08vLy0KFDB7Oeq127dnB0dLynw8u7detmfO7qTJgwASdPnkSnTp1qzPbHH3+ge/fudc5CRJbD5oaILGrlypUwGAyIiIjAf//7X/z55584c+YMPvroI0RFRQEAoqOj0blzZ0ycOBFHjx7FwYMHMWnSJPTr16/KnXur4uDggPnz5+OVV17B2rVrcfHiRezfvx9ffvmlcczAgQPxySefVDuHl5cXevTogV9//bXaMc2aNUN6evpdm6h9+/Zh8ODBZmUnIutic0NEFhUSEoKjR49iwIABeOmll9CpUycMGjQICQkJ+PTTTwGUb1768ccf0axZMzz44IOIjo5GSEgINmzYUKvnWrhwIV566SUsWrQI4eHhGD9+vHGfHKD8aKucnJwa55g+fTq+/fbbGsd4eHhUefRXhbS0NPz++++YMmVKrfITkXUIkrl7ABIR2aDS0lKEhYVhw4YNxjVLtTV//nzcvHkTn332mYXTEVFdcIdiImrSHB0dsXbt2ruu4amJt7c3YmJiLJiKiO4F19wQERGRTeE+N0RERGRT2NwQERGRTWFzQ0RERDaFzQ0RERHZFDY3REREZFPY3BAREZFNYXNDRERENoXNDREREdkUNjdERERkU/4fzDW2Zw5EjZ8AAAAASUVORK5CYII="]},"metadata":{}}],"source":["k_on, k_off = res.x\n","k_on = 10**k_on # transform to linear space\n","k_off = 10**k_off # transform to linear space \n","#P0 = ...#already set.\n","PL0 = 0\n","L0 = L1_0+L2_0\n","y0 = [P0, L0, PL0]\n","\n","y = odeint(rate_equations, y0, t, args=(k_on, k_off))\n","\n","plt.plot(t, observed, label=\"Multi-species system\")\n","plt.plot(t, y[:,-1], linestyle='--', label='Fitted kinetic model, P+L<->PL')\n","plt.xlabel('Conc. (M)')\n","plt.ylabel('Time (s)')\n","plt.legend()\n","plt.grid()"],"metadata":{}},{"id":"196aff99-b12c-4d6e-afc1-f19fb431fcd9","cell_type":"markdown","source":["after all that, this is our apparent Kd from our 'experiment', in Molar:"],"metadata":{},"attachments":{}},{"id":"e1c4a220-b64a-4df0-8904-57e780fae375","cell_type":"code","execution_count":12,"outputs":[{"output_type":"stream","name":"stdout","text":["1.1174941097085943e-07\n"]}],"source":["observed_kd = 1/(k_on/k_off)\n","print(observed_kd)"],"metadata":{}},{"id":"19385dd9-c6cd-486b-8610-fab0a6143c85","cell_type":"markdown","source":["# now compare our observed Ki to the master equation Kd.\n","\n","the master equation says we sum the equilibrium binding constants of the ligand species, weighted by their fraction in the unbound population.\n","\n","i.e. `K_eq = f1*keq1 + f2*keq2 + ....`"],"metadata":{},"attachments":{}},{"id":"2eb751f8-f45a-462b-8845-cd3502052471","cell_type":"code","execution_count":13,"outputs":[{"output_type":"execute_result","execution_count":null,"data":{"text/plain":["9.546538414232915e-08"]},"metadata":{}}],"source":["#combined K_eq:\n","\n","true_k_eq = f1 * true_taut1_k_eq + f2 * true_taut2_k_eq\n","\n","# convert to K_i:\n","true_kd = 1/true_k_eq\n","true_kd"],"metadata":{}},{"id":"d23584b5-8602-42ce-b111-38698cb81323","cell_type":"markdown","source":["the master equation says our combined Kd should be something like 95 nM. Note that this is a pretty big drop from the true Ki of tautomer 2, which was 5 nM, but it's also substantially _better_ than our tautomer 1, whch was 5 µM!"],"metadata":{},"attachments":{}},{"id":"434167cc-e4a5-49d6-a76b-34311c4a50ff","cell_type":"code","execution_count":14,"outputs":[{"output_type":"stream","name":"stdout","text":["Combined Kd using the master equation method, in µM:\n0.0955\nObserved Kd by fitting an ODE model, in µM:\n0.1117\n"]}],"source":["print(\"Combined Kd using the master equation method, in µM:\")\n","print(np.around(true_kd*1e6, 4))\n","print(\"Observed Kd by fitting an ODE model, in µM:\")\n","print(np.around(observed_kd*1e6, 4))"],"metadata":{}},{"id":"e6388da7-533d-45ac-b128-34148b7c8170","cell_type":"code","execution_count":15,"outputs":[{"output_type":"stream","name":"stdout","text":["Fractional difference in master equation to our observed Kd:\n"]},{"output_type":"execute_result","execution_count":null,"data":{"text/plain":["1.17057519827556"]},"metadata":{}}],"source":["print('Fractional difference in master equation to our observed Kd:')\n","observed_kd/true_kd"],"metadata":{}},{"id":"b8dda1db-dab4-4406-8187-9df247a18796","cell_type":"markdown","source":["pretty close! the master equation and our experimental observed Kd were within about 20%."],"metadata":{},"attachments":{}},{"id":"cfaae18e-5158-41a4-b32c-b69b5c616cc5","cell_type":"markdown","source":["finally: we didn't need to go to all the trouble of fitting the on-rate/off-rates to get a K_eq, but it's fun because that's what you might do in SPR. In a biochemical experiment we might also just measure the equilibrium state concentrations - because K_eq is also `[P][L]/[PL]` at equilibrium. Here's the easy way:"],"metadata":{},"attachments":{}},{"id":"abbc9ed7-3918-41f7-9123-3e9106e58d88","cell_type":"code","execution_count":16,"outputs":[{"output_type":"stream","name":"stdout","text":["Combined Ki using the master equation method, in µM:\n0.0955\nObserved Ki by fitting an ODE model, in µM:\n0.1076\n"]}],"source":["\n","final_state = y[-1]\n","observed_kd = (final_state[0]*final_state[1]) / (final_state[2])\n","\n","print(\"Combined Ki using the master equation method, in µM:\")\n","print(np.around(true_kd*1e6, 4))\n","print(\"Observed Ki by fitting an ODE model, in µM:\")\n","print(np.around(observed_kd*1e6, 4))"],"metadata":{}},{"id":"5c3a5e10-a47c-4d44-a38a-f02f3ceb1e12","cell_type":"markdown","source":["it's actually a bit closer :)"],"metadata":{},"attachments":{}},{"id":"53da97b5-d622-4a64-984c-0a71c1d35856","cell_type":"code","execution_count":17,"outputs":[{"output_type":"stream","name":"stdout","text":["Fractional difference in master equation to our observed Ki:\n"]},{"output_type":"execute_result","execution_count":null,"data":{"text/plain":["1.1268707523301031"]},"metadata":{}}],"source":["print('Fractional difference in master equation to our observed Ki:')\n","observed_kd/true_kd"],"metadata":{}},{"id":"6403b3c3-cde1-4eac-af61-1906be5c93c2","cell_type":"markdown","source":["# conclusion. \n","\n","so it looks like the master equation is pretty good. If it's a simulation, with no noise, why doesn't it agree perfectly? It's not clear whether the simulation is imperfect (certainly plausible) or whether the master equation is imperfect (seems fine to me), _or_ if the assumptions I made about kinetic rates mean the applicability domain is a bit off.\n","\n","And, to answer my own question: If I predicted a ligand is very potent, but it was a minor tautomer, then it's probably not a huge deal if it's at least a 1-in-20 occupancy tautomer. "],"metadata":{},"attachments":{}},{"id":"0cf81698-15c5-4b05-aac5-e3abf35d34ff","cell_type":"markdown","source":["# tldr; how to use this:\n","if you don't care for the modelling aspect, here's a quick heuristic using orders of magnitude. Let's use the situation where you have one active tautomer/protomer of interest at 50 nM, and the other one is functionally inactive - let's call it 500 µM. For most populations for tautomer 1 (the 'f' value), your observed potency is going to be _pretty_ close to 50 nM. It's only once you get to about ~10% occupancy of the potent tautomer that you lose a full log unit of potency. And, when you get to ~1% occupancy you lose another log. So it's more or less powers of ten. \n","\n","the same math works for a single ligand species binding to an active conformation of a protein that is only 10% populated, or 1%, and so on..."],"metadata":{},"attachments":{}},{"id":"12bdbb70-c866-4561-b8a0-965eddcd3cf1","cell_type":"code","execution_count":18,"outputs":[{"output_type":"stream","name":"stdout","text":["Observed Ki: 7.255\n"]}],"source":["true_taut1_kd = 50/1e9 #50 nanomolar\n","true_taut2_kd = 500/1e6 #500 micromolar\n","\n","f1 = 0.9 #lots of the potent tautomer. observed Ki should be a little bit worse than 50 nM (which is pkd=7.3)\n","f2 = 1-f2\n","\n","keq = f1*(1/true_taut1_kd) + f1*(1/true_taut2_kd)\n","print('Observed Ki:', np.around(-np.log10(1/keq), 3, ))\n"],"metadata":{}},{"id":"edbbffcc-bebe-499f-8680-7052c1193ed1","cell_type":"code","execution_count":19,"outputs":[{"output_type":"stream","name":"stdout","text":["Observed Ki: 6.301\n"]}],"source":["f1 = 0.1 # 1 in 10 ratio of potent tautomer. observed Ki should be near 500 nM (which is pkd=6.3)\n","f2 = 1-f1\n","\n","keq = f1*(1/true_taut1_kd) + f1*(1/true_taut2_kd)\n","print('Observed Ki:', np.around(-np.log10(1/keq), 3, ))\n"],"metadata":{}},{"id":"8d6431dd-b35d-48f3-9da9-c8e154052e05","cell_type":"code","execution_count":20,"outputs":[{"output_type":"stream","name":"stdout","text":["Observed Ki: 5.301\n"]}],"source":["f1 = 0.01 # 1 in 100 ratio of potent tautomer. Observed Ki should be about 5 µM\n","f2 = 1-f1\n","\n","keq = f1*(1/true_taut1_kd) + f1*(1/true_taut2_kd)\n","print('Observed Ki:', np.around(-np.log10(1/keq), 3, ))\n"],"metadata":{}},{"id":"ebb70a6d-27ee-43bd-975c-19b23a8daaae","cell_type":"code","execution_count":21,"outputs":[{"output_type":"stream","name":"stdout","text":["K_i for tautomer 1 (in Molar): 5e-08\nK_i for tautomer 2 (in Molar): 0.0005\n"]},{"output_type":"display_data","data":{"text/plain":["<Figure size 640x480 with 1 Axes>"],"image/png":["iVBORw0KGgoAAAANSUhEUgAAAkIAAAG1CAYAAAAV2Js8AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjkuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy80BEi2AAAACXBIWXMAAA9hAAAPYQGoP6dpAABkGklEQVR4nO3deVxU9f4/8NfMMCzDqqIgyKLiRiq4gbug4NbVzBbLFjKzrqWVlN361i3r3puVppZRZt0yK8uyXMrcFTGXXNFUEFFEFERRYQQUB+b8/uDKL2SZM4fDzBnO6/l4+LiXOe/P+bzB98XPPfP+zEcjCIIAIiIiIhXS2jsBIiIiInvhQoiIiIhUiwshIiIiUi0uhIiIiEi1uBAiIiIi1eJCiIiIiFSLCyEiIiJSLS6EiIiISLWc7J2A0pnNZuTm5sLT0xMajcbe6RAREZEIgiDg2rVrCAgIgFZb93MfLoQsyM3NRVBQkL3TICIiIglycnLQpk2bOq9zIWSBp6cngMofpJeXV43rJpMJGzduxPDhw6HX62W5pmS2ylvOeaTey9pxYuPFxFmKaWq1paa6kjJWrtpiXSl/LkesK0sx9qoro9GIoKCgqn/H68KFkAW33g7z8vKqcyFkMBjg5eVV61+wlGtKZqu85ZxH6r2sHSc2XkycpZimVltqqispY+WqLdaV8udyxLqyFGPvurLU1sKFkEgmkwkmk6nW1//6n3JcUzJb5S3nPFLvZe04sfFi4izFNLXaUlNdSRkrV22xrpQ/lyPWlaUYe9WV2HtqePp87ZKSkpCUlISKigpkZGRg2bJlMBgM9k6LiIiIRCgtLcXEiRNRVFRU6zs6t3AhZIHRaIS3tzcKCgrqfGts06ZNiI+Pr/WRn5RrSmarvOWcR+q9rB0nNl5MnKWYplZbaqorKWPlqi3WlfLncsS6shRjr7oyGo3w9fW1uBDiW2Mi6fX6ev+S6rsu9ZqS2SpvOeeRei9rx4mNFxPXWHWnVGqqKylj5aot1pXy53LEurIUY+u6Ens/fqAiERERqRYXQkRERKRafGtMJO4aq6Sm3T1K3YFh6boj1paa6krKWO4ak4a7xuSJ564xleKuMSIiIsfFXWMy4a6x6tS0u0epOzAsXXfE2lJTXUkZy11j0nDXmDzx3DVGALhr7HZq2t2j1B0Ylq47Ym2pqa6kjOWuMWm4a0yeeO4aIyIiImpiuBAiIiIi1eJbYyJx11glNe3uUeoODEvXHbG21FRXUsZy15g03DUmTzx3jakUd40RERE5Lu4akwl3jVWnpt09St2BYem6I9aWmupKyljuGpOGu8bkieeuMQLAXWO3U9PuHqXuwLB03RFrS011JWUsd41Jw11j8sRz1xgRERFRE8OFEBEREakWF0JERESkWlwIERERkWqxWVokfo5QJTV93otSP5PD0nVHrC011ZWUsfwcIWn4OULyxPNzhFSKnyNERETkuPg5QjLh5whVp6bPe1HqZ3JYuu6ItaWmupIylp8jJA0/R0ieeH6OEAHg5wjdTk2f96LUz+SwdN0Ra0tNdSVlLD9HSBp+jpA88fwcISIiIqImhgshIiIiUi0uhIiIiEi1uBAiIiIi1eJCiIiIiFSLCyEiIiJSLS6EiIiISLX4OUIi8YiNSmo6CkGpH1dv6boj1paa6krKWB6xIQ2P2JAnnkdsqBSP2CAiInJcPGJDJjxiozo1HYWg1I+rt3TdEWtLTXUlZSyP2JCGR2zIE88jNggAj9i4nZqOQlDqx9Vbuu6ItaWmupIylkdsSMMjNuSJ5xEbRERERE0MF0JERESkWlwIERERkWpxIURERESqxYUQERERqRYXQkRERKRaXAgRERGRanEhRERERKrFhRARERGpFhdCREREpFpcCBEREZFq8awxkUwmE0wmU62v//U/5bimZLbKW855pN7L2nFi48XEWYpparWlprqSMlau2mJdKX8uR6wrSzH2qiux9+Tp83VISkpCUlISKioqkJGRgWXLlsFgMNg7LSIiIhKhtLQUEydOtHj6PBdCFhiNRnh7e6OgoKDWH6TJZMKmTZsQHx9f46RbqdeUzFZ5yzmP1HtZO05svJg4SzFNrbbUVFdSxspVW6wr5c/liHVlKcZedWU0GuHr62txIcS3xkTS6/X1/iXVd13qNSWzVd5yziP1XtaOExsvJq6x6k6p1FRXUsbKVVusK+XP5Yh1ZSnG1nUl9n5sliYiIiLV4kKIiIiIVIsLISIiIlItLoSIiIhItbgQIiIiItXiQoiIiIhUiwshIiIiUi0uhIiIiEi1uBAiIiIi1eJCiIiIiFSLCyEiIiJSLS6EiIiISLW4ECIiIiLV4kKIiIiIVIsLISIiIlItLoSIiIhItVSzECotLUVISAhefPFFe6dCRERECqGahdB//vMf9O3b195pEBERkYKoYiF08uRJpKenY9SoUfZOhYiIiBTE7guhlJQUjBkzBgEBAdBoNFi1alWNmKSkJISGhsLV1RXR0dHYu3evVXO8+OKLmD17tkwZExERUVNh94VQSUkJIiIikJSUVOv15cuXIzExEW+88QYOHjyIiIgIjBgxAhcvXqyKiYyMRNeuXWv8yc3NxerVq9GxY0d07NjRVt8SEREROQgneycwatSoet+ymjdvHqZMmYJJkyYBABYtWoS1a9fiiy++wMsvvwwASE1NrXP8nj178P333+PHH39EcXExTCYTvLy88Prrr9caX1ZWhrKysqqvjUYjAMBkMsFkMtWIv/WanNeUzFZ5yzmP1HtZO05svJg4SzFNrbbUVFdSxspVW6wr5c/liHVlKcZedSX2nhpBEATZZ5dIo9Fg5cqVGDduHADg5s2bMBgMWLFiRdVrAJCQkIDCwkKsXr3aqvsvWbIER48exdy5c+uMmTVrFt58880ary9btgwGg8Gq+YiIiMg+SktLMXHiRBQVFcHLy6vOOLs/EapPQUEBKioq4OfnV+11Pz8/pKenN8qcr7zyChITE6u+NhqNCAoKwvDhw2v9QZpMJmzatAnx8fHQ6/WyXFMyW+Ut5zxS72XtOLHxYuIsxTS12lJTXUkZK1dtsa6UP5cj1pWlGHvV1a13dCxR9EJIbo899pjFGBcXF7i4uNR4Xa/X1/uXVN91qdeUzFZ5yzmP1HtZO05svJi4xqo7pVJTXUkZK1dtsa6UP5cj1pWlGFvXldj7KXoh5OvrC51Oh/z8/Gqv5+fnw9/f36a5sEeokpp6OZT6frul645YW2qqKylj2SMkDXuE5Ilnj5AN3d4jBADR0dGIiorCwoULAQBmsxnBwcGYNm1aVbN0Y0hKSkJSUhIqKiqQkZHBHiEiIiIHIrZHyO4LoeLiYmRmZgIAevTogXnz5iE2NhbNmzdHcHAwli9fjoSEBHz66aeIiorCggUL8MMPPyA9Pb1G71BjMBqN8Pb2RkFBAXuEoK5eDqW+327puiPWlprqSspY9ghJwx4heeIduUfI19dX+c3S+/fvR2xsbNXXtxqVExISsGTJEkyYMAGXLl3C66+/jgsXLiAyMhLr16+3ySLor9gjVJ2aejmU+n67peuOWFtqqispY9kjJA17hOSJZ49QI4mJiYGlh1LTpk3DtGnTbJRR7dgjVElNvRxKfb/d0nVHrC011ZWUsewRkoY9QvLEs0dIpdgjRERE5LgcpkdI6dgjVJ2aejmU+n67peuOWFtqqispY9kjJA17hOSJZ48QAWCP0O3U1Muh1PfbLV13xNpSU11JGcseIWnYIyRPfFPtEbL7oatERERE9sInQiKxWbqSmppaldp4aOm6I9aWmupKylg2S0vDZml54tksrVJsliYiInJcbJaWCZulq1NTU6tSGw8tXXfE2lJTXUkZy2ZpadgsLU88m6UJAJulb6emplalNh5auu6ItaWmupIyls3S0rBZWp54NksTERERNTFcCBEREZFq8a0xkbhrrJKadvcodQeGpeuOWFtqqispY7lrTBruGpMnnrvGVIq7xoiIiBwXd43JhLvGqlPT7h6l7sCwdN0Ra0tNdSVlLHeNScNdY/LEc9cYAeCusdupaXePUndgWLruiLWlprqSMpa7xqThrjF54rlrjIiIiKiJ4RMhkUpKSqDT6Wq8bjKZcOPGDZSUlNT6yE/KNSWzVd5yziP1XtaOExsvJs5STFOrLTXVlZSxctUW60r5czliXVmKsVddlZSUiIrjQkikgIAAe6dAREREMuNbY3VISkpCeHg4+vTpY+9UiIiIqJFw15gFt3aNZWdn17lrbOvWrRg6dGitj/ykXFMyW+Ut5zxS72XtOLHxYuIsxTS12lJTXUkZK1dtsa6UP5cj1pWlGHvVldFoREhICHeNySXLaIaHYL7tVQ0qyoE8kyuyjIDOqXJNqdFUXi0vBy6YXJF1DdA7VV9vlpcDRYIrfHx8HOaXClBZtK6ujZ+3nPNIvZe148TGi4mzFFPfdVv9HclJTXUlZaxctcW6Uv5cjlhXlmLsVVdarbg3vbgQEumR/+6D1qWuD1R0woKje+u8Nr+ea8nX9uOlkV0QGeTT8CSJiIjIKlwIiRTU3A1OrjUXQmazgNLSUhgMBmhuPQq6dU0QcL20FG4GA267BEEA8gpLsevUFYxL2on4cD+8MLwjOvvX/fiOiIiI5MWFkEjrnhtcZ4/Qb7/9htGjB9X6yK++a1///BuOIhirUnOx6Xg+NqflY0z3AMyI74i2vu6N+v0QERERd43ZVQtX4N3xXbFxxhDc2a01BAFYczgXcfO24+WfjiC38Lq9UyQiImrS+ERIJJOp8U6fD2nmggX3d8OUgSGYvyUT2zMK8P2+HPx08BwmRgVh6uC2aOHhIue3I1l935NS55F6L2vHiY0XE2cpRmrdKZWa6krKWLlqi3Wl/Lkcsa4sxdirrsTek9vn62DP0+dPG4G1OTpkGisbi5y1Aoa0FjA0wAwDl65EREQW8fR5mdjr9HlBELDz1BXM23wSf543AgC8XJ3wxMBQPNo3GO4u9lkRWcpbifNIvZe148TGi4mzFNOQ2lIiNdWVlLFy1RbrSvlzOWJdWYqxV13x9HmZWToZV+qpuvVdi+3ij5jOfth4PB/vbzyBjPxizNuciaV7zuLpmDBMjA6Gq77m+We2YOnnocR5pN7L2nFi48XENVbdKZWa6krKWLlqi3Wl/Lkcsa4sxdi6rsTej83SCqfRaDDiDn+se24wFkyIREgLAwqKb+KtX49j6NxkfL/3LMorbv+gRyIiIhKDCyEHodNqMK5HIDYnDsHbd3eDv5crcotu4OWf/0T8/BSsTj0Ps5nvchIREVmDCyEHo9dpMTE6GMkzY/DanV3Qwt0ZWQUleO77VIz+cAc2Hc8H276IiIjE4ULIQbnqdXhiUDukvBSLF4d3hKerE9IvXMOUpftx98e7sDOzwN4pEhERKR4XQg7O3cUJ04Z2wI6XYvF0THu46XVIzSnEQ5//gQcX78GB7Kv2TpGIiEixuBBqInwMznhpZGdsfykGj/UPhbNOi92nL+OeT3Zh8pJ9OJ5rtHeKREREisOFUBPTytMVs8begW0zYzChdxB0Wg22pF/E6A93YNqygzh9qdjeKRIRESkGP0dIpMY8YqMxtHJ3wr/v6oLJA4LxwdZTWPvnBfx6JA/rjl7A3ZEBmBbbDoE+blbfV01HISj14+otXedRCLaZxxGPQmBdKX8uR6wrSzE8YsNB2fOIjcZwvgT4LUeLo1crHwLqNAIG+AmIDzTDy9nOyREREcmMR2zIxF5HbDSWQzmFmL85E7tPXwEAuOm1eLRvCJ4YGAofg3wfyd5QSjgKQakfV2/pOo9CsM08jngUAutK+XM5Yl1ZiuERG02EPY7YaAxR7VriuydbYmdmAeZsOIHUnEJ8uiMLy/bm4MnB7TBpYFt4iDjHTE1HISj14+otXedRCLaZxxGPQmBdKX8uR6wrSzE8YoMUZUCYL1Y+3R+fP9obnf09ca2sHO9vysDg97bh8x2nccNUYe8UiYiIGh0XQiqm0WgQF+6H354dhA8f7IG2vu64UnIT/16bhpg5yVj2x1mYeI4ZERE1YVwIEbRaDcZGBGDTjMF4955uCPB2xQXjDfzfyj8RN287Vh06jwqeY0ZERE0QF0JUxUmnxYQ+wdj6YgzeGBMOXw9nZF8uxfPLUzHqgxSsP3qB55gREVGTwmZpqsFVr8OkAW1xf+8gLNl1Bp9uP4WM/GL8/ZsD6B7ohYHeGoy2d5JEREQy4BMhqpO7ixOeiQ3Djn8MxbTYMBicdThy3oiPj+sw6asDOHq+yN4pEhERNQgXQmSRt5seL47ohJSXYvFo32DoNAJ+z7yMvy38Hc99fwhnL5faO0UiIiJJuBAi0Xw9XPDPOzvj/yIrMKa7PwBgdWouhs1Lxqw1x3C5uMzOGRIREVmHCyGymq8rMO++7vh1+kAM6uALU4WAJbvOYMicZHy45SRKysrtnSIREZEoXAiRZF0DvfH15Gh8Mzka3QK9UVxWjnmbMjBkTjK+3pPNzyAiIiLF40KIGmxgB1+sfmYAFj7YA8HNDSgoLsM/Vx3F8Pkp+O3PPG65JyIixeL2eZFMJhNMJlOtr//1P+W4pmT15T0yvCWGdmyBHw6cw8Jtp5BVUIKnvz2I7m288NLwjohu21yWeeTMWc5xYuPFxFmKaWq1ZauclVBXUsbKVVusK+XP5Yh1ZSnGXnUl9p48fb4OSUlJSEpKQkVFBTIyMrBs2TIYDAZ7p+UwblQA23I12JqrxU2zBgDQxceMMcFmBLrbOTkiImrySktLMXHiRIunz3MhZIHRaIS3tzcKCgpq/UGaTCZs2rQJ8fHxNU66lXpNyazNu6C4DEnJp/H9vnMoNwvQaIC7urfGc8PC0KaZm2zzyJmz1HFi48XEWYpparVlq5yVUFdSxspVW6wr5c/liHVlKcZedWU0GuHr62txIcS3xkTS6/X1/iXVd13qNSUTm3frZnr8++7ueGJQe8zdeAK/HsnDqsN5+O1oPh7pF4JnYsPQ3N25wfPImXNDx4mNFxPXWHWnVLbKWQl1JWWsXLXFulL+XI5YV5ZibF1XYu/HZmmyiVBfd3w0sSfWTBuA/u1b4GaFGf/9PQtD3tuGpG2ZuH6zwt4pEhGRCnEhRDbVvY0Pvn0iGksfj0J4ay9cKyvHnA0nMGTONny39yzKueWeiIhsiAshsjmNRoPBHVvi1+kD8cEDkWjTzA0Xr5XhlZ//xPAFPOWeiIhshz1CZDdarQZ3RQZiZFd/LPvjLBZuzcTpSyX4+zcHEBnkjcF197YRERHJgk+EyO5cnHSYNKAtts+MwbNDw+Cm1yE1pwgfHnPCk98cxIkL1+ydIhERNVFcCJFieLrqkTi8E7bPjMHEqDbQQsC2EwUY+UEKXvzxMM4XXrd3ikRE1MSIemtszZo1om84duxYyckQAUArL1e8OSYcbW+ewQFTINYfy8eKA+ew5nAuJvUPxdSY9vAx1L3lnoiISCxRC6Fx48ZV+1qj0VRrZtVoNFX/vaKC26BJHq3cgIX3ROBoXjHeWZeOP7Ku4NOU0/hu71lMjQnDpAGhcNXr7J0mERE5MFFvjZnN5qo/GzduRGRkJNatW4fCwkIUFhbit99+Q8+ePbF+/frGzpdUqEdwM3z/ZF98OakPOvt7wnijHO+uT0fMnGT8sC+HW+6JiEgyq3eNPf/881i0aBEGDhxY9dqIESNgMBjw5JNPIi0tTdYEiYDKp46xnVphcIeWWJ16Hu9vzMD5wut46acj+GzHabw0sjPiurSq9nSSiIjIEqubpU+dOgUfH58ar3t7e+PMmTMypERUN51Wg/E922DLC0Pw2p1d4GPQ4+TFYkxZuh/3LdqN/Weu2DtFIiJyIFYvhPr06YPExETk5+dXvZafn4+ZM2ciKipK1uSI6uKq1+GJQe2Q8lIsno5pD1e9Fvuzr+LeRbsxZel+nMznlnsiIrLM6oXQF198gby8PAQHByMsLAxhYWEIDg7G+fPn8fnnnzdGjkR18nLV46WRnZH8YiwejAqCVgNsOp6PEQtS8I8VR5BXxC33RERUN6t7hMLCwnDkyBFs2rQJ6enpAIAuXbogLi6O/RlkN/7erpg9vjsmD2yHORvSseFYPpbvz8Gq1PNI6BeMtuX2zpCIiJRI9EIoJSUFgwcPBlDZuDp8+HAMHz68Wsz06dOxcOFCeTMkskJYKw98+khvHMi+infWpWHfmatYvOMMDE46XPPNRsKAtnBx4pZ7IiKqJPqtsbFjxyI1NbXO69OnT8dXX30lR05EDdYrpBl+eKof/pvQGx1auaO0XIO3151A3LztWHM4l4e6EhERACsWQk888QRGjhyJzMzMGteee+45fPnll/jll19kTU4uoaGh6N69OyIjIxEbG2vvdMhGNBoNhnXxw5qn++GBdhVo5emCnCvX8ex3hzAuaSf2nL5s7xSJiMjORL81NnfuXFy5cgVxcXHYtWsXAgICAFR+rtDnn3+OX3/9FUOGDGm0RBtq165d8PDwsHcaZAdOOi36+Ql45aEBWLrnHBZtP4XD54rwwOI9iOvSCv8Y2Rkd/DztnSYREdmBVbvGPv/8c/Ts2RNxcXG4fPkyEhMTsXjxYqxZs4ZPWkjxDM5OmD6sA5JnxuKRviHQaTXYnHYRIxak4JWf/8RF4w17p0hERDZm1UJIq9Xi+++/R2BgILp06YJPP/0Ua9aswbBhwyQnkJKSgjFjxiAgIAAajQarVq2qEZOUlITQ0FC4uroiOjoae/futWoOjUaDIUOGoE+fPvj2228l50pNQ0tPF/xrXFdsnDEYw8P9YBaA7/aeRczcZMzflIGSMm4xIyJSC9FvjX344YdV/z0mJgY7duzAiBEjcPz4cRw/frzq2rPPPmtVAiUlJYiIiMDjjz+O8ePH17i+fPlyJCYmYtGiRYiOjsaCBQswYsQInDhxAq1atQIAREZGory85j9eGzduREBAAH7//XcEBgYiLy8PcXFx6NatG7p3725VntT0tG/pgcWP9sa+M1fw9m9pOHS2EB9sOYlv/ziLGfEdMD7C394pEhFRIxO9EJo/f361r1u3bo0jR47gyJEjVa9pNBqrF0KjRo3CqFGj6rw+b948TJkyBZMmTQIALFq0CGvXrsUXX3yBl19+GQDq3c0GAIGBgVU5jx49GgcPHqxzIVRWVoaysrKqr41GIwDAZDLBZDLViL/1mpzXlMxWecs5j6V7RQZ6YvkTfbD+WD7mbjqJs1eu49WVR/HfHacxtIUGcTdvypqzmDhLMU2ttppiXck5Vq7aYl0pfy5HrCtLMfaqK7H31AgK2kes0WiwcuVKjBs3DgBw8+ZNGAwGrFixouo1AEhISEBhYSFWr15t8Z4lJSUwm83w9PREcXExhgwZgkWLFqFPnz61xs+aNQtvvvlmjdeXLVsGg8Eg6fsix1FuBnbla7D+nBYl5ZUfENreU8BdIRUIYT81EZHDKC0txcSJE1FUVAQvL68646z+ZGlbKigoQEVFBfz8/Kq97ufnV/Wp1pbk5+fj7rvvBgBUVFRgypQpdS6CAOCVV15BYmJi1ddGoxFBQUEYPnx4rT9Ik8mETZs2IT4+Hnq9XpZrSmarvOWcx9p7jQXw6g0TPkk+hSW7snHqmgbzjjrhzq7+mBEfhpDmtS+Ixc4jJs5STFOrLTXUVUPGylVbrCvlz+WIdWUpxl51desdHUsUvRCSQ7t27XD48GHR8S4uLnBxcanxul6vr/cvqb7rUq8pma3ylnMea+7VXF95hlmb66dxWAjGytRcrD16ARvT8vFw3xA8O7QDmrk7N2geMXGNVXdK1dTrqqFj5aot1pXy53LEurIUY+u6Ens/RS+EfH19odPpqp10D1Q+5fH3t20jK3uEKqmpl8NkMsHHBfh3fCdM6h+C9zZkYEfmZXy58wxWHDiHpwa1RUK/YLjqdVbNwx6hmtRUV1LGskdIGvYIyRPPHiEbur1HCACio6MRFRVVdYaZ2WxGcHAwpk2bVtUs3RiSkpKQlJSEiooKZGRksEeIAADphRqsydbifGll/5CPs4A7g83o7StAyzOHiYgUQ2yPkN0XQsXFxVXHdvTo0QPz5s1DbGwsmjdvjuDgYCxfvhwJCQn49NNPERUVhQULFuCHH35Aenp6jd6hxmA0GuHt7Y2CggL2CEFdvRx1jTObBaw5kod5mzORV1T5IYxd/D3xwrB2KDl9gD1CEqiprqSMZY+QNOwRkifekXuEfH195WmWFttwBKDeyWqzf//+ap9KfatROSEhAUuWLMGECRNw6dIlvP7667hw4QIiIyOxfv16myyC/oo9QtWpqZejtnH39QnBmMg2WLLrDJK2ZSLtwjU88e1hdPbWol3PG+gWZPnpIXuEalJTXUkZyx4hadgjJE+8qnuEfHx8oNGIe+5fUVEhKu6WmJgYiyeBT5s2DdOmTbPqvnJjj1AlNfVyWBqnAzC5fzDujvDHJ9tP45s/cpBepMXYpN24u0cAnh8WhtberpLyYS+H8udxxF4O1pXy53LEurIU0yR6hLZv317138+cOYOXX34Zjz32GPr16wcA2L17N7766ivMnj0bCQkJElNWFvYIkbUKbgC/ntXi0OXKk2v0GgFDAgTEBZjhpuhtCURETU+j9QgNGzYMTzzxBB588MFqry9btgyLFy9GcnKypISVij1C1ampl0Pq++2tukTh/S2nsT+7EADQzKDHtNj2eKB3Gzg7adkjVAs11ZWUsewRkoY9QvLEs0foNrt378aiRYtqvN67d2888cQT1t7OYbBHqDo19XJYO653W1/8+Hd/bE67iHfWpeHUpRL8a206vt5zFi+N7Iy4Ti1E35e9HMqfxxF7OVhXyp/LEevKUoxSe4SsOn0eAIKCgvDZZ5/VeP3zzz9HUFCQtbcjapI0Gg3iw/2w4fnB+M/dXeHr4YIzl0vx9LcHcf9ne3Fa/P4DIiJqRFY/EZo/fz7uuecerFu3DtHR0QCAvXv34uTJk/jpp59kT1Ap2CxdSU1NrXI1Ht7fMwCj72iFL3aewee/n0FqThFS4YRj3x7EzOGd0K6lu9VzN7XaUlNdSRnLZmlp2CwtTzybpWuRk5ODTz75pOq8ry5duuDvf/97k3oixGZpagxFN4H1OVrsvqiBAA20ENDPT8DINmZ41X5iBxERSeAwH6iodGyWrk5NTa2N2Xj49epN2HPdD9syLgMA3J11mDKoLSb1D4bB2YlNrQ4wjyM2tbKulD+XI9aVpZgm1ywNADt27MCnn36K06dP48cff0RgYCC+/vprtG3bFgMHDpSctJKxWbo6NTW1Nkbjob8BWHxvLxzIMWL2b2k4fK4IC7Zk4rt9OUiM74i7uvuLuldTqy011ZWUsWyWlobN0vLEs1n6f3766SeMGDECbm5uOHjwIMrKygAARUVFePvtt629HZGq9W3XAiufHoAPH+yBoOZuyDeW4R8//YkxSbtw7KrG4oeNEhFRw1i9EPr3v/+NRYsW4bPPPqu22howYAAOHjwoa3JEaqDVajA2IgCbE4fgtTu7wNtNj5MXS7A4XYfHlhzA0fNF9k6RiKjJsvqtsRMnTmDw4ME1Xvf29kZhYaEcOSkSd41VUtPuHlvvwNACSOgbhHER/vh4Wya+2nMWu05fwZiPfse4iNaYEdeh6siOplZbaqorKWO5a0wa7hqTJ567xm7Trl07LF68GHFxcfD09MThw4fRrl07LF26FO+88w6OHz8uKWGl4a4xsrfLN4C1OVocKPj/R3bE/O/IDlce2UFEVK9G2zU2e/ZsfPPNN/jiiy8QHx+P3377DdnZ2ZgxYwb++c9/Yvr06Q1OXkm4a6w6Ne3uUcoOjLT8UryzIQP7zlwFADR312PakLbwuXwcI0c0jdpSU11JGctdY9Jw15g88dw1dpuXX34ZZrMZw4YNQ2lpKQYPHgwXFxe8+OKLTW4R9FfcNVadmnb32HsHRq+2vvjhqRbYdDwf76xLx+mCErz1Wwb83HQwhF3FiK4B0Gg0Dc5bCdRUV1LGcteYNNw1Jk98U901ZvVCSKPR4NVXX8XMmTORmZmJ4uJihIeHw8PDw+okiUgcjUaD4Xf4I7ZzK3y39yzmb8pAfqkJf/82FX3bncWro8PRrY23vdMkInI4Vi+EvvnmG4wfPx4GgwHh4eGNkZMilZSUQKfT1XjdZDLhxo0bKCkpqfWRn5RrSmarvOWcR+q9rB0nNl5MXH0x93Rvidi27njtm2TsuuiEXem5uDM9F2MjAvBcXAe0dHdyuNpSU11JGStXbTXkuiP+zrJlznLN5Yh1ZSnGXnVVUlIiKs7qHqGWLVvi+vXrGDt2LB5++GGMGDGi1gVCU3GrR4iIiIgcj6UeIas/RygvLw/ff/89NBoN7r//frRu3RrPPPMMdu3a1aBElSYpKQnh4eHo06ePvVMhIiKiRtKgs8ZKS0uxcuVKLFu2DJs3b0abNm1w6tQpOfOzu1tPhLKzs+vcNbZ161YMHTq01kd+Uq4pma3ylnMeqfeydpzYeDFxlmJquy4IAlJOXsa8zRnIKrgOAAhp4YYZwzogtpNvrQ3VSqGmupIyVq7aash1R/ydZcuc5ZrLEevKUoy96spoNCIkJKRxzhq7xWAwYMSIEbh69Sqys7ORlpbWkNspmo+PT50LIVdXV/j4+NT6FyzlmpLZKm8555F6L2vHiY0XE2cppq7rd0U1w/DuQXj9qw3YetENOdduInFVBvqEXsKrd4YjMsjH8jduB2qqKylj5aqthlx3xN9ZtsxZrrkcsa4sxdirrrRacW96Wf3WGFD5JOjbb7/F6NGjERgYiAULFuDuu+/GsWPHpNyOiGTkpNNioL+AzTMGYvrQMLjqtdh35irGJe3E9O8OIedKqb1TJCJSDKufCD3wwAP49ddfYTAYcP/99+Of//wn+vXr1xi5EVEDeLg44YXhnTAxOhjvb8zATwfP4ZfDudhw9AIeGxCKZ2LC4G1wjP9nT0TUWKxeCOl0Ovzwww9NfrcYUVPR2tsNc++LwKQBoXj7tzTszLyMxSmn8cP+HDw7tAMe7hsCZydJD4eJiByeVb/9TCYTLly4gA4dOnARRORg7gjwxjeTo/HlpD7o0MoDhaUmvPXrccTP3451f+ahAfsmiIgcllVPhPR6PY4cOdJYuSiaycTT5wHb5S3nPFLvZe04sfFi4izFNKS2BrZrhjVP98VPh3KxYEsmsi+XYuq3B9Ez2Acvj+yIHnZoqFZTXUkZK1dtNWZdKZEtc5ZrLkesK0sx9qorsfe0evv8jBkz4OLignfeeUdSYo6Cp8+TGpRVAFtytdiWq8FNc+X2+sgWZowJNsPX1c7JERE1QKOdPj99+nQsXboUHTp0QK9eveDu7l7t+rx586RlrFA8fb46W+Ut5zxS72XtOLHxYuIsxchdW/nGG/hg6ymsOHgeggDodRo8HB2Mp4e0g48NGqrVVFdSxspVW7auK3uzZc5yzeWIdWUpxl511Winzx89ehQ9e/YEAGRkZFS7puQPbGsoSyfjKunEXVuwVd5yziP1XtaOExsvJq6x6u52bVroMee+SDw+sB1mr0tHSsYlfLkrGz8fysX0oWF4pF8IXJwavy9QTXUlZaxctWWrulIKW+Ys11yOWFeWYmxdV2LvZ/VCaNu2bVYnQ0SOoUtrLyx9PArbMy5h9m9pSL9wDf9em4avdp/BP0Z2xp3dWjfp/8NDROojec9sZmYmNmzYgOvXKz/KnztOiJqOIR1bYu2zg/DePd3RytMFOVeuY9qyQxj/yS7sP3PF3ukREcnG6oXQ5cuXMWzYMHTs2BGjR49GXl4eAGDy5Ml44YUXZE+QiOxDp9Xg/j5BSJ4ZgxlxHWFw1uHQ2ULcu2g3pn5zAGcKSuydIhFRg1m9EJoxYwb0ej3Onj1bbRfVhAkTsH79elmTIyL7Mzg74bm4Dkh+MQYPRgVBqwHWHb2AuHnbMWvNMVwpuWnvFImIJLN6IbRx40a8++67aNOmTbXXO3TogOzsbNkSIyJlaeXlitnju2P984MR26klys0Cluw6gyFztuHT7adww1Rh7xSJiKxm9UKopKSk1s/TuXLlClxcXGRJioiUq6OfJ76cFIVvJkejS2svXLtRjtnr0jHs/e1YnXoeZjP7BYnIcVi9EBo0aBCWLl1a9bVGo4HZbMZ7772H2NhYWZMjIuUa2MEXv04fiLn3RcDfyxXnC6/jue9TcffHO/HH6cv2To+ISBSrt8+/9957GDZsGPbv34+bN2/ipZdewrFjx3DlyhXs3LmzMXJUBB6xUUlNRyEo9ePqLV23dW3d1d0Pwzv74std2Vi8IwuHzxVhwuI9iO/SCjOHd0BbX3eL91BTXUkZyyM2pOERG/LE84iNWhQVFeGjjz7C4cOHUVxcjJ49e+KZZ55B69atrU5UqXjEBpH1jDeB9ee02J2vgRkaaDUCBvgJGNnGDA/H+gw+InJwjXbEhtrwiI3q1HQUglI/rt7SdSXU1smLxZizMQPbThQAADxcnPD3wW2R0C8Yrvqan1CtprqSMpZHbEjDIzbkiecRG7dZv349PDw8MHDgQACVT04+++wzhIeHIykpCc2aNZOetYLxiI3q1HQUglI/rt7SdXvWVnhgM3w5KRq7ThXg7d/ScPS8EXM3ncSyvTmYObIT7ooIhFZb8xOq1VRXUsbyiA1peMSGPPFN9YgNq5ulZ86cCaPRCAD4888/kZiYiNGjRyMrKwuJiYnW3o6ImrD+7X2x5pmBmD8hAgHersgtuoEZyw9jbNLv2H2KDdVEZH9WPxHKyspCeHg4AOCnn37CmDFj8Pbbb+PgwYMYPXq07AkSkWPTajW4u0cbjOraGl/szMLH207h6HkjHvxsD+K6tMLLozojpJmrvdMkIpWy+omQs7MzSktLAQCbN2/G8OHDAQDNmzevelJERHQ7V70OT8eEYfvMGDzaLwQ6rQab0y5ixIIdeOOX47jmOJuRiKgJsfqJ0MCBA5GYmIgBAwZg7969WL58OQAgIyOjxqdNExHdroWHC966qysS+ofinXXp2HQ8H8v2noOLTocrPqfx5JCwWhuqiYgag9VPhD766CM4OTlhxYoV+OSTTxAYGAgAWLduHUaOHCl7gkTUNLVv6YHPHu2N5U/2RbdAL5RVaDBvcyaGzk3GzwfP8ROqicgmrH4iFBwcjF9//bXG6/Pnz5clISJSl+h2LbDiyWj8++v12HLJHblFN5D4w2F8ufMMXr2zC/q2a2HvFImoCbN6IQQAFRUVWLlyJdLS0gAAXbp0wbhx4+DkJOl2RKRyWq0GvVsKeGniAHy99xw+3nYKf54vwgOL9yCuix9eGd0Z7Vt62DtNImqCrF65HDt2DGPGjEF+fj46deoEAHj33XfRsmVL/PLLL+jatavsSRKROtxqqL6/dxA+2HwSy/aexea0fCSfuIiHooPx7LAOaOHBw52JSD5W9wg98cQT6Nq1K86dO4eDBw/i4MGDyMnJQffu3fHkk082Ro5EpDK+Hi7417iu2PD8IMR1aYVys4CvdmcjZk4yFm0/hRumCnunSERNhNULodTUVMyePbvaJ0g3a9YM//nPf3Do0CFZkyMidQtr5YnPE/pg2RPRuCPAC9fKyvHOunQMe3871hzOBU8IIqKGsnoh1LFjR+Tn59d4/eLFiwgLC5MlKSKiv+of5otfpg3E3Psi4O/livOF1/Hsd4cw7uNd2H/mir3TIyIHJqpH6K8flDh79mw8++yzmDVrFvr27QsA2LNnD9566y28++67jZOlAphMJphMNT/x7dZrcl5TMlvlLec8Uu9l7Tix8WLiLMU0tdoSm/Nd3f0wvLMvvtiVjcU7snA4pxD3LtqNEeGtMHN4R4S0MMgyj5w5yzFWrtpiXSl/LkesK0sx9qorsfcUdfq8VquFRvP/D0i8NeTWa3/9uqKiabx3n5SUhKSkJFRUVCAjIwPLli2DwVD/L1kish3jTWBdjha7L2ogQAOdRsBAfwEjAs1wd6wzQYmoEZSWlmLixIkWT58XtRDavn276ImHDBkiOtYRGI1GeHt7o6CgoNYfpMlkwqZNmxAfH1/jpFup15TMVnnLOY/Ue1k7Tmy8mDhLMU2tthqSc0b+Nby7IQMpJysPcfVydcIzMe3wUHQwXJyqv/uvhLqSMlau2mJdKX8uR6wrSzH2qiuj0QhfX1+LCyFRb401tcWNFHq9vt6/pPquS72mZLbKW855pN7L2nFi48XENVbdKZWUnO9o0xxLJ/dFSsYlvP1bGtIvXMPs9Rn4du85vDyqM0Z19a/2RFvqPHLmLHWsXLXFulL+XI5YV5ZibF1XYu8n6RMQCwsL8d///rfqAxXvuOMOPP744/D29pZyOyKiBhvcsSUGhPlixYEczN2YgbNXSvH0twfRK6QZXr2zC3oGN7N8EyJSHat3je3fvx/t27fH/PnzceXKFVy5cgXz5s1D+/btcfDgwcbIkYhIFJ1Wgwl9gpH8YgyeG9YBbnodDmRfxfiPd2HasoPIuVpq7xSJSGGsfiI0Y8YMjB07Fp999lnVkRrl5eV44okn8PzzzyMlJUX2JImIrOHu4oQZ8R3xYFQw5m06gR8PnMOvR/Kw4dgFDGqlxcDrJrRwsLd3iKhxSHoi9I9//KPauWJOTk546aWXsH//flmTIyJqCH9vV7x3bwTWTh+EgWG+MFUI2JqnxbD5v+PLnVkwVZjtnSIR2ZnVCyEvLy+cPXu2xus5OTnw9PSUJSkiIjmFB3jh68lR+OyRHvB3E1B43YQ3fzmO4fNTsOHYBX5CNZGKWb0QmjBhAiZPnozly5cjJycHOTk5+P777/HEE0/gwQcfbIwciYgaTKPRIKZjS7wUUYG3xnaBr4czsgpK8NTXBzBh8R4cOVdo7xSJyA6s7hGaO3cuNBoNHn30UZSXlwOo3KI2depUvPPOO7InSEQkJ50GeLBPEMb3Csai5FP4bMdp7M26grEf7cS4yADMHNkZgT5u9k6TiGzE6idCzs7O+OCDD3D16lWkpqYiNTUVV65cwfz58+Hi4tIYORIRyc7DxQkvjuiEbS/GYHyPQADAqtRcxM5Nxrvr03HthuMcJUFE0lm9ELrFYDCgW7du6NatG4+eICKHFeDjhnkTIvHr9IHo2645bpab8UnyKcTMScbXe7JRzoZqoiZN8kKIiKgp6Rroje+m9MXnj/ZGu5buuFxyE/9cdRQjFqRgS1o+G6qJmiguhIiI/kej0SAu3A8bnh+Mt+66A83dnXHqUgkmf7UfD33+B46eL7J3ikQkMy6EiIhuo9dp8Wi/UCTPjMHfh7SHs5MWu05dxpiPfscLPxzGhaIb9k6RiGTChRARUR28XPV4eVRnbEkcgrERARAE4KeD5xAzdxsWbMnEjQp7Z0hEDcWFEBGRBUHNDfjwwR5Y9cwA9AlthhsmM5KST+Pfh3RYvv8cG6qJHBgXQkREIkUG+eCHp/ph0cM9EdLcgGsmDV5bfRx3fvg7kk9ctHd6RCQBF0JERFbQaDQY2bU1fpveH3eHVsDHTY8T+dfw2Jf78Mh//0D6BaO9UyQiK6hiIZSVlYXY2FiEh4ejW7duKCkpsXdKROTgnJ20iGktYPOMgZgyqC30Og12nCzA6A924B8rjuCikQ3VRI5AFQuhxx57DG+99RaOHz+O7du38xOwiUg23m56vHpnOLYkxuDO7q1hFoDl+3MQMzcZH2w+idKb5fZOkYjq0eQXQseOHYNer8egQYMAAM2bN4eTk9VHrBER1Su4hQFJE3vip6n90SPYB6U3KzB/cwZi5ybjh/05qDDzAxmJlMjuC6GUlBSMGTMGAQEB0Gg0WLVqVY2YpKQkhIaGwtXVFdHR0di7d6/o+588eRIeHh4YM2YMevbsibffflvG7ImIqusV0gw/T+2Pjyb2QFBzN+Qby/DSiiP428Lf8fvJAnunR0S3sfujkZKSEkRERODxxx/H+PHja1xfvnw5EhMTsWjRIkRHR2PBggUYMWIETpw4gVatWgEAIiMjUV5e8/Hzxo0bUV5ejh07diA1NRWtWrXCyJEj0adPH8THxzf690ZE6qTRaPC37gGID/fD0l3ZWLj1JNLyjHj4v38gtlNLzBzewd4pEtH/2H0hNGrUKIwaNarO6/PmzcOUKVMwadIkAMCiRYuwdu1afPHFF3j55ZcBAKmpqXWODwwMRO/evREUFAQAGD16NFJTU+tcCJWVlaGsrKzqa6OxcgeIyWSCyVTzNOpbr8l5Tclslbec80i9l7XjxMaLibMU09Rqq6nWlRbAY/2CcFeEH5KST+PbP3Kw7cQlpGQUoG8rLXpcLUHrZu6y5d2QurF0nXVlm7kach+l/s6yV12JvadGUNBJghqNBitXrsS4ceMAADdv3oTBYMCKFSuqXgOAhIQEFBYWYvXq1RbvWV5ejj59+mDr1q3w9vbGXXfdhaeeegp/+9vfao2fNWsW3nzzzRqvL1u2DAaDQdL3RUQEABevA7+c1eLIlcquBBedgLgAM2JaC3DW2Tk5oiamtLQUEydORFFREby8vOqMs/sTofoUFBSgoqICfn5+1V738/NDenq6qHs4OTnh7bffxuDBgyEIAoYPH17nIggAXnnlFSQmJlZ9bTQaERQUhOHDh9f6gzSZTNi0aRPi4+Oh1+tluaZktspbznmk3svacWLjxcRZimlqtaWmunoMwO7MS3htxUGcLdFgbY4OB4pc8EJ8B4zt3hparUbyXA2pG0vXWVe2mash91Hq7yx71dWtd3QsUfRCSC6W3n77KxcXl1q31+v1+nr/kuq7LvWaktkqbznnkXova8eJjRcT11h1p1Rqqat+YS0xo1sFzG16YN7mTJwvvI6ZPx3F0j05ePXOLujbrkWD5mpI3Vi6zrqyzVwNuY9Sf2fZuq7E3k/RCyFfX1/odDrk5+dXez0/Px/+/v42zYU9QpWaai+HHOPYIySdmurq1hitBhgR7osR4a2wZPdZLErJwp/ni/DA4j0Y1rklXhreEe1auls1F3uEqmOPkDzx7BGyodt7hAAgOjoaUVFRWLhwIQDAbDYjODgY06ZNq2qWbgxJSUlISkpCRUUFMjIy2CNERI2q2ASsy9FiV74GZmighYABfgJGBpnh4VgPYIgUQWyPkN0XQsXFxcjMzAQA9OjRA/PmzUNsbCyaN2+O4OBgLF++HAkJCfj0008RFRWFBQsW4IcffkB6enqN3qHGYDQa4e3tjYKCAvYIQV29HEp9v93SdUesLTXVlaWxpy6V4L0NGdh64hIAwMPFCU8NDEbr4gyMHsEeIWuwR0ieeEfuEfL19VV+s/T+/fsRGxtb9fWtRuWEhAQsWbIEEyZMwKVLl/D666/jwoULiIyMxPr1622yCPor9ghVp5ZeDinj2CMknZrqqq6xnQN88MWkKOw6VYD/rE3DsVwj3t9yGs1ddNAGF+DunkHQaGo2VFuTE+tK+XOxR6jhHKZHKCYmBpYeSk2bNg3Tpk2zUUa1Y49QJTX1cij1/XZL1x2xttRUV2LH9gn2xs9PRWP14Ty8v+kk8q+VIfHHP7FkdzZeGdkJvUOaWX1f1pXy52KPkHwcskdISdgjRERKcbMCSM7TYPN5LcrMlU+Dujc3Y2ywGS3d7JwckUI5TI+Q0rFHqDo19XIo9f12S9cdsbbUVFdSxt6Kj+w3GB+nnMWPB87BLAB6nQYPRQXhmZj28DHo2SN0G/YIyRPPHiECwB6h26mpl0Op77dbuu6ItaWmupIyNqCZB969NwKTB7XD27+lIfnEJSzZfRY/H8rFs8M64IHegaLuy7pS/lzsEWo4sfez++nzRERknY5+nlgyKQpfT45CZ39PGG+U499r0zDqw504dFljse+SiP4/PhESic3SldTU1KrUxkNL1x2xttRUV1LG1hXfN9QHq6b2xc+HcrFgSyZyrl7Hkqs6HF78B14Z3Rk9gnysmpd1Zf+5lFBXUuKU+G8hm6UbiM3SRORIyiqArblabM3V4Ob/Gqp7tDBjTLAZLVztnByRHbBZWiZslq5OTU2tSm08tHTdEWtLTXUlZaw1tbVi7SakVgRh5eE8CP9rqH60bzCeHtIObk5gXSl8LqXWFZulic3St1FTU6tSGw8tXXfE2lJTXUkZKybe2xl4d3Q3TBkShrd/S8OOkwX4785s/HQoF9Ni2qG5mXXlCHMpra7Exinp30I2SxMRqViX1l5Y+ngUvpzUBx1aeaCw1IR//3YCsw/rsOn4RTZUE/0PF0JERE2URqNBbKdWWPfcILx9dze0cHfGpRsaPP1dKiYs3oMj5wrtnSKR3fGtMZG4a6ySmnb3KHUHhqXrjlhbaqorKWPlqK37erZGfEcfvPrNdmzPd8LerCsY+9FOjO3eGi/EhyHAx411pYC5HK2uxMRw15iD4q4xImqqCsuAX3O02Hep8k0BJ42AmNYC4gPNcOX/PaYmgrvGZMJdY9WpaXePUndgWLruiLWlprqSMlau2rr9+rFcI2avP4E/sq4CAJob9BjqdwOvPzQUbi4usn2/9sJdY/LEc9cYAeCusdupaXePUndgWLruiLWlprqSMlau2rp1PTKkBb5/sh+2pF3E2+vScPpSCVZk6XBw0X68emcXDO3cChqNpkE5KwF3jckTz11jRETU5Gg0GsSF+2HD84Mx62+d4e4k4HRBCSZ/tR8Pff4HjuUW2TtFokbFJ0IilZSUQKfT1XjdZDLhxo0bKCkpqfWRn5RrSmarvOWcR+q9rB0nNl5MnKWYplZbaqorKWPlqi1L18d1bQFkl+CMazt888c5/J52HqPTz2NcZCCeHhLKurLBXI5YV5Zi7PX7qqSkRFQce4QsuNUjRERERI7HUo8Q3xqrQ1JSEsLDw9GnTx97p0JERESNhE+ELLj1RCg7O7vOXWNbt27F0KFDa33kJ+WaktkqbznnkXova8eJjRcTZymmqdWWmupKyli5akvqdUEQsOFYHt5dexyXyyqbpzu2ckdifEf0b99czLdsF7b834JcczliXVmKsdfvK6PRiJCQEO4ak4uPj0+dCyFXV1f4+PjU+hcs5ZqS2SpvOeeRei9rx4mNFxNnKaap1Zaa6krKWLlqqyHX74n2gP7SSVxufgeSkk8js9CEp39MQ0ynlvi/0V3Q0c9TxHduW7b834JcczliXVmKsdfvK61W3JtefGuMiIhEcdICk/qHYPvMGDw+oC30Og2ST1zCyAUp+L+Vf+LStTJ7p0hkNS6EiIjIKj4GZ7w+JhybZgzByDv8YRaAZX+cRcycbUjalokbpgp7p0gkGhdCREQkSaivOxY90gs/PNUPEW28UXKzAnM2nMDQuclYeegczGa2oJLycSFEREQNEtW2OVY+PQAfPBCJQB835BbdwIzlhzHu45344/Rle6dHVC82S4tkMvH0ecB2ecs5j9R7WTtObLyYOEsxTa221FRXUsbKVVuNXVej72iFoR1b4KvdZ/FJymkcOVeECYv3IL5LK8wc3gFtfd3rzV9utvzfglxzOWJdWYqx1+8rsffk9vk68PR5IiLprpmAdTla7M7XwAwNtBoBA/0EjGxjhrtjbGYkB8fT52XC0+ers1Xecs4j9V7WjhMbLybOUkxTqy011ZWUsXLVlj3qKvNiMd7dkIHkjAIAgJerE56OaYeHo4Ph4tS43Rm2/N+CXHM5Yl1ZirHX7yuePi8zSyfjKunEXVuwVd5yziP1XtaOExsvJq6x6k6p1FRXUsbKVVu2rKsugc2w5PFo7MwswL/XpiEtz4h31mfg2705eHlkF4zu5l/jhHu52fJ/C3LN5Yh1ZSnG1r+vxN6PzdJERNToBoT54tfpA/Hevd3RytMFOVeu45llB3Hvot04ePaqvdMjFeNCiIiIbEKn1eD+3kFInhmD5+M6wE2vw4Hsqxj/8S5MW3YQOVdK7Z0iqRAXQkREZFMGZyc8H9cRyTNjcH/vNtBogF+P5GHY+9sx+7c0FF13nB2P5Pi4ECIiIrvw83LFe/dGYO30QRgY5oubFWZ8mnIaMXO24atdZ2CqMNs7RVIBLoSIiMiuwgO88PXkKHz5WB+EtfLA1VIT3lhzDCMWpGDT8XxwczM1Ji6EiIjI7jQaDWI7t8L65wbh3+O6ooW7M05fKsGUpfvx4Gd7cPR8kb1TpCaKCyEiIlIMJ50WD/cNQfLMGDwd0x4uTlrsOX0FYz76HYk/pCKv6Lq9U6Qmhp8jJBKP2KikpqMQlPpx9ZauO2JtqamupIx1lCM25OSqA2YMa48JvQLw/qZMrDmSh58Pnsdvf+bh8f6hmDIoFB4u9f8TxiM25InnERsqxSM2iIiUI7sYWH1Gh1PXKj980VMvYHSQGdGtBOga9/MYyUHxiA2Z8IiN6tR0FIJSP67e0nVHrC011ZWUsY58xIacBEHAprSLeG/DSWT/7zOHOrbywMsjO2JQB98a8TxiQ554HrFBAHjExu3UdBSCUj+u3tJ1R6wtNdWVlLGOeMSG3O6MaIP4OwLwzZ5sfLj1JDIuFuPxpQcxuGNLvDq6Czr5e9YYwyM25InnERtEREQK4OykxeMD22L7i7F4YmBb6HUapGRcwqgPUvDKz0dw8doNe6dIDoQLISIickjeBj1e+1s4NicOwehu/jALwHd7cxAzJxkLt5zE9ZsV9k6RHAAXQkRE5NBCWrjj44d6YcXf+yEyyAelNyvw/qYMxH/wO/Ze0sBsZiss1Y0LISIiahJ6hzbHyqf748MHeyDQxw35xjJ8m6nD+E/3YPepy/ZOjxSKCyEiImoyNBoNxkYEYMsLQzBzeAe46gQcy72GBz/bgye+2odTl4rtnSIpDHeNERFRk+Oq1+HJQW3hcyUNabq2+G7fOWxOu4jkE5fwUHQwnovriObuzvZOkxSAT4SIiKjJ8tADb/ytCzY8PxhxXVqh3Czgq93ZGDJnGz7dfgo3TGyoVjsuhIiIqMkLa+WBzxP6YNmUaNwR4IVrN8oxe1064uZtx5rDuTzhXsW4ECIiItXo394Xv0wbiLn3RcDfyxXnrl7Hs98dwvhPduFA9hV7p0d2wIUQERGpilarwb292mDbizFIjO8Ig7MOh84W4p5PduOZbw8i+3KJvVMkG+JCiIiIVMnNWYdnh3VA8osxeKBPELQaYO2feYibtx3//vU4ikob/9R6sj/uGhPJZDLBZKr5P4pbr8l5Tclslbec80i9l7XjxMaLibMU09RqS011JWWsXLXFuqpdMzcd/jW2Cx6OaoN3NmTg98zL+Pz3LKw4cA7PxLbDxD5BcHaq/7mBXD8fR6wrSzH2qiux9+Tp83VISkpCUlISKioqkJGRgWXLlsFgMNg7LSIiamRpVzVYla3FhesaAEBLVwFjgs3o3lyARmPn5Ei00tJSTJw40eLp81wIWWA0GuHt7Y2CgoJaf5AmkwmbNm1CfHx8jZNupV5TMlvlLec8Uu9l7Tix8WLiLMU0tdpSU11JGStXbbGuxCuvMGPFwVws2JKJyyU3AQB9QpvhlZEd0S3QW9a55LqPUn9n2auujEYjfH19LS6E+NaYSHq9vt6/pPquS72mZLbKW855pN7L2nFi48XENVbdKZWa6krKWLlqi3UlZgzwSP+2uLtXEBYln8JnO05j35mrGL/oD4yLDMDMkZ0R6OMmy1xy5Sx1rK1+Z9m6rsTej83SREREdfBwccKLIzoheWYMxvcMBACsSs3F0LnJeG99Oq7dcJyeKaodF0JEREQWtPZ2w7z7I/HLtIGIbtscZeVmfJx8CrFzk/HNnmyUV5jtnSJJxIUQERGRSN3aeOP7J/ti8SO90M7XHQXFN/HaqqMYk7Qbx65q+AnVDogLISIiIitoNBoMv8MfG2YMxptj70Azgx6Zl0qwOF2Hx746gLQ8o71TJCtwIURERCSBXqdFQv9QJM+MxeQBIdBpBOw6dQWjP9yBf6w4gnzjDXunSCJwIURERNQA3m56vDyyE16NrMCdXf0hCMDy/TmImZOMBZszUHqz3N4pUj24ECIiIpJBC1dgwYTu+Pnp/ugZ7IPrpgos2HwSsXOT8cP+HFSY2T+kRFwIERERyahncDP8NLU/kib2RFBzN+Qby/DSiiMYs/B37MwssHd6dBsuhIiIiGSm0WhwZ/fW2Jw4BK+O7gJPVycczzPioc//wONL9iHz4jV7p0j/w4UQERFRI3Fx0mHK4HZImRmLx/qHwkmrwdb0ixixYAdeW/UnCorL7J2i6nEhRERE1MiauTtj1tg7sHHGYAwP90OFWcA3e84iZk4yPk7OxA1Thb1TVC0uhIiIiGykXUsPLH60N75/si+6BXqjuKwc760/gWHvb8fq1PMws6Ha5njoKhERkY31bdcCq58ZgNWHz+O99SdwvvA6nvs+Fd0DvRDjY+/s1IVPhIiIiOxAq9Xg7h5tsO3FGMwc0QnuzjocOW/Eh8ec8Mx3qThTUGLvFFWBCyEiIiI7ctXr8ExsGJJnxuKBPm2ggYCNxy8ifv52vPXLcRSW3rR3ik0aF0JEREQK0NLTBf8aG45/RFRgSAdfmCoEfLEzC0PmJOPzHadxs5wn3DeGJr8QOnHiBCIjI6v+uLm5YdWqVfZOi4iIqFatDcDnj/bE15Oj0NnfE0XXTfj32jTEz9+OdX/m8YR7mTX5ZulOnTohNTUVAFBcXIzQ0FDEx8fbNykiIiILBnVoibXP+mLFgRzM3ZiB7MulmPrtQfQJbYZX7wxHZJCPvVNsEpr8E6G/WrNmDYYNGwZ3d3d7p0JERGSRTqvBhD7BSH4xBs8O6wBXvRb7zlzFuKSdePa7Qzh3tdTeKTo8uy+EUlJSMGbMGAQEBECj0dT6tlVSUhJCQ0Ph6uqK6Oho7N27V9JcP/zwAyZMmNDAjImIiGzL3cUJifEdkfxiLO7t1QYaDbDmcC6Gvr8d76xLh/GGyd4pOiy7L4RKSkoQERGBpKSkWq8vX74ciYmJeOONN3Dw4EFERERgxIgRuHjxYlVMZGQkunbtWuNPbm5uVYzRaMSuXbswevToRv+eiIiIGoO/tyvm3heBX6YNRP/2LXCz3IxF208hZk4yvv3jLCrYPmQ1u/cIjRo1CqNGjarz+rx58zBlyhRMmjQJALBo0SKsXbsWX3zxBV5++WUAqOoBqs/q1asxfPhwuLq61htXVlaGsrL/f/aL0WgEAJhMJphMNVfct16T85qS2SpvOeeRei9rx4mNFxNnKaap1Zaa6krKWLlqi3Wl/LnE3qdTKwOWJPTEtowCvLs+A6cLSjDr13T4uengGpqHuHB/aDQaWeZq6O8se9WV2HtqBAW1n2s0GqxcuRLjxo0DANy8eRMGgwErVqyoeg0AEhISUFhYiNWrV4u+95gxY/Dkk09izJgx9cbNmjULb775Zo3Xly1bBoPBIHo+IiIiW6gwA7suarAuR4uS8srFTwcvM8aFmtFGxS2xpaWlmDhxIoqKiuDl5VVnnN2fCNWnoKAAFRUV8PPzq/a6n58f0tPTRd+nqKgIe/fuxU8//WQx9pVXXkFiYmLV10ajEUFBQRg+fHitP0iTyYRNmzYhPj4eer1elmtKZqu85ZxH6r2sHSc2XkycpZimVltqqispY+WqLdaV8ueSep8xAGZeu47/+2Y7duQ74aQRmPunFndHBmBGXBj8vWq+G2Kr31n2qqtb7+hYouiFkFy8vb2Rn58vKtbFxQUuLi41Xtfr9fX+JdV3Xeo1JbNV3nLOI/Ve1o4TGy8mrrHqTqnUVFdSxspVW6wr5c8l5T7NPYGxIWa89sAAzN9yCmsO5+LnQ7lYdzQfUwa3w1OD28HdpeY/+7b6nWXruhJ7P0UvhHx9faHT6WosYvLz8+Hv72/TXNgjVElNvRzsEbIdNdWVlLHsEZKmKfcI1TfWz8MJ79/bFY9Et8E76zNw4GwhPtxyEt/vPYvnh7XH+B6B0Gk17BH6H0X3CAFAdHQ0oqKisHDhQgCA2WxGcHAwpk2bVtUs3RiSkpKQlJSEiooKZGRksEeIiIgcjiAAh69o8Eu2FgVllf1DAQYBd4WY0dlHMf/8NwqxPUJ2XwgVFxcjMzMTANCjRw/MmzcPsbGxaN68OYKDg7F8+XIkJCTg008/RVRUFBYsWIAffvgB6enpNXqHGoPRaIS3tzcKCgrYIwR19XKwR8h21FRXUsayR0gaNfUIWRpbVm7Gsr05SEo+haLr5QCAQWHNMcD9Ih69q+n2CPn6+iq/WXr//v2IjY2t+vpWo3JCQgKWLFmCCRMm4NKlS3j99ddx4cIFREZGYv369TZZBP0Ve4SqU1MvB3uEbEdNdSVlLHuEpFFLj1B9Y/V64MkhYbi/TzA+3JKJr/ecwY7MK/gdOpxxPokXhndGS8+a/bHW5qSkfwsdpkcoJibG4gFy06ZNw7Rp02yUUe3YI1RJTb0c7BGyHTXVlZSx7BGSRq09QvWNdddr8MrIDpjYJxDvrj+BTemX8P2+c/jlcB6eGtwWk/qHwFWvs/q+Svy30CF7hJSEPUJERNTUnTICq87ocLaksn/Ix1nA34LN6OUrQFv/5zEqnsP0CCkde4SqU1MvB3uEbEdNdSVlLHuEpGGPkLj4YXFx2JB2Ge9vOoncohsAgG6BXnh5ZEdEhTZnjxBVYo9QdWrq5WCPkO2oqa6kjGWPkDTsEaqfi7Mz7ukdjDsjAvHFzix8vO0U/jxvxEP/3Y/h4X54MT5M9H2V9G+h2PvZ/dBVIiIisj9XvQ5Px4QheWYMHu4bDJ1Wg43H8zF64S78lKXF1dKb9k6xUfCJkEhslq6kpqZWNkvbjprqSspYNktLw2ZpafHeLlq8cWdnPNSnDd7dkIHkjAKkXNAibv7veDqmHR6ODoaLk1bUvRpyraHYLN1AbJYmIiICThRpsPqMFudLK7unW7gIGBNiRmRzARYOuLcrNkvLhM3S1ampqZXN0rajprqSMpbN0tKwWVqeeJPJhA0bN6GkVVd8uC0LF6+VAQB6Bvvg5ZEd0SPIR5H/FrJZWmZslq5OTU2tbJa2HTXVlZSxbJaWhs3SDY/XaoAJfYIxvncIFqecxqfbT+Pg2ULcv3gv/ta9NRLj2lu8F5uliYiIyKEZnJ3wfFxHJM+Mwf2920CjAX49kocRH+zE6mwtjNcdp4fsFi6EiIiIyCp+Xq54794IrJ0+CAPDfGGqELA1V4u4Bb/jq11nYKow2ztF0fjWmEjcNVZJTbt7uGvMdtRUV1LGcteYNNw1Jk98fXEdWrrhi0d7YEtaPmatOoz8UhPeWHMMX+3KwkvDO2Jo55YoLy+vczx3jSkYd40RERGJVyEAu/M1WJejRXF55XayMC8zxoWYEeRh+3y4a0wm3DVWnZp293DXmO2oqa6kjOWuMWm4a0yeeGt/Z92o0GDxjix8uSsbZeVmaAD0bmnGuw8NQFALT9m+X0u4a0xm3DVWnZp293DXmO2oqa6kjOWuMWm4a0yeeLG/swwGPV4eHY5H+rfFnPXpWJWai32XtBid9AemDGqHp4a0h4eLU41x3DVGRERETUagjxsWPNADPz0VjfaeAm6YzFi4NRMxc5Lx3d6zKFdIQzWfCIlUUlICnU5X43WTyYQbN26gpKSk1kfJUq4pma3ylnMeqfeydpzYeDFxlmKaWm2pqa6kjJWrtlhXyp/LEevKUkz7Zk6Y0r4E+tAeWLAlE9mXi/CP7/fh861pSIwLa7S/o5KSElFx7BGy4FaPEBERETkeSz1CfGusDklJSQgPD0efPn3snQoRERE1Ej4RsuDWE6Hs7Ow6d41t3boVQ4cOrfVRspRrSmarvOWcR+q9rB0nNl5MnKWYplZbaqorKWPlqi3WlfLncsS6shRT37XTF4346Jc/8M4jQ+Ds7CziuxTPaDQiJCSEu8bk4uPjU+dCyNXVFT4+PrX+5Uu5pmS2ylvOeaTey9pxYuPFxFmKaWq1paa6kjJWrtpiXSl/LkesK0sx9V3r5u6Ou8Kc0axZM9n/jrRacW968a0xIiIiUi0uhIiIiEi1uBAiIiIi1eJCiIiIiFSLzdIimUw8fR6wXd5yziP1XtaOExsvJs5STFOrLTXVlZSxctUW60r5czliXVmKsVddib0nt8/XgafPExEROS6ePi8Tnj5fna3ylnMeqfeydpzYeDFxlmKaWm2pqa6kjJWrtlhXyp/LEevKUoy96oqnz8vM0sm49V2Xek3JbJW3nPNIvZe148TGi4lrrLpTKjXVlZSxctUW60r5czliXVmKsXVdib0fm6WJiIhItbgQIiIiItXiQoiIiIhUiwshIiIiUi0uhIiIiEi1uGvMglufLmA0Gmu9bjKZUFpaCqPRWOu2QCnXlMxWecs5j9R7WTtObLyYOEsxTa221FRXUsbKVVusK+XP5Yh1ZSnGXnV1699tS58SxIWQBdeuXQMABAUF2TkTIiIista1a9fg7e1d53V+oKIFZrMZubm58PT0hEajqTWmT58+2Ldvn1XXjEYjgoKCkJOTU+8HPSlRfd+vUueRei9rx4mNFxNnKaap1Zaa6krKWLlqi3Wl/Lkcsa4sxdijrgRBwLVr1xAQEACttu5OID4RskCr1aJNmzb1xuh0ujr/Auu7BgBeXl4O9UsFsPw9KXEeqfeydpzYeDFxlmKaWm2pqa6kjJWrtlhXyp/LEevKUoy96qq+J0G3sFlaBs8884yka47KVt+TnPNIvZe148TGi4mzFNPUaktNdSVlrFy1xbpS/lyOWFeWYpRcV3xrzE5unWFm6QwUImuxtqgxsK6oMSihrvhEyE5cXFzwxhtvwMXFxd6pUBPD2qLGwLqixqCEuuITISIiIlItPhEiIiIi1eJCiIiIiFSLCyEiIiJSLS6EiIiISLW4ECIiIiLV4kLIARQWFqJ3796IjIxE165d8dlnn9k7JWoCcnJyEBMTg/DwcHTv3h0//vijvVOiJuLuu+9Gs2bNcO+999o7FXJwv/76Kzp16oQOHTrg888/b5Q5uH3eAVRUVKCsrAwGgwElJSXo2rUr9u/fjxYtWtg7NXJgeXl5yM/PR2RkJC5cuIBevXohIyMD7u7u9k6NHFxycjKuXbuGr776CitWrLB3OuSgysvLER4ejm3btsHb2xu9evXCrl27ZP+3j0+EHIBOp4PBYAAAlJWVQRAEcP1KDdW6dWtERkYCAPz9/eHr64srV67YNylqEmJiYuDp6WnvNMjB7d27F3fccQcCAwPh4eGBUaNGYePGjbLPw4WQDFJSUjBmzBgEBARAo9Fg1apVNWKSkpIQGhoKV1dXREdHY+/evVbNUVhYiIiICLRp0wYzZ86Er6+vTNmTUtmirm45cOAAKioqEBQU1MCsSelsWVekbg2ttdzcXAQGBlZ9HRgYiPPnz8ueJxdCMigpKUFERASSkpJqvb58+XIkJibijTfewMGDBxEREYERI0bg4sWLVTG3+n9u/5ObmwsA8PHxweHDh5GVlYVly5YhPz/fJt8b2Y8t6goArly5gkcffRSLFy9u9O+J7M9WdUUkR63ZhECyAiCsXLmy2mtRUVHCM888U/V1RUWFEBAQIMyePVvSHFOnThV+/PHHhqRJDqax6urGjRvCoEGDhKVLl8qVKjmQxvx9tW3bNuGee+6RI01qAqTU2s6dO4Vx48ZVXX/uueeEb7/9Vvbc+ESokd28eRMHDhxAXFxc1WtarRZxcXHYvXu3qHvk5+fj2rVrAICioiKkpKSgU6dOjZIvOQY56koQBDz22GMYOnQoHnnkkcZKlRyIHHVFJIaYWouKisLRo0dx/vx5FBcXY926dRgxYoTsuTjJfkeqpqCgABUVFfDz86v2up+fH9LT00XdIzs7G08++WRVk/T06dPRrVu3xkiXHIQcdbVz504sX74c3bt3r3rv/uuvv2ZtqZgcdQUAcXFxOHz4MEpKStCmTRv8+OOP6Nevn9zpkgMTU2tOTk54//33ERsbC7PZjJdeeqlRdktzIeQAoqKikJqaau80qIkZOHAgzGazvdOgJmjz5s32ToGaiLFjx2Ls2LGNOgffGmtkvr6+0Ol0NZqb8/Pz4e/vb6esyNGxrqgxsK7IVpRUa1wINTJnZ2f06tULW7ZsqXrNbDZjy5YtfFRMkrGuqDGwrshWlFRrfGtMBsXFxcjMzKz6OisrC6mpqWjevDmCg4ORmJiIhIQE9O7dG1FRUViwYAFKSkowadIkO2ZNSse6osbAuiJbcZhak30fmgpt27ZNAFDjT0JCQlXMwoULheDgYMHZ2VmIiooS9uzZY7+EySGwrqgxsK7IVhyl1njWGBEREakWe4SIiIhItbgQIiIiItXiQoiIiIhUiwshIiIiUi0uhIiIiEi1uBAiIiIi1eJCiIiIiFSLCyEiIiJSLS6EiKhKcnIyNBoNCgsL7Z0Kdu7ciW7dukGv12PcuHH2ToeImiguhIgU4LHHHoNGo6nx56/n9MgtJiYGzz//fLXX+vfvj7y8PHh7ezfavGIlJiYiMjISWVlZWLJkSaPNM2vWLERGRjbKvWv7GdcmNDQUCxYsaJQcNBoNVq1a1Sj3JmoKuBAiUoiRI0ciLy+v2p+2bdvWiLt582aj5eDs7Ax/f39oNJpGm0OsU6dOYejQoWjTpg18fHzsnQ41EpPJZO8USO1sfroZEdWQkJAg3HXXXbVeGzJkiPDMM88Izz33nNCiRQshJiZGEARBeP/994WuXbsKBoNBaNOmjTB16lTh2rVr1cb+/vvvwpAhQwQ3NzfBx8dHGD58uHDlyhUhISGhxkGIWVlZVYckXr16teoeK1asEMLDwwVnZ2chJCREmDt3brU5QkJChP/85z/CpEmTBA8PDyEoKEj49NNP6/1+b9y4IUyfPl1o2bKl4OLiIgwYMEDYu3evIAiCkJWVVSO3L7/8stb7hISECG+99ZbwwAMPCAaDQQgICBA++uijajHZ2dnC2LFjBXd3d8HT01O47777hAsXLgiCIAhffvllnXNdvXpVmDx5suDr6yt4enoKsbGxQmpqatV933jjDSEiIkJYunSpEBISInh5eQkTJkwQjEajIAhCnT/j2v5+b48TBEEoKCgQHnjgASEgIEBwc3MTunbtKixbtqzG9z9//vxqr0VERAhvvPFG1fW/3jckJKQq7uOPPxbatWsn6PV6oWPHjsLSpUur3QeAsGjRIuHOO+8U3NzchM6dOwu7du0STp48KQwZMkQwGAxCv379hMzMzGrjVq1aJfTo0UNwcXER2rZtK8yaNUswmUzV7vvxxx8LY8aMEQwGQ1WuRPbChRCRAlhaCHl4eAgzZ84U0tPThfT0dEEQBGH+/PnC1q1bhaysLGHLli1Cp06dhKlTp1aNO3TokODi4iJMnTpVSE1NFY4ePSosXLhQuHTpklBYWCj069dPmDJlipCXlyfk5eUJ5eXlNRZC+/fvF7RarfDWW28JJ06cEL788kvBzc2t2sIkJCREaN68uZCUlCScPHlSmD17tqDVaqvyrM2zzz4rBAQECL/99ptw7NgxISEhQWjWrJlw+fJloby8XMjLyxO8vLyEBQsWCHl5eUJpaWmt9wkJCRE8PT2F2bNnCydOnBA+/PBDQafTCRs3bhQEQRAqKiqEyMhIYeDAgcL+/fuFPXv2CL169RKGDBkiCIIglJaWCi+88IJwxx13VP0cbs0VFxcnjBkzRti3b5+QkZEhvPDCC0KLFi2Ey5cvC4JQuRDy8PAQxo8fL/z5559CSkqK4O/vL/zf//2fIAhCnT/j212+fFlo06aN8NZbb1XFCYIgnDt3TpgzZ45w6NAh4dSpU1Xf2x9//FHt+69vIXTx4sWqxV1eXp5w8eJFQRAE4eeffxb0er2QlJQknDhxQnj//fcFnU4nbN26teo+AITAwEBh+fLlwokTJ4Rx48YJoaGhwtChQ4X169cLx48fF/r27SuMHDmyakxKSorg5eUlLFmyRDh16pSwceNGITQ0VJg1a1a1+7Zq1Ur44osvhFOnTgnZ2dl11gmRLXAhRKQACQkJgk6nE9zd3av+3HvvvYIgVC6EevToYfEeP/74o9CiRYuqrx988EFhwIABdcYPGTJEeO6556q9dvtCaOLEiUJ8fHy1mJkzZwrh4eFVX4eEhAgPP/xw1ddms1lo1aqV8Mknn9Q6b3FxsaDX64Vvv/226rWbN28KAQEBwnvvvVf1mre3d51Pgv4691//IRYEQZgwYYIwatQoQRAEYePGjYJOpxPOnj1bdf3YsWMCgKonULee7PzVjh07BC8vL+HGjRvVXm/fvn3V06433nhDMBgMVU+ABKHyZxMdHV31dW0/47q+j9sXNLW58847hRdeeKHecX9dCAlC5cJj5cqV1WL69+8vTJkypdpr9913nzB69Ohq41577bWqr3fv3i0AEP773/9Wvfbdd98Jrq6uVV8PGzZMePvtt6vd9+uvvxZat25d7b7PP/+8xe+VyFbYI0SkELGxsUhNTa368+GHH1Zd69WrV434zZs3Y9iwYQgMDISnpyceeeQRXL58GaWlpQCA1NRUDBs2rEE5paWlYcCAAdVeGzBgAE6ePImKioqq17p371713zUaDfz9/XHx4sVa73nq1CmYTKZq99Xr9YiKikJaWprVOfbr16/G17fuk5aWhqCgIAQFBVVdDw8Ph4+PT71zHT58GMXFxWjRogU8PDyq/mRlZeHUqVNVcaGhofD09Kz6unXr1nV+39aqqKjAv/71L3Tr1g3NmzeHh4cHNmzYgLNnzzb43nX9vd7+M/nr36ufnx8AoFu3btVeu3HjBoxGI4DKn9tbb71V7Wc2ZcoU5OXlVdUlAPTu3bvB3wORXJzsnQARVXJ3d0dYWFid1/7qzJkz+Nvf/oapU6fiP//5D5o3b47ff/8dkydPxs2bN2EwGODm5maLtAFULmT+SqPRwGw222x+uRUXF6N169ZITk6uce2vjduN+X3PmTMHH3zwARYsWIBu3brB3d0dzz//fLVmea1WC0EQqo2Ts/n4r9/frQb62l679T0XFxfjzTffxPjx42vcy9XVteq/317PRPbEJ0JEDujAgQMwm814//330bdvX3Ts2BG5ubnVYrp3744tW7bUeQ9nZ+dqT3Vq06VLF+zcubPaazt37kTHjh2h0+kk5d6+fXs4OztXu6/JZMK+ffsQHh5u9f327NlT4+suXboAqMw/JycHOTk5VdePHz+OwsLCqrlq+zn07NkTFy5cgJOTE8LCwqr98fX1FZ2bmJ9xXXE7d+7EXXfdhYcffhgRERFo164dMjIyqsW0bNkSeXl5VV8bjUZkZWVVi9Hr9TXuXdffq5Sf/1/17NkTJ06cqPEzCwsLg1bLf25ImViZRA4oLCwMJpMJCxcuxOnTp/H1119j0aJF1WJeeeUV7Nu3D08//TSOHDmC9PR0fPLJJygoKABQ+bbOH3/8gTNnzqCgoKDWJxkvvPACtmzZgn/961/IyMjAV199hY8++ggvvvii5Nzd3d0xdepUzJw5E+vXr8fx48cxZcoUlJaWYvLkyVbfb+fOnXjvvfeQkZGBpKQk/Pjjj3juuecAAHFxcejWrRseeughHDx4EHv37sWjjz6KIUOGVL09ExoaiqysLKSmpqKgoABlZWWIi4tDv379MG7cOGzcuBFnzpzBrl278Oqrr2L//v2icxPzM74Vl5KSgvPnz1f9/XTo0AGbNm3Crl27kJaWhqeeegr5+fnVxg0dOhRff/01duzYgT///BMJCQk1FqihoaHYsmULLly4gKtXrwIAZs6ciSVLluCTTz7ByZMnMW/ePPz8888N+nsFgNdffx1Lly7Fm2++iWPHjiEtLQ3ff/89XnvttQbdl6hR2btJiYgs7xqrreF23rx5QuvWrQU3NzdhxIgRwtKlS2tsfU9OThb69+8vuLi4CD4+PsKIESOqrp84cULo27ev4ObmJmr7vF6vF4KDg4U5c+ZUy0NMw+7trl+/LkyfPl3w9fWtsX3+FrHN0m+++aZw3333CQaDQfD39xc++OCDajH1bZ8XhMqt/Pfcc4/g4+NTbfu80WgUpk+fLgQEBAh6vV4ICgoSHnrooarG69qarOfPn19ti3ptP+Pa7N69W+jevbvg4uJStX3+8uXLwl133SV4eHgIrVq1El577TXh0UcfrVYnRUVFwoQJEwQvLy8hKChIWLJkSY2f/Zo1a4SwsDDBycnJ6u3zf22yvvWxBocOHap6rbZ6Wb9+vdC/f3/Bzc1N8PLyEqKiooTFixfXeV8ie9MIwm1vMBMROYjQ0FA8//zzoj69mYioNnxrjIiIiFSLCyEiIiJSLb41RkRERKrFJ0JERESkWlwIERERkWpxIURERESqxYUQERERqRYXQkRERKRaXAgRERGRanEhRERERKrFhRARERGpFhdCREREpFr/Dxr2BvTOeNcFAAAAAElFTkSuQmCC"]},"metadata":{}}],"source":["from scipy.special import logit, expit\n","print('K_i for tautomer 1 (in Molar):', true_taut1_kd)\n","print('K_i for tautomer 2 (in Molar):', true_taut2_kd)\n","\n","kiqs = []\n","xs = []\n","for x in np.linspace(0, 1, 1000):\n"," y = 1-x\n"," keq = x*(1/true_taut1_kd) + y*(1/true_taut2_kd)\n"," kiq = 1/keq\n"," kiqs.append(kiq)\n"," xs.append(x)\n","\n","plt.plot(xs, kiqs)\n","plt.yscale('log',)\n","plt.axhline(50/1e9, c='k')\n","plt.axhline(50/1e8, c='k')\n","plt.axhline(50/1e7, c='k')\n","plt.axhline(50/1e6, c='k')\n","plt.grid(which='both')\n","plt.xlabel('Fraction of potent tautomer')\n","plt.ylabel('observed Kd')\n","plt.title('')\n","plt.xscale('log')"],"metadata":{}}],"metadata":{"kernelspec":{"name":"python3","display_name":"Python 3 (ipykernel)","language":"python"},"language_info":{"name":"python","codemirror_mode":{"name":"ipython","version":3},"file_extension":".py","mimetype":"text/x-python","pygments_lexer":"ipython3"}},"nbformat":4,"nbformat_minor":5} |
Sign up for free
to join this conversation on GitHub.
Already have an account?
Sign in to comment