#SSA

Definição

SSA - É uma propriedade de IR, em que cada variavel é atribuida apenas uma vez, pro exemplo: y := 1 y := 2 x := y Será representada como: y1 := 1 y2 := 2 x1 := y2

Alguns algoritmos que são abilitados ou fortemente melhorados com SSA são:

• Constant Propagation
• Value Range Propagation
• Sparse Conditional
• Dead-code elimination
• Global value numbering
• Partial-redundancy elimination
• Strength reduction
• Register Allocation

Convertendo para SSA:

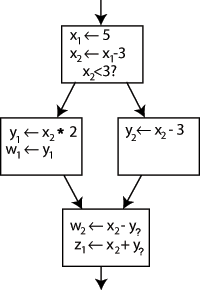
Suponha esse Control Flow Graph (CFG):

Pode ser explorado no SSA mudando x para as variaveis x1 e x2:

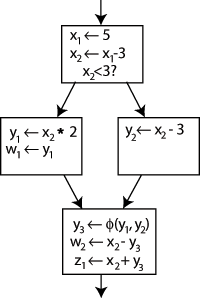
Note que no ultimo bloco não é possivel saber qual y vai ser ultilizado, para isso usamos uma phi-function (Φ-function), que diz qual variavel foi ultilizada, note que x2 não precisou de phi, pois Φ(x2,x2) = x2:

Em uma CFG arbritaria pode ser dificil dizer onde usar phi-function, mas esse problema pode ser facilmente resolvido usando um conceito chamado Dominance Frontiers.

Dominance and Dominance Frontiers

É dito que A domina estritamente B se para chegar em B temos que passar por A no grafo. A domina B se estritamente domina ou se A=B.

Se B é dominado por A e existe uma aresta de B->C onde C não é estritamente dominado por A, então C está na Dominance Frontier de A.

Ex:

For example, in this graph node 5’s dominated region
is shown in grey, and the border of that region is crossed
by edges 6 → 4, 8 → 5, 8 → 13, and 7 → 12. So we
say that nodes 4, 5, 12, 13 form the dominance frontier of
node 5.