Modified from:
2014-10-22 Justin Zhao, ADI Adapted from Zack Newman adicu.com http://www.columbia.edu/~jxz2101/#1
He who asks is a fool for five minutes, but he who does not ask remains a fool forever. .right[Chinese Proverb]
-
Review of Big O
-
Data Structures
-
Sorting Algorithms
-
Sample Interview Questions
-
"Big O" is the "asymptotic runtime"
-
Expressed as function of the size of the inputs
-
Consider best, worst, and average cases
/**
* Return the index of the minimum element in an integer array.
*/
public static int findMin(int[] array) {
int minIndex = 0;
for (int i = 0; i < array.length; i++) {
if (array[i] < array[minIndex]) {
minIndex = i;
}
}
}
/**
* Return the index of the minimum element in an integer array.
*/
public static int findMin(int[] array) {
int minIndex = 0; // O(1)
for (int i = 0; i < array.length; i++) { // n times
if (array[i] < array[minIndex]) { // O(1)
minIndex = i; // O(1)
}
}
} // O(1) + n (O(1) + O(1)) = O(1) + n O(1) = O(1) + O(n) = O(n)
/**
* Return the index of array (which must be sorted) at which value can be
* found, or -1 if it is absent.
*/
public static int find(int[] array, int value) {
return findHelper(array, 0, array.length - 1, value);
} // O(lg n)
private static int findHelper(int[] array, int minIndex, int maxIndex,
int value) {
if (maxIndex < minIndex) {
return -1;
}
int index = (maxIndex + minIndex) / 2;
if (value < array[index]) {
return findHelper(array, minIndex, index, value);
} else if (value > array[index]) {
return findHelper(array, index + 1, maxIndex, value);
} else {
return index;
}
}
Which performance is better?
O(10000 n) vs. O(n)
O(log n) vs. O(log(log n))
O(n log n) vs. O(n log k)
O(0.000001 n^2) vs. O(9999999 n^1.999999)
O(2^n) vs. O(3^n)
O(n!) vs. O(n^n)
-
What is a "data structure" anyway? We define ADTs first
-
An interface for interacting with data
-
lists, stacks, sets, queues, maps, trees, priority queue etc.
-
Defines operations and results, but not how they're implemented
-
Data Structure is an implementation of ADT
-
For example, an "ArrayList" or "HashMap"
-
Many ADTs can be implemented as the same Data Structure.
int[] array = {1, 3, 5, 2, 6, 9};
/*
* Index: 0 1 2 3 4 5
* Value: 1 3 5 2 6 9
*/
// Attributes
public class Node {
public int value;
public Node next;
public Node(int value, Node next) {
this.value = value;
this.next = next;
}
}
// Methods
public interface MyList {
public int get(int index);
public void update(int index, int value);
public void append(int value);
public String toString();
}
| Array | List | |
| Access | O(1) | O(n) |
| Update | O(1) | O(n) |
| Append | O(1)/O(n) | O(1) |
| Traversal | O(n) | O(n) |
Always think about the performance of the data structure
How about an "arraylist"?
import java.util.LinkedList;
import java.util.ArrayList;
import java.util.List;
// ...
List<Integer> a = new ArrayList<Integer>(){{
this.add(3);//inline adding.
}};
List<Integer> b = new LinkedList<Integer>();
for (int i = 0; i < 10; i++) {
a.add(i);
b.add(i);
}
a.set(5, 0);
b.remove(5);
System.out.println(a); // [0, 1, 2, 3, 4, 0, 6, 7, 8, 9]
System.out.println(b); // [0, 1, 2, 3, 4, 6, 7, 8, 9]
//iterate over linkedlist
for(int i=0; i<a.size()l; i++){
int item = a.get(i);
}
How do you reverse a linked list?
public static Node reverse(Node head) {
Node prev = null;
Node curr = head;
Node next;
while (curr != null ) {
next = curr.next;
curr.next = prev;
prev = curr;
curr = next;
}
return prev;
}
// Last-in first-out data structure
public interface MyStack {
// Add a value to the stack
public void push(int value);
// Remove a value from the stack
public int pop();
// See the value on the "top" of the stack (next to be removed)
public int peek();
}
MyStack a = ...; // [ ]
a.push(1); // [ 1 ]
a.push(2); // [ 2 1 ]
a.peek(); // returns 2
a.push(3); // [ 3 2 1 ]
a.pop(); // [ 2 1 ], returns 3
a.push(4); // [ 4 2 1 ]
a.peek(); // returns 4
| Array | List | |
| Push | O(1)/O(n) | O(1) |
| Pop | O(1) | O(1) |
| Peek | O(1) | O(1) |
Stack<Integer> a = new Stack<Integer>();
a.push(1);
a.push(2);
System.out.println(a.pop()); // 2. remove and return top of stack.
a.push(3);
System.out.println(a); // [1, 3]
int stackSize = a.size();
boolean isEmpty = a.empty();
int peekTop = a.peek();Write a function to determine if a string consisting of the characters '{', '}', '[', and ']' is balanced.
For example, "{[]}" is balanced, and "{[}]" is not.
public static boolean isBalanced(String braces) {
Stack<Character> stack = new Stack<Character>();
for (int i = 0; i < braces.length(); i++) {
switch (braces.charAt(i)) {
case '{': stack.push('{');
break;
case '[': stack.push('[');
break;
case '}': if (stack.pop() != '{') { return false; }
break;
case ']': if (stack.pop() != '[') { return false; }
break;
}
}
return stack.isEmpty();
}
// First-in first-out data structure
public interface MyQueue {
// Add a value to the back of the queue
public void enqueue(int value);
// Remove a value from front of the queue
public int dequeue();
// See the value on the "front" of the queue (next to be removed)
public int peek();
}
MyStack a = ...; // [ ]
a.enqueue(1); // [ 1 ]
a.enqueue(2); // [ 1 2 ]
a.peek(); // returns 1
a.enqueue(3); // [ 1 2 3 ]
a.dequeue(); // [ 2 3 ], returns 1
a.enqueue(4); // [ 2 3 4 ]
a.peek(); // returns 2
| Array | List | |
| Enqueue | O(1)/O(n) | O(1) |
| Dequeue | O(1) | O(1) |
| Peek | O(1) | O(1) |
import java.util.Queue;
import java.util.ArrayDeque;
Queue<String> stack = new ArrayDeque<String>();
Given one queue and one stack, how do you reverse the stack?
Stack<Integer> stack = new Stack<Integer>();
Queue<Integer> queue = new ArrayDeque<Integer>();
stack.push(1);
stack.push(2);
stack.push(3);
System.out.println(stack); // [1, 2, 3]
while (!stack.isEmpty()) {
queue.add(stack.pop());
}
while (!queue.isEmpty()) {
stack.push(queue.remove());
}
System.out.println(stack); // [3, 2, 1]
An absolutely essential concept.
Supported operations:
- insert()
- delete()
- find()
Why is it so impressive? All of these operations can be done in constant O(1) time.
Think of a hash map like a really really big array.
array[0] = 1 // insert(): O(1)
array[1] = null // delete(): O(1)
x = array[2] // find(): O(1)
An array that, instead of integer indexes, has indexes that can be anything.
map["0"] -> 1
map["Adam Cannon"] -> 1004
map["BullsAndCows"] -> 9001
map["thisisareallylongstringthatistoocoolomgomgomgomgomgomgadiadiadilove"] -> 0
Insert, find, and delete are all O(1) now. That's it?
No. :( An infinite size array for infinite possible indexes is unreasonable.
As it turns out, however, there's a way to simplify anything (String, object, integer) into an integer
This is called the Hash function: maps an object (of some type) to an integer.
Example:
x % 10027
Hash function: maps an object (of some type) to an integer.
Example:
public int hash(String s) {
int hashVal = 0;
for (int i = 0; i < s.length(); i++) {
hashVal = s.charAt(i) + hashVal * 37;
}
return hashVal;
}
For insert():
- Take any thing
Xthat maps toY - Simplify
Xinto an integeriusing a hash function - Set
array[i] = Y
For find():
- Take any thing
Xthat you want to findYfor. - Simplify
Xinto an integeriusing the same hash function - Set
Y = array[i]
This is awesome!
Well, there are some problems with hash maps
- Requires a lot of extra memory and a good hash function to avoid collisions
- What is a "good" hash function?
- Finding max or min is kind of difficult
But in general: excellent for what it can do.
import java.util.HashSet;
import java.util.HashMap;
// ...
HashSet<String> set = new HashSet<String>();
set.add("dog");
set.add("cat");
set.add("fish");
System.out.println(set.contains("dog")); // true
System.out.println(set.contains("horse")); // false
HashMap<String, String> map = new HashMap<String, String>();
map.put("Jenny", "867-5309");
System.out.println(map.get("Jenny")); // 867-5309
//iteratiing without modifying key in the map
for(String key : map.keySet()){
System.out.println("Key: "+key+" Value: "+
map.get(key) );
if(map.get(key) == "NULL" ){
map.put(key, "");
}
}
//iterate and deleting key
Iterator<String> keyIter = map.keySet().iterator();
while(keyIter.hasNext()){
String key = keyIter.next();
if (map.get(key) == "NULL"){
keyIter.remove();
}
}
//get key with max values
int maxValKey = Collections.max(map.entrySet(), Map.Entry.comparingByValue()).getKey();
//building a frequency map
String[] A = new String[]{"dog", "cat", "cat"};
for (String w : A)
count.put(w, count.getOrDefault(w, 0) + 1);Implement a word counter (not case sensitive, and ignoring special characters).
Example:
"Gabba gabba hey, gabba gabba hey!" -> { "gabba": 4, "hey": 2 }
import java.util.HashMap;
public static HashMap<String, Integer> countWords(String document) {
HashMap<String, Integer> counts = new HashMap<String, Integer>();
for (String word : document.split(" ")) {
String key = word.toLowerCase().replaceAll("[^a-zA-Z]", "");
if (counts.containsKey(key)) {
counts.put(key, counts.get(key) + 1);
} else {
counts.put(key, 1);
}
}
return counts;
}
- How HashMap works in Java? With Animation!! whats new in java8 tutorial. Youtube link
Hashtables, HashSets, Dictionaries (Python)
Slight variations, but all revolve around the same idea of index simplification via a hash function for constant time insert, delete, and find.
If you are really interested, lookup how to resolve hash map collisions or textbook hash functions
- Java HashSet geeksforgeeks link
- Hash map with Key only. No duplicate are allows.
HashSet<String> h = new HashSet<String>();
// Adding elements into HashSet usind add()
h.add("India");
h.add("Australia");
System.out.println("List contains India or not:"+
`h.contains("India"));
// Removing items from HashSet using remove()
h.remove("Australia");
// Iterating over hash set items
Iterator<String> i = h.iterator();
while (i.hasNext())
System.out.println(i.next());public class Node {
public int value;
public Node left;
public Node right;
public Node(int value, Node left, Node right) {
this.value = value;
this.left = left;
this.right = right;
}
public Node(int value) {
this(value, null, null);
}
}
These are mad useful. Can represent hierarchical data: parse trees in NLP, database indexes, etc.
Fast Vocabulary
- Root – The top node in a tree.
- Parent – The converse notion of child.
- Siblings – Nodes with the same parent.
- Descendant – a node reachable by repeated proceeding from parent to child.
- Ancestor – a node reachable by repeated proceeding from child to parent.
- Leaf – a node with no children.
- Edge – connection between one node to another.
- Path – a sequence of nodes and edges connecting a node with a descendant.
- Level – The level of a node is defined by 1 + the number of connections between the node and the root.
- Height – The height of a node is the number of edges on the longest downward path between the root and a leaf.
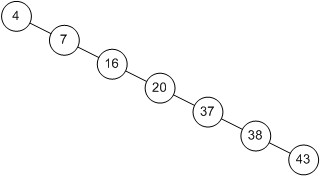
Binary Search Tree: every value in the left subtree of a node with a value is less than that value; every value in the right subtree of a node with a value is greater than that value.
This gives us O(log(n)) retrieval (in the average but not worst case; more on that later).
Before we move further...
public int fib(int n) {
if (n < 2) {
return 1;
} else {
return fib(n - 1) + fib(n - 2);
}
}
public boolean find(Node root, int value) {
if (root == null) {
return false;
}
if (value < root.value) {
return find(root.left, value);
} else if (value > root.value) {
return find(root.right, value);
} else {
return true;
}
}
Worst Case: Unbalanced Tree
We can traverse the tree in one of a few ways.
FBADCEGIH
We can traverse the tree in one of a few ways.
ABCDEFGHI
We can traverse the tree in one of a few ways.
ACEDBHIGF
How do we do a level-order traversal of a tree?
public void levelOrder(Node root) {
Queue<Node> queue = new Queue<Node>();
queue.add(root);
while (!queue.isEmpty()) {
Node curr = queue.remove();
System.out.println(curr.value);
if (curr.left != null) {
queue.add(curr.left);
}
if (curr.right != null) {
queue.add(curr.right);
}
}
}
A Priority Queue is an ADT is a list where each element has a "priority" associated with it.
Operations:
insert_with_priority()pull_highest_priority_element()
The maximally efficient way to implement this ADT is with a heap (O(log n) performance for both operations)
Heap Property: Parents are always more important than their children
To add an element: insert and reorder the tree (O(log n))
To pull the highest priority element: pop the root out and reorder the tree (O(log n))
class customeObj implements Comparable<customeObj>{
int field;
public customeObject(int field){}
@Override
//usage for max heap
public int compareTo(customeObj other)
if(this.field > other.field)
return 1;
else if(this.field < other.field)
return -1;
else return 0;
}
}
PriorityQueue<customeObj> maxHeap = new PriorityQueue<customeObj>(Collections.reverseOrder());
PriorityQueue<String> minHeap= new PriorityQueue<String>(){
@Override
public int compare(String s1, String s2) {
return s1.length() - s2.length();
}
};
customeObj athe = maxHeap.poll();
customeObj maxObj = maxHeap.peek();
int maxHeapSize = maxHeap.size();
maxHeap.add(new customeObj(3));AVL Trees (Trees that always stay balanced using rotation)
Red-Black Trees (Trees that always stay balanced using colors (fun!))
B-Trees (Trees designed for lots of data)
ADT consisting of Nodes and Edges
Basic operations:
adjacent(G, x, y): tests whether there is an edge from node x to node y.neighbors(G, x): lists all nodes y such that there is an edge from x to y.add(G, x, y): adds to G the edge from x to y, if it is not there.delete(G, x, y): removes the edge from x to y, if it is there.get_node_value(G, x): returns the value associated with the node x.set_node_value(G, x, a): sets the value associated with the node x to a.get_edge_value(G, x, y): returns the value associated to the edge (x,y).set_edge_value(G, x, y, v): sets the value associated to the edge (x,y) to v.
One way is to use an "adjacency list": We have a list of nodes and every node stores a list of adjacent nodes.
public class Node {
public int value;
public ArrayList<Edges> edges;
}
public class Edge {
public Node destination;
public int weight;
}
public class Graph {
public ArrayList<Node> nodes;
}
Say we have V nodes and E edges.
What is the performance for these operations?
- Add vertex
- Add edge
- Remove vertex
- Remove edge
Depends on implementation, but this is something you look up.
Problem: Given a node, can we reach this other node?
Search!
- Complexity: O(n)
- Space:O(h). Here
hrefering to the height of the tree. Corresponding to size of our stack call.
bool search(Node root, Node dest) {
if (root.value == dest.value)
return true;
root.visited = true;
for (Node n : root.adjacent) {
if (!n.visited) {
if (search(n, dest))
return true;
}
}
return false;
}- Complexity:
O(n) - Space:
O(m). here m refers to the maximum number of nodes at any level in the input tree.
bool search(Node root, Node dest) {
Queue q = new Queue();
if (root.value == dest.value)
return true;
root.visited = true;
q.enqueue(root);
while (!q.isEmpty()) {
Node r = q.dequeue();
for (Node n in r.adjacent) {
if (!n.visited) {
if (search(n, dest))
return true;
queue.enqueue(n);
}
}
}
return false;
}Interesting Graph Problems (wiki):
- Djikstra's
- Floyd-Warshall
- Ford-Fulkerson
- Kruskal's
The problem: given an array containing many values, permute the array so that those values are in order.
You'll definitely be expected to have a high-level understanding of these and know the runtimes. Maybe you'll have to implement one.
private static void swap(int[] array, int i, int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
Basically, find the minimum element n times.
public static void selectionSort(int array[]) {
for (int i = 0; i < array.length; i++) {
int minIndex = i;
for (int j = i; j < array.length; j++) {
if (array[j] < array[minIndex]) {
minIndex = j;
}
}
swap(array, i, minIndex);
}
}
General Information
- O(n^2) performance
- O(1) space
The maximum elements bubble to the top
public static void bubbleSort(int array[]) {
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array.length - 1; j++) {
if (array[j] > array[j + 1]) {
swap(array, j, j + 1);
}
}
}
}
General information
- O(n^2) performance
- O(1) space
- Split the array in half and sort each subarray.
- Weave the arrays back together in one fluid pass.
Here's where I'm going to stop implementing things and just explain them. Wikipedia is great.
Merge sort is recursive.
function mergeSort(A):
split A into A_beginning and A_end at the middle
mergeSort(A_beginning)
mergeSort(A_end)
return merge(A_beginning, A_end)
General Information
- O(n log n) performance
- O(n) space
##Sorting: Quicksort
"Divide and Conquer"
function quickSort(A):
pick a "pivot" element in A
move all elements less than the pivot to the beginning of A
move all elements greater than the pivot to the end of A
put the pivot in the middle
quicksort the beginning of A recursively
quicksort the end of A recursively
General Information
- O(n log n) performance
- Absolute worst case O(n^2) performance
Comparison-based sorts can't be faster than n * log(n). BUT non-comparison based ones can. There are catches, though.
public void countingSort(int[] array, int max) {
int[] counts = new int[max];
for (int i = 0; i < array.length; i++) {
counts[array[i] - 1]++;
}
int i = 0;
for (int j = 0; j < max; j++) {
while (counts[j] > 0) {
array[i++] = j + 1;
}
}
}
This is a prime example of how NOT to implement a hash map.
Anything slower than O(n^2) is not okay.
O(n^2) sorting algorithms are generally simpler, easier to code, and require less auxillary space
O(n log n) is the best comparison based sorting algorithm performance you can get (proven mathematically). These, however, tend to be more complicated and require more memory.
Faster than O(n log n) sorting sorting usually makes at least one huge assumption about our data set (e.g. counting sort)
You are given an unsorted array of size n. However, you are also told that where each element is in the unsorted array right now is at most k-1 positions away from its final correctly sorted position. You are told that 1 < k < n.
What is the best sorting strategy and what is our performance?
Solution (in Python):
import heapq
def better_sort(array, k):
final_array = []
heap = []
for x in xrange(k):
heapq.heappush(heap, array[x])
index = k
while heap:
final_array.append(heapq.heappop(heap))
if index < len(array):
heapq.heappush(heap, array[index])
index += 1
return final_array
Performance: O(n log k)
int number = 10;
String binInString = Integer.toBinaryString(number); //1010- https://www.youtube.com/watch?v=BXCEFAzhxGY
- 2 step. Step 1, Preprocessing. Idea: create a table
$\pi$ that encapsulate knowledges about how the pattern matches against shift of itself.
def prefix_function():
m = len(P)
pi = new array[1...m]
pi[1] = 0
l = 0
for r=2 -> m:
while l > 0 and P[l+1] != P[r]:
l = pi[l]
if P[l+1] == P[r]:
l += 1
pi[r] = l
return piJava Implementation
public int[] prefixTable(char[] P){
int[] pi = new int[P.length];
pi[0] = 0;
for(int l=0, r=1; r<pi.length; r++){
while(l != 0 && P[l] != P[r] )
l = pi[l-1];
if(P[l] == P[r] )
l += 1;
pi[r] = l;
}
return pi;
}- First Convert to base 10
- Conver to target base.
//area of a triangle
public computeTriangleArea(int[] P, int[] Q, int[] R){
return 0.5 * Math.abs(P[0]*Q[1] + Q[0]*R[1] + R[0]*P[1]
-P[1]*Q[0] - Q[1]*R[0] - R[1]*P[0]);
}-
How to code in your interview language
-
How to use Unix (scripting, regexes)
-
How a computer works (bits and bytes)
-
Object-oriented programming
int minInt = Integer.MIN_VALUE;
int maxInt = Integer.MAX_VALUE;
//double
double minDouble = Double.MIN_VALUE;// note. A **POSITIVE** number not _negative_
double maxDouble = Double.MAX_VALUE;//1.7*10^308
double _inf = Double.NEGATIVE_INFINITY;//-inf
double inf = Double.POSITIVE_INFINITY;//inf- Split String by space and punctuation
paragraph.split("[\\p{Punct}\\s]+")
https://github.com/adicu/interview_help
-
Cracking the Coding Interview
-
Google / Wikipedia
-
ICPC
-
CLRS